Bullet
Task number: 1994
A bullet with mass 10 g was fired against a stationery wooden block with mass 1 kg. It penetrated the block into depth 10 cm. If the wooden block was moveable, how deep would the bullet get? Assume that wood resists movement of the bullet steadily.
Given values
m = 10 g mass of the bullet M = 1 kg = 1 000 g mass of the block h1 = 10 cm depth into which the bullet penetrated the block h2 = ? depth into which the bullet would penetrate if the block was moveable Hint 1 – Laws of Conservation
Use the law of conservation of energy and momentum to solve this task.
Hint 2 – Immobile Block
What is going on with kinetic energy of the bullet in case the block is immobile? Write it down in an equation.
Hint 3 – Moveable Block
Write down the laws of conservation of momentum and energy for the freely moveable block.
HInt 4 – Desired Depth
You got three equations (1),(2),(3), now try to express the unknown depth h2.
Numerical Solution
m = 10 g mass of the bullet M = 1 kg = 1 000 g mass of the block h1 = 10 cm depth into which the bullet penetrated the block h2 = ? depth into which the bullet would penetrate if the block was moveable
\[h_{2}\,=\,\frac{h_{1}M}{m+M}\] \[h_{2}\,=\,\frac{10\,\cdot\,1\,000}{10\,+\,1\,000}\, \mathrm{cm}\] \[h_{2}\,\dot=\,9.9\,\mathrm{cm}\]Answer
If the block was moveable, the bullet would penetrate into depth \[h_{2}=\frac{h_{1}M}{m+M}=9.9\,\mathrm{cm}\] .
Complete Solution
We shall use the law of conservation of energy and momentum to solve this task.
Law of conservation of momentum:
Sum of individual momenta of objects in an isolated system remains constant, in other words, the total momentum of a system is conserved.
Law of conservation of energy:
Total energy of an isolated system is conserved.
Immobile block:
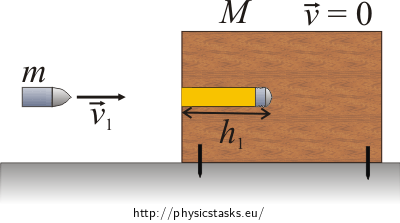
Kinetic energy of the bullet before hitting the block is equal to work done by resistance force F during its hindering on a path h1. Kinetic energy of the bullet gets transformed into inner energy of the wood and bullet, which manifests itself by increase in their temperamenture.
\[\frac{1}{2}mv_{1}^{2}\,=\,Fh_{1}\] \[F\,=\,\frac{mv_{1}^{2}}{2h_{1}}\tag{1}\]F … resistance force
m … mass of the bullet
v1 … speed of the bullet
h1 … depth into which the bullet penetrated the immobile block
Freely moveable block:
In case of freely moveable block it holds:
\[\mathrm{ZZH:} \qquad \vec p_{1}+ \vec p_{2}\,=\, \vec p_{1}^{'}+ \vec p_{2}^{'}\,,\]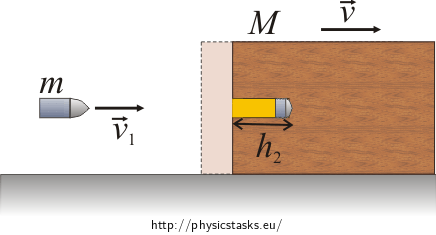
where
\(\vec p_{1}\)… vector of momentum of the bullet before impact\(\vec p_{2}\)… vector of momentum of the block before impact\(\vec p_{1}^{'}\)… vector of momentum of the bullet after impact\(\vec p_{2}^{'}\)… vector of momentum of the block after impact\[m\vec v_1+0\,=\,(M+m)\vec{v}\]In scalars:
\[mv_1\,=\,(M+m)v\,,\tag{2}\]where
m… mass of the bullet
v1… speed of the bullet before impact
M… mass of the block
v… resulting speed of the system formed by the bullet and block
\[Law of conservation of energy:\]The bullet penetrates into depth labeled as h2 and then the block with bullet will be moving with speed v. Initial kinetic energy of the bullet gets transformed both into kinetic energy of the block and bullet and into work of resistance force which manifests itself by increase in their temperature.
\[\frac{1}{2}mv_{1}^{2}\,=\,Fh_{2}+\frac{1}{2}(m+M)v^{2}\,,\tag{3}\]where F… resistance force
h2… depth into which the bullet penetrated when the block was moveable
We express the final speed of the system from equation (2):
\[v\,=\,\frac{mv_{1}}{m\,+\,M}\,.\tag{4}\]We input gained expressions for final speed (4) and for resistance force (1).
\[\frac{1}{2}mv_{1}^{2}\,=\,\frac{mv_{1}^{2}}{2h_{1}}h_{2}\,+\,\frac{1}{2}(m\,+\,M)\frac{m^{2}v_{1}^{2}}{\left(m\,+\,M\right)^{2}}\,.\]Multiply both sides of equation by two:
\[mv_{1}^{2}\,=\,\frac{mv_{1}^{2}}{h_{1}}h_{2}\,+\,(m\,+\,M)\frac{m^{2}v_{1}^{2}}{\left(m\,+\,M\right)^{2}}\,.\]We know that speed before hitting the block v1 is nonzero, therefore we can divide by it the equation.
We get:
\[m\,=\,\frac{m}{h_{1}}h_{2}\,+\,\left(m\,+\,M\right)\frac{m^{2}}{(m\,+\,M)^{2}}\,.\]We modify to get:
\[m\,=\,\frac{m}{h_{1}}h_{2}\,+\,\frac{m^{2}}{\left(m\,+\,M\right)}\,.\]Then we divide by the mass of the bullet:
\[1\,=\,\frac{h_{2}}{h_{1}}\,+\,\frac{m}{\left(m\,+\,M\right)}\,.\]Next we multiply the equation by h1:
\[h_{1}\,=\,h_{2}\,+\,\frac{h_{1}m}{m\,+\,M}\,.\]Take the fraction \[\frac{h_{1}m}{m\,+\,M}\] on the other side and factor h1 out of the parantheses.
\[h_{2}\,=\,h_{1}\left(1\,-\,\frac{m}{m\,+\,M}\right)\,.\]Now we reduce to have a common denominator:
\[h_{2}\,=\,h_{1}\left(\frac{m\,+\,M\,-\,m}{m\,+\,M}\right)\,=\,\frac{h_{1}M}{m\,+\,M}\,.\] \[h_{2}\,=\,\frac{10\,\cdot\,1\,000}{10\,+\,1\,000}\,\mathrm{cm}\] \[h_{2}\,\dot=\,9.9\,\mathrm{cm}\]Answer: If the block was moveable, the bullet would penetrate into depth 9.9 cm.




