An ant on a rod
Task number: 384
A slim rod OA of length R rotates with angular velocity ω in a clockwise direction in a plane around point O. There is an ant crawling along the rod from the point O to the point A with constant speed \(\vec{v}(t)\) (measured with regard to the rod). Determine the time dependent location of the ant in the laboratory reference frame. Assume its position at time t = 0 s was at the centre of the rod.
Hint 1: A picture
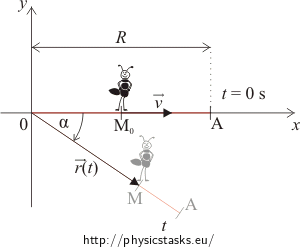
Let’s put point O of the rod at the origin of the coordinate system and let the rod begin at the x-axis at time t = 0 s. Draw a picture including the starting positions of the rod and the ant and also their positions at some random time t. Mark the position vector \(\vec r\) of the ant at time t.
Hint 2: Position vector of an ant
What is the distance the ant crawled in time t and what is the length of the position vector of the ant at time t? What is the angle the rod has turned in time t?
Using the angle α determine the x and y components of the position vector \(\vec{r}\left(t\right)\).
Complete solution
Picture:
Let’s split the motion into two parts; a uniform linear motion with velocity v and a rotary motion with angular velocity ω:
The ant has crawled a distance along the rod of vt.
The length of the position vector at time t is therefore (since the ant began at the centre of the rod):
\[r(t)=vt+\frac{R}{2}\tag{1}\]The rod has reached an angle:
\[\alpha=\omega{t}\]The length of the position vector changes with time according to equation (1):
\[r(t)=vt+\frac{R}{2}\]The x component of the position vector therefore equals
\[x(t)=r(t)\cos\alpha=\left(vt+\frac{R}{2}\right)\cos\omega{t}\]The y component of the position vector equals
\[y(t)=-r(t)\sin\alpha=-\left(vt+\frac{R}{2}\right)\sin\omega{t}\]Expressing the position vector as the vector sum of its components:
\[\vec{r}(t)= x(t)\vec{i} + y(t)\vec{j}\]where\(\vec{i}\), \(\vec{j}\) are unit vectors in directions x and y
\[\vec{r}(t)= \left(vt+\frac{R}{2}\right)\cos\left(\omega{t}\right)\vec{i}-\left(vt+\frac{R}{2}\right)\sin\left(\omega{t}\right) \vec{j}\]Answer
The time dependent position vector of the ant is:
\[\vec{r}(t)= \left(vt+\frac{R}{2}\right)\cos\left(\omega{t}\right)\vec{i}-\left(vt+\frac{R}{2}\right)\sin\left(\omega{t}\right) \vec{j}\]where \(\vec{i}\), \(\vec{j}\) are unit vectors in the corresponding directions x and y.
Visualisation of the movement
The folowing aplet should help with visualisation of the movement of an ant on a rod. Position of the ant in a given time is described by the position vector \(\vec{r}_{(t)}\), which we derived earlier. Clicking on the button „Start animation“, the animation of the movement will start, when the button is clicked again, the animation will stop. Time \(t\) can be changed on the slider. Button „Show the ant’s trace“ will turn the trace of the point M on, or off. Button „Show the ant’s trajectory“ will draw the trajectory of the point M. The „Reset“ button will stop the animation and return the aplet to it’s initial state.
Thanks to the aplet, we can easily see, that the trajectory of this particular ant is a spiral.