Skater
Task number: 1522
A skater of mass 70 kg stands on the glassy ice. He puts himself in motion by firing horizontally a ball of mass 3 kg at the speed 8 m s-1. How far will the skater move after firing the ball? A coefficient of friction between the ice and the skates f = 0.02.
Notation
M = 70 kg Mass of the skater m = 3 kg Mass of the ball v1 = 8 m s-1 Speed of the ball f = 0.02 Coefficient of friction between ice and skates sz = ? (m) Distance between the initial and the final position of the skater Analysis
At first we will find the velocity of the skater after firing the ball. For solving that we will use Conversation of Momentum. Then, we will solve what is the stopping distance of the skater when he is affected by the constant frictional force. We can use Law of Conservation of Energy or Newton’s laws.
Hint 1 – The Momentum of a System the skater + the ball
What do we know about the system the skater + the ball before and immediately after firing the ball? Draw a picture of the situation. In what direction the skater and the ball will move?
Hint 2 – Motion of the skater, work of the frictional force
What type of motion does the skater make when he is affected by the frictional force? What work does the frictional force do during the time when the skater is slowing down? What is this work equal to? What happens to the initial kinetic energy of the skater?
Numerical solution
We know:
\[m\,=\,3\,\mathrm{kg}\] \[M\,=\,70\,\mathrm{kg}\] \[v_1\,=\,8\,\mathrm{m\,s^{-1}}\] \[f\,=\,0.02\] \[g\,=\,9.81\,\mathrm{m\,s^{-2}}\]We look for:
\[s_z\,=\,?\] \[s_z\,=\,\frac{m^2v_1^2}{2fM^2g}\] \[s_z\,=\,\frac{3^2{\cdot}8^2}{2{\cdot}0{,}02{\cdot}70^2{\cdot}9{,}81}\,\mathrm{m}\] \[s_z\,=\,0.3\,\mathrm{m}\]Answer
The skater covers a distance of \(s_z\,=\,\frac{m^2v_1^2}{2fM^2g}\,=\,0.3\,\mathrm{m}.\)
Total Solution
At first we will find the velocity of the skater after firing the ball. For solving that we will use a Conversation of Momentum. Then, we will solve what is the stopping distance of the skater when he is affected by the constant frictional force. We can use the Law of Conservation of Energy or Newton’s laws.
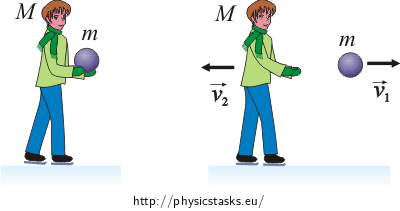
\(m\)…mass of the ball
\(M\)…mass of the skater
\(\vec{v_1}\)…velocity vector of the ball after firing the ball
\(\vec{v_2}\)…velocity vector of the skater after firing the ball
The initial Momentum of the System the skater + the ball was zero. According to the Conservation of Momentum the final momentum of the system after firing the ball has to be zero too. After firing the ball the skater will move in the opposite direction than the ball.
\[\vec{p_1}+\vec{p_2}\,=\,0\]\(\vec{p_1}\)…momentum vector of the ball after firing the ball
\(\vec{p_2}\)…momentum vector of the skater after firing the ball
\[m\vec{v_1}+M\vec{v_2}\,=\,0\]While both vectors are in the same direction, we can write a scalar equation:
\[mv_{1}-Mv_{2}\,=\,0\]The speed of the skater after firing the ball is:
\[v_{2}\,=\,\frac{mv_{1}}{M}\tag{1}\]The constant frictional force exerts on the skater against his direction.
\[F_t\,=\,Mgf\tag{2}\]\(F_t\)…frictional force
\(f\)…coefficient of friction
\(g\)…gravity of Earth
That is why the skater is slowing down with uniform acceleration.
Frictional force exerted on the skater while he is slowing down does the work:
\[W\,=\,F_ts_z\]\(W\)…work of frictional force
\(s_z\)…distance required to bring the skater to a halt
This work is equal to initial kinetic energy of the skater.
\[W\,=\,E_k\]Ek…initial energy of skater
\[F_ts_z\,=\,\frac{1}{2}Mv_2^2\] \[Mgfs_z\,=\,\frac{1}{2}Mv_2^2\] \[s_z\,=\,\frac{Mv_2^2}{2Mfg}\,=\,\frac{v_2^2}{2fg}\]We substitute speed v2 from the equation (1):
\[s_z\,=\,\frac{m^2v_1^2}{2fM^2g}\] \[s_z\,=\,\frac{3^2{\cdot}8^2}{2{\cdot}0.02{\cdot}70^2{\cdot}9.81}\,\mathrm{m}\] \[s_z\,=\,0.3\,\mathrm{m}\]The initial kinetic energy of the skater converts during slowing down into internal energy of skates and ice. It means that both will be heated.
Answer:The skater covers a distance of \(s_z\,=\,0.3\,\mathrm{m}\).
Note:
The distance can be solved using Newton’s second law and kinematic equations of uniformly accelerated motion.
Equation of motion of the skater:
\[\vec{F_t}+\vec{N}+\vec{F_g}\,=\,M\vec{a}\]\(\vec{F_t}\)…frictional force
\(\vec{N}\)…force of the ice perpendicular to the skater
\(\vec{F_g}\)…weight force
\(M\)…mass of the skater
\(\vec{a}\)…acceleration of the skater
Scalar equation:
\[-F_t\,=\,Ma\] \[N-F_g\,=\,0\]Let’s express the acceleration a of the skater:
\[a\,=\,\frac{-F_t}{M}\,=\,-gf\]Integrating the acceleration of the skater we will find the dependence of velocity on the time after firing the ball:
\[v\,=\,\int{a\mathrm{d}t}\,=\, -gft + K\tag{3}\] We find the constant K from the initial conditions. At time t = 0 s the skater had velocity v = v2 therefore: \[v_2 \,=\, 0 + K\] \[v \,=\, v_2-gft\]Integrating the velocity of the skater we will find the dependence of distance on the time after firing the ball:
\[s\,=\,\int{v\mathrm{d}t}\,=\,\int{(v_2-gft)\mathrm{d}t}\,=\,v_2t-\frac{1}{2}gft^2+C\]We find the constant C from the initial conditions. At time t = 0 s the skater was at zero position s = 0 m therefore:
\[0\,=\,0+C\] \[s\,=\,v_2t-\frac{1}{2}gft^2\]At the time of the final position tz the velocity is zero v = 0:
\[0\,=\,v_2-gft_z\]We express time of final position from there: tz:
\[t_z\,=\,\frac{v_2}{gf}\]We find the distance covered by the skater to the final position by inserting the time to the equation for the distances:
\[s_z\,=\,v_2t_z-\frac{1}{2}gft_z^2\] \[s_z\,=\,\frac{v_2^2}{gf}-\frac{v_2^2}{2gf}\] \[s_z\,=\,\frac{v_2^2}{2fg}\]



