Water streaming out of the tank
Task number: 1520
The tank has two holes drilled in the wall, first at a height h1 measured from the bottom and the second at a height h2. At what height h must be the water level in the tank, if we want the water jets to stream out of both holes to obtain the same range x? Air resistance is negligible.
At first solve the task generally then for values of h1 = 10 cm a h2 = 30 cm.
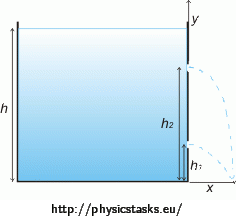
Notation
h1 = 10 cm height of the first hole (measured from the bottom) h2 = 30 cm height of the second hole (measured from the bottom) x = ? the range which the water jet obtains h = ? height of the water level in the tank Analysis
When solving the task we will use the knowledge of both fluid mechanics and horizontal throw. We express the the range which the water jet obtains in both cases. To do this, we need to know the velocity of the water discharge from both holes. We will find them using the Bernoulli equation.
Hint 1
How do we calculate the range \(x\) which the water jets obtains?
Hint 2
What else is valid for \(x_{1}\) and \( x_{2}\)?
Hint 3
How do we calculate the time \(t_{1}\), \(t_{2}\), in which the water falls to the ground?
Hint 4
How do we calculate the velocity \(v_{1}\) aand \(v_{2}\) of the water streaming out of the holes?
Hint 5
Use the relation (3), substitute the computed time and the velocities and express the level of water you are searching for.
Total Solution
Calculation of the distance where the water falls
We calculate the length \(x\) using this equation:
\[x=vt,\]where \(v\) is the velocity of the water at the moment of streaming out and \(t\) is a time, when the water travels to the distance \(x\).
First height
If the water streams out from height \(h_{1}\),:
\[x_{1}=v_{1}t_{1}.\tag{1}\]Second height
If the water streams out from height \(h_{2}\),:
\[x_{2}=v_{2}t_{2}.\tag{2}\]We want the water jets from both holes to travel to the same distance, which means:
\[x_{1}=x_{2}.\]We substitute for \(x_{1}\), \(x_{2}\) from equation (1), (2) and get:
\[v_{1}t_{1}=v_{2}t_{2}.\tag{3}\]Time calculation
Time \(t\), in which the water travels to the distance \(x\), we calculate from the equation:
\[y=\frac{1}{2}gt^2,\]where \(g\) is gravitational acceleration and \(y\) is the height from which the water steams out.
First height
If the water steams out from the height \(h_{1}\):
\[h_{1}=\frac{1}{2}gt^2_{1}.\]We divide both sides of the equation by \(\frac{1}{2}g\).
\[\frac{2h_{1}}{g}=t^2_{1}\]We extract both sides of the equation and became \(t_{1}\):
\[t_{1}=\sqrt{\frac{2h_{1}}{g}}.\tag{4}\]Second height
If the water steams out from the height \(h_{2}\):
\[h_{2}=\frac{1}{2}gt^2_{2}.\]We divide both sides of the equation by \(\frac{1}{2}g\).
\[\frac{2h_{2}}{g}=t^2_{2}\]
We extract both sides of the equation and get \(t_{2}\):
\[t_{2}=\sqrt{\frac{2h_{2}}{g}}.\tag{5}\]Velocity calculation
We calculate the velocity of water \(v\) using Bernoulli equation:
\[\frac{1}{2}\rho v^2_{i}+\rho g h_{i}+p_{i}=\frac{1}{2}\rho v^2_{e}+\rho gh_{e}+p_{e},\]where \(\rho\) is water density, \(p\) is a pressure and \(h\) is a height above the ground. Index \(i\) means inside the tank and index \(e\) outside.
The velocity of the water at the place where it streams out is zero for both holes inside the tank, so:
\[\frac{1}{2}\rho v^2_{i}=0.\]The height above the ground is the same both outside and inside, so the part \(\rho gh\) corresponding to the potential energy is eliminated. The pressure at the discharge inside the tank is determined by the sum of the atmospheric pressure \(p_{a}\) and the hydrostatic pressure of the water column above the discharge \(p_{h}=(h-h_{i})\rho g\). Thus:
\[p_{i}=p_{a}+(h-h_{i})\rho g .\]The pressure at the discharge of the tank is for both holes equal to atmospheric pressure. We rewrite Bernoulli equation for both cases.
First height
If the water streams out from the height \(h_{1}\):
\[ p_{a}+\rho g( h- h_{1})=\frac{1}{2} \rho v^2_{1}+p_{a}.\]We subtract \(p_{a}\) from both sides of the equation and divide by \(\rho\):
\[ g( h- h_{1})=\frac{1}{2} v^2_{1}.\]We multiply both sides by \(2\) and extract them:
\[ v_{1}=\sqrt{2g( h- h_{1})}.\tag{6}\]Second height
If the water streams out from the height \(h_{2}\):
\[ p_{a}+\rho g( h- h_{2})=\frac{1}{2} \rho v^2_{2}+p_{a}.\]We subtract \(p_{a}\) from both sides of the equation and divide by \(\rho\):
\[ g( h- h_{2})=\frac{1}{2} v^2_{2}.\]We multiply both sides by \(2\) and extract them:
\[ v_{2}=\sqrt{2g( h- h_{2})}.\tag{7}\]Substitution to the relation (3)
We substitute \(t_{1},t_{2},v_{1},v_{2}\) to the relation (3) from relations (4),(5), (6) and (7).
\[v_{1}t_{1}=v_{2}t_{2}\] \[\sqrt{2g( h- h_{1})}\sqrt{\frac{2h_{1}}{g}}=\sqrt{2g( h- h_{2})}\sqrt{\frac{2h_{2}}{g}}\]We modify both sides of equation by squaring them:
\[2g( h- h_{1})\frac{2h_{1}}{g}= 2g( h- h_{2})\frac{2h_{2}}{g}.\]\(g\) is canceled out and we divide both sides od equation by \(4\):
\[( h- h_{1})h_{1}=( h- h_{2})h_{2}.\]We multiply the terms in brackets, terms with \(h\) we move to the left side and the rest to the right side of the equation:
\[hh_{1}-hh_{2}=h^2_{1}-h^2_{2}.\]We factor out \(h\) and the term \(h^2_{1}-h^2_{2}\) we rewrite as a product:
\[h(h_{1}-h_{2})=(h_{1}-h_{2})(h_{1}+h_{2}).\]We cancel out \((h_{1}-h_{2})\) and get:
\[h=h_{1}+h_{2}.\tag{8}\]Numerical solution
We substitute the given values \(h_{1}=10\,\mathrm{cm}\) and \(h_{2}=30\,\mathrm{cm}\) to the relation (8).
\[h=h_{1}+h_{2}=10\,\mathrm{cm}+30\,\mathrm{cm}=40\,\mathrm{cm}\]Answer
Water from both holes will travel to the same distance if the water level is at height \(h\) according to this relation:
\(h=h_{1}+h_{2}.\)For given values \(h_{1}=10\,\mathrm{cm}\) a \(h_{2}=30\,\mathrm{cm}\) :
\(h=40\,\mathrm{cm}.\)




