Rowboats
Task number: 1754
There are two rowboats (boat 1 and boat 2) at rest with their sterns together. There are two boys, each sitting in one boat. The boy in boat 1 of total mass m1 is pushing himself away from boat 2 of total mass m2 using a paddle and applying a constant force for time Δt. Boat 2 gets accelerated to speed v2.
a) Determine the speed v at which the two boats are moving away from each other.
b) Determine the magnitude of force F applied by the boy.
c) Determine the change of distance Δs between the boats when the boy was applying the force.
d) Determine the work W done while the boy was pushing.
e) Determine the ratio between the kinetic energies of the two boats.
Neglect all resistive forces. First find the general solution and then find the solution for the following values:
m1 = 240 kg, m2 = 160 kg, v2 = 0.90 m·s-1, Δt = 1.5 s.
Notation
m1 = 240 kg mass of boat 1 m2 = 160 kg mass of boat 2 v2 = 0.90 m·s-1 speed of boat 2 Δt = 1.5 s duration for which the boy in boat 1 pushes v = ? (m·s-1) mutual speed of the boats F = ? (N) force applied by the boy Δs = ? (m) change of distance between the boats when the boy was applying the force W = ? (J) work done while the boy was pushing \(\frac{E_{k2}}{E_{k1}}\) = ?
ratio between the kinetic energies of the two boats Hint a – Momentum Conservation Principle
Draw a picture of the situation. Using the momentum conservation principle (MCP) determine the speed of boat 1. How can you determine the mutual speed of the boats?
Hint b – Magnitude of the Acting Force
The boy is applying a constant force F for time Δt to boat 2. While he is applying the force, the momentum of boat 2 changes by Δp. Try to write that down using Newton’s second law of motion.
Hint c – Change of Distance of the Boats
What motion do the boats perform relative to the water surface while being pushed? What distance do they cover while being pushed?
Hint d – Work Done
What does the work done during the pushing turn into? Express it with an equation.
Hint e – Ratio Between the Kinetic Energies
Express the ratio of the kinetic energy Ek2 of boat 2 to the kinetic energy Ek1 of boat 1.
Numerical calculation:
It is given:
\[m_1\,=\,240\,\mathrm{kg},\] \[m_2\,=\,160\,\mathrm{kg},\] \[v_2\,=\,0.9\,\mathrm{m \cdot s^{-1}},\] \[\Delta t\,=\,1.5\,\mathrm{s}.\]a) We are solving for:
\[v\,=\,?,\] \[v\,=\,\frac{m_1+m_2}{m_1}v_2,\] \[v\,=\,\frac{240+160}{240}\cdot 0.9\,\mathrm{m \cdot s^{-1}},\] \[v\,=\,1.5\,\mathrm{m \cdot s^{-1}}.\]b) We are solving for:
\[F\,=\,?,\] \[F\,=\,\frac{m_2v_2}{\Delta t},\] \[F\,=\,\frac{240{\cdot}0.9}{1.5}\,\mathrm{N},\] \[F\,=\,96\,\mathrm{N}.\]c) We are solving for:
\[\Delta s\,=\,?,\] \[\Delta s\,=\, \frac {m_1+m_2}{2m_1}v_2\Delta t,\] \[\Delta s\,=\, \frac {240+160}{2{\cdot}240}\cdot0.9{\cdot}1.5\,\mathrm{m},\] \[\Delta s\,=\, 1.1\,\mathrm{m}.\]d) We are solving for:
\[W\,=\,?,\] \[W\,=\,\frac{m_2(m_1+m_2)}{2m_1}v_2^2,\] \[W\,=\,\frac{160\cdot(240+160)}{2{\cdot}240}\cdot0.9^2\,\mathrm{J},\] \[W\,=\,108\,\mathrm{J}.\]e) We are solving for:
\[\frac{E_{k2}}{E_{k1}}\,=\,?,\] \[\frac{E_{k2}}{E_{k1}}\,=\,\frac{m_1}{m_2},\] \[\frac{E_{k2}}{E_{k1}}\,=\,\frac{240}{160},\] \[\frac{E_{k2}}{E_{k1}}\,=\,\frac{3}{2}.\]Answer
a) The magnitude of the mutual speed of the boats is: \[v\,=\,\frac{m_1+m_2}{m_1}v_2\,=\,1.5\,\mathrm{m \cdot s^{-1}}.\]
b) The magnitude of the force applied by the boy in boat 1 to boat 2 is: \[F\,=\,\frac{m_2v_2}{\Delta t}\,=\,96\,\mathrm{N}.\]
c) The change in distance of the boats during the pushing of the boy in boat 1 is: \[\Delta s\,=\, \frac {m_1+m_2}{2m_1}v_2\Delta t\,=\, 1.1\,\mathrm{m}.\]
d) Work done during the pushing is: \[W\,=\,\frac{m_2(m_1+m_2)}{2m_1}v_2^2\,=\,108\,\mathrm{J}.\]
e) The ratio of the kinetic energy of boat 2 to the kinetic energy of boat 1 is: \[\frac{E_{k2}}{E_{k1}}\,=\,\frac{m_1}{m_2}\,=\,\frac{3}{2}.\]
Complete Solution of a)
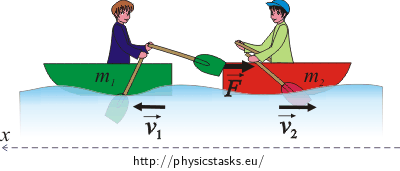
From the momentum conservation principle we know that the momentum of the boats before the pushing has to be equal to the momentum of the boats after they are pushed.
\[\mathrm{MCP}: \qquad \vec{p_{01}}+\vec{p_{02}}=\vec{p_1}+\vec{p_2}\]\(\vec{p_{01}}\)… momentum of boat 1 and the boy in it before being pushed (p01 = 0)
\(\vec{p_{02}}\)… momentum of boat 2 and the boy in it before being pushed (p02 = 0)
\(\vec{p_1}\)…momentum of boat 1 and the boy in it after being pushed
\(\vec{p_2}\)…momentum of boat 2 and the boy in it after being pushed
\[0=m_1\vec{v_1}+m_2\vec{v_2}\]\(m_1\)…mass of boat 1 with the boy in it
\(m_2\)…mass of boat 2 with the boy in it
\(v_1\)…speed of boat 1 with the boy in it
\(v_2\)…speed of boat 2 with the boy in it
Let us assume that the boats move in a straight line. We will write the equation in scalar form:
\[m_1v_1-m_2v_2\,=\,0.\]We will evaluate speed v1:
\[v_1\,=\,\frac{m_2v_2}{m_1},\tag{1}\]The boats are moving away from each other so we get their mutual speed by adding their speeds together.
\[v\,=\,v_1+v_2\]\(v\)…mutual speed of the boats
We will substitute v1 from equation (1):
\[v\,=\,\frac{m_2v_2}{m_1}+v_2,\] \[v\,=\,\frac{m_1+m_2}{m_1}v_2.\tag{2}\] \[v\,=\,\frac{240+160}{240}\cdot0.9\,\mathrm{m \cdot s^{-1}},\] \[v\,=\,1.5\,\mathrm{m \cdot s^{-1}}.\]Answer: The magnitude of the mutual speed of the boats is \(v\,=\,1.5\,\mathrm{m \cdot s^{-1}}.\)
Complete Solution of b)
In our situation, we can write Newton’s second law of motion in the following form:
\[F\,=\,\frac{\Delta p}{\Delta t},\]\(F\)…the force that is being applied by the boy in boat 1 to boat 2,
\(\Delta t\)…the duration for which the boy is applying the force F to boat 2,
\(\Delta p\)…the change of momentum of boat 2,
\[\Delta p\,=\,m_2v_2-0,\] \[F\,=\,\frac{m_2v_2}{\Delta t},\] \[F\,=\,\frac{240{\cdot}0.9}{1.5}\,\mathrm{N},\] \[F\,=\,96\,\mathrm{N}.\]Answer: The magnitude of the force applied by the boy in boat 1 to boat 2 is \(F\,=\,96\,\mathrm{N}.\)
Complete Solution of c)
The boats are in a uniformly accelerated motion relative to the water surface while being pushed.
Boat 1 covers a distance s1:
\[s_1\,=\,\frac{1}{2}a_1(\Delta t)^2.\]We can express the acceleration a1 as:
\[a_1\,=\,\frac{v_1}{\Delta t},\] \[s_1\,=\,\frac{1}{2}v_1\Delta t.\]Boat 2 covers a distance s2:
\[s_2\,=\,\frac{1}{2}a_2(\Delta t)^2.\]We can express the acceleration a2 as:
\[a_2\,=\,\frac{v_2}{\Delta t},\] \[s_2\,=\,\frac{1}{2}v_2\Delta t.\]In total the boats move away from each other during the pushing by a distance Δs:
\[\Delta s\,=\, s_1+s_2\,=\,\frac{1}{2}v_1\Delta t+\frac{1}{2}v_2\Delta t.\]We can substitute for the speed v1 from equation (1):
\[\Delta s\,=\,\frac{1}{2}\frac{m_2v_2}{m_1}\Delta t+\frac{1}{2}v_2\Delta t,\] \[\Delta s\,=\,\frac{m_1+m_2}{2m_1}v_2\Delta t, \] \[\Delta s\,=\, \frac {240+160}{2{\cdot}240}\cdot0.9{\cdot}1.5\,\mathrm{m},\] \[\Delta s\,=\, 1.1\,\mathrm{m}.\]The situation can also be solved in a system centered for example on boat 1.
In this system boat 2 is moving away from boat 1 in a uniformly accelerated motion and in time Δt it reaches a final speed v. The change of distance is:
\[\Delta s\,=\,\frac{1}{2}v\Delta t,\]\(\Delta s\)…change of distance between the boats
We will substitute the speed v from equation (2):
\[\Delta s\,=\, \frac {m_1+m_2}{2m_1}v_2\Delta t.\tag{3}\]Answer: The change in distance of the boats during the pushing of the boy in boat 1 is \(\Delta s\,=\, 1.1\,\mathrm{m}.\)
Complete Solution of d)
The work done during the pushing causes an increase in the kinetic energies of the boats. (We neglect the changes of internal energy.)
\[W\,=\,E_{k1}+E_{k2}\]\(W\)…Work done
\(E_{k1}\)…kinetic energy of boat 1 with the boy in it
\(E_{k2}\)…kinetic energy of boat 2 with the boy in it
\[W\,=\,\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2\]We will substitute the speed v1 from equation (1):
\[W\,=\,\frac{1}{2}m_1\frac{m_2^2v_2^2}{m_1^2}+\frac{1}{2}m_2v_2^2,\] \[W\,=\,\frac{m_2^2v_2^2}{2m_1}+\frac{m_2v_2^2}{2},\] \[W\,=\,\frac{m_2(m_1+m_2)}{2m_1}v_2^2,\] \[W\,=\,\frac{160\cdot(240+160)}{2{\cdot}240}\cdot0.9^2\,\mathrm{J},\] \[W\,=\,108\,\mathrm{J}.\]Answer: Work done during the pushing is \(W\,=\,108\,\mathrm{J}.\)
Complete Solution of e)
The ratio of the kinetic energy Ek2 to the kinetic enrgy Ek1 is:
\[\frac{E_{k2}}{E_{k1}}\,=\,\frac{\frac{1}{2}m_2v_2^2}{\frac{1}{2}m_1v_1^2},\] \[\frac{E_{k2}}{E_{k1}}\,=\,\frac{m_2v_2^2}{m_1\frac{m_2^2v_2^2}{m_1^2}},\] \[\frac{E_{k2}}{E_{k1}}\,=\,\frac{m_1}{m_2},\] \[\frac{E_{k2}}{E_{k1}}\,=\,\frac{240}{160},\] \[\frac{E_{k2}}{E_{k1}}\,=\,\frac{3}{2}.\]Answer: The ratio of the kinetic energy of boat 2 to the kinetic energy of boat 1 is \(\frac{E_{k2}}{E_{k1}}\,=\,\frac{3}{2}\).


