Worker Dragging a Crate
Task number: 1983
A worker drags a crate across a smooth horizontal floor. The worker exerts a force of magnitude 210 N on the rope, which is inclined at an upward angle 20° to the horizontal. Determine the work performed by the following forces provided that the crate was moved by 0.5 m:
a) force exerted by the worker
b) gravitational force
c) normal force exerted by the floor on the crate.
d) What is the total work performed by all of the forces above?
Neglect the friction of the crate on the floor.
Given values
m = 50 kg Mass of the crate F = 210 N Magnitude of the force exerted by the worker on the crate α = 20° Angle formed by the force vector \(\vec{F}\) and the displacement vector s = 0.5 m Displacement W = ? Work performed by force \(\vec{F}\) Wg = ? Work performed by the gravitational force WN = ? Work performed by the normal force WC = ? Total work Hint 1 – Work performed by the worker
Draw a picture and mark all of the forces acting on the crate.
The force exerted by the worker can be considered constant. What is the relation for work performed by a constant force?
Hint 2 – Work performed by gravitational force
In the relation (1) for a constant force substitute the force \(\vec{F}\) by the relation for gravitational force. What is the angle between the gravitational force and the displacement vector?
Hint 3 – Work performed by normal Force
In the relation (1) substitute the force \(\vec{F}\) by the normal force \(\vec{N}\).
Hint 4 – Total work
The total work can be determined by the sum of works performed by individual forces.
Numerical solution
a)
\[F\,=\, 210\, \mathrm{N}\] \[s\,=\, 0.5 \,\mathrm{m}\] \[\alpha\,=\,20^{\circ}\]
\[W\,=\,Fs\cos\alpha\] \[W\,=\,210{\cdot}0.5\cdot\cos20^{\circ}\,\mathrm{J}\] \[W\,=\,105{\cdot}0.94\,\mathrm{J}\] \[W\,=\,98.7\,\mathrm{J}\dot=\, 99\,\mathrm{J}\]b)
The gravitational force vector forms an angle of 90° with the displacement vector. Therefore the work performed by this force is zero.
c)
The normal force vector forms an angle of 90° with the displacement vector. Therefore the work performed by this force is zero.
d)
\[W\,=\,98.7\,\mathrm{J}\] \[W_\mathrm{g}\,=\,0\,\mathrm{J}\] \[W_\mathrm{N}\,=\,0\,\mathrm{J}\] \[W_\mathrm{c}\,=\,W+W_\mathrm{g}+W_\mathrm{N}\] \[W_\mathrm{c}\,=\,98.7\,\mathrm{J} \dot=\, 99\,\mathrm{J}\]Answer
a) The work performed by the worker is \(W\,=\,Fs\cos\alpha\,\dot=\, 99\,\mathrm{J}\).
b) The work performed by the gravitational force is zero.
c) The work performed by the normal force is zero.
d) The total work is \(W_\mathrm{c}\,=\,W+W_\mathrm{g}+W_\mathrm{N}\,=\,Fs\cos\alpha\,\dot=\, 99\,\mathrm{J}\).
Comment
The motion of the crate is a uniformly accelerated motion.
In this task we solve an idealized problem, in which we do not take into account the frictional force, which would in a real situation act in the direction opposite to the force \(\vec{F}\).
Overall solution of a) – Work performed by the worker
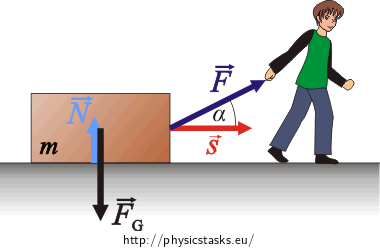
\(\vec{F}\) … force exerted by the worker on the crate
\(\vec{N}\) … normal force exerted by the floor
\(\vec{F}_\mathrm{g}\) … gravitational force
If the force acting on the body is constant, we determine the work performed by this force to be a product of the force vector and the displacement vector.
\[W\,=\,\vec{F}\cdot\vec{s}\]
\(W\) … performed work
\(\vec{F}\) … force vector exerted by the worker
\(\vec{s}\) … displacement vector
For the scalar product it holds:
\[W\,=\,Fs\cos \alpha.\tag{1}\] \[F= 210 \,\mathrm{N},\] \[s= 0{,}5\,\mathrm{m},\] \[\alpha=20^{\circ},\] \[W\,=\,Fs\cos\alpha\,=\,210{\cdot}0.5\cdot\cos20^{\circ}\,\mathrm{J}\,=\,105{\cdot}0.94\,\mathrm{J1},\] \[W\,=\,98.7\,\mathrm{J}\dot=\, 99\,\mathrm{J}.\]Answer: The work performed by the worker is \[W\,=\,Fs\cos\alpha\,\dot=\, 99\,\mathrm{J}.\]
Overall solution of b) – Work performed by the gravitational force
In the relation (1) we substitute the constant force \(\vec{F}\) by the relation for gravitational force \(\vec{F}_\mathrm{g}\).
\[W_\mathrm{g}\,=\,\vec{F}_\mathrm{g}\cdot\vec {s}\] \[W_\mathrm{g}\,=\,m\cdot\vec{g}\cdot\vec{s}\] \[W_\mathrm{g}\,=\,mgs\cos \alpha^{'}\]\(W_\mathrm{g}\) … work performed by the gravitational force
\(\vec{F}_\mathrm{g}\) … gravitational force
\(m\) … mass of the crate
\(\vec{g}\) … gravitational acceleration
\(\vec{s}\) … displacement vector
\(\alpha^{'}\) … angle formed by the vector of the gravitational force and the displacement vector, \(\alpha^{'}=90^{\circ}\)
\[\cos\alpha^{'}\,=\,\cos90^{\circ}\,=\,0\] \[W_\mathrm{g}\,=\,m\cdot g\cdot s\cdot 0\,=\,0\]Answer: The work performed by the gravitational force is zero.
Overall solution of c) – Work performed by the normal force
In the relation (1) substitute the force \(\vec{F}\) by the normal force \(\vec{N}\).
\[W_\mathrm{N}\,=\,\vec{N}\cdot\vec{s}\] \[W_\mathrm{N}\,=\,Ns\cos\alpha^{''}\]\(W_\mathrm{N}\) … work performed by the normal force
\(\vec{N}\) … normal force
\(\vec{s}\) … displacement vector
\(\alpha^{''}\) … angle formed by the vector of the normal force and the displacement vector
The normal force vector forms an angle of 90° with the displacement vector. The work is therefore zero.
\[\cos\alpha^{''}\,=\,\cos90^{\circ}\,=\,0\] \[W_\mathrm{N}\,=\,m\cdot g\cdot s\cdot 0\,=\,0\]Answer: The work performed by the normal force is zero.
Overall solution of d) – Total work
The total work can be determined the sum of works performed by individual forces
\[W_\mathrm{c}\,=\,W+W_\mathrm{g}+W_\mathrm{N}\]\(W_\mathrm{c}\) … total work
\(W\) … work performed by the force \(\vec{F}\)
\(W_\mathrm{g}\) … work performed by the gravitational force
\(W_\mathrm{N}\) … work performed by the normal force
\[W_\mathrm{c}\,=\,F\cdot s \cos\alpha\,+\,0\,+\,0\] \[W\,=\,Fs\cos\alpha\] \[W_\mathrm{g}\,=\,0\,\mathrm{J}\] \[W_\mathrm{N}\,=\,0\,\mathrm{J}\] \[W_\mathrm{c}\,=\,W+W_\mathrm{g}+W_\mathrm{N}=Fs\cos\alpha\] \[W_\mathrm{c}\,=\,98.7\,\mathrm{J}\dot=\, 99\,\mathrm{J}\]Answer: The total work is \(W_\mathrm{c}\,=\,W+W_\mathrm{g}+W_\mathrm{N}\,=\,Fs\cos\alpha\,\dot=\, 99\,\mathrm{J}\).




