Cottage Dwellers
Task number: 1990
The residents of an inlet have their cottages built near a river with width L. When neighbours want to meet, they use boats to travel.
Mr. Smith owns a boat that sails on still water with constant speed vb (speed refers to the magnitude of velocity). He decides to visit Mr. Jones with his neighbour, Mr. Brown.
Determine how long the journey will take if you know the following:
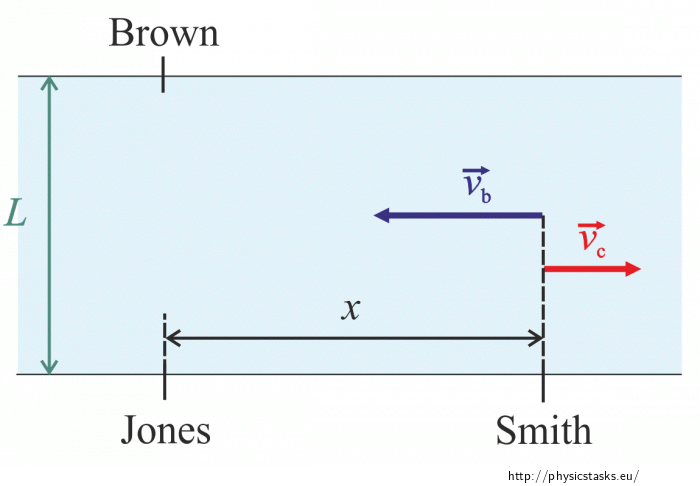
Mr. Smith will first go to Mr. Brown, who lives on the same side of the river, away at distance x against the current. Then, they will both sail to Mr. Jones, who lives on the other side of the river in a cottage exactly opposite Mr. Brown's cottage.
Assume the velocity of the current is constant and has a magnitude vr.
Solve for values: L = 200 m, vb = 2 m·s-1, vc = 1 m·s-1, x = 500 m.
Given values
L = 200 m river width vb = 2 m·s−1 boat speed on still water vc = 1 m·s−1 current speed x = 500 m distance between the houses of Mr. Smith and Mr. Brown t = ? (s) duration of the journey Hint 1: Time t1 from Mr. Smith to Mr. Brown
Determine the time t1 it takes for Mr. Smith to sail to Mr. Brown.
You know the distance of the journey. What is the velocity v1 with which Mr. Smith sails to Mr. Brown?
Draw a free body diagram describing the situation.
Hint 2 : Time t2 from Mr. Brown to Mr. Jones
Determine the time t2 it takes for Mr. Smith and Mr. Brown to sail to Mr. Jones.
Once again, you know the distance of the journey. In what direction do they sail? Can they head straight to Mr. Jones's cottage?
What is the speed v2 with which they sail? Draw a free body diagram.
Hint 3: Total duration t of the journey
What holds for the total duration of the journey t? Can you express it using previous calculations?
OVERALL SOLUTION
First we will determine the time t1 it will take Mr. Smith to sail to Mr. Brown and then the time t2 it will take them to sail to Mr. Jones.
\[t=t_1+t_2.\]
Time t1 from Mr. Smith to Mr. Brown
Figure 1:
Speed of the boat v1 in relation to the shore is, if it sails against the current, equal to the difference between the speed of the boat on still water vb and the speed of the current vc:
\[v_\mathrm{1}=v_\mathrm{l}-v_\mathrm{c}.\]The boat must travel distance x with this speed. It will take time t1:
\[t_\mathrm{1}=\frac{x}{v_\mathrm{l}-v_\mathrm{c}}.\]Time t2 from Mr. Brown to Mr. Jones
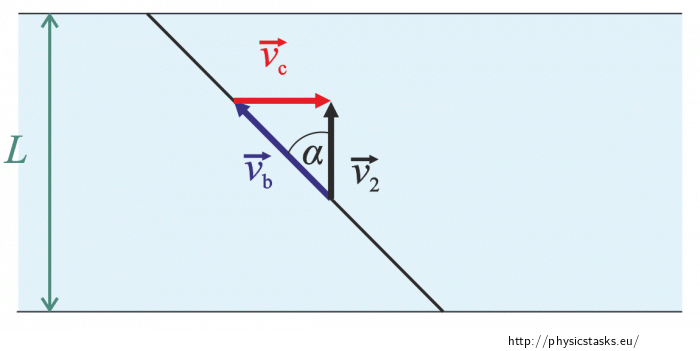
If Mr. Smith and Mr. Brown want to land at Mr. Jones's cottage, they cannot head straight to it (the current would carry them away). Instead, they need to sail in a manner depicted below:
Figure 2:
Net speed:
\[v_\mathrm{2}=\sqrt{v_\mathrm{b}^{2}-v_\mathrm{c}^{2}}.\]Time t2:
\[t_\mathrm{2}=\frac{L}{v_\mathrm{2}}=\frac{L}{\sqrt{v_\mathrm{b}^{2}-v_\mathrm{c}^{2}}}.\]We have determined time t1 it took Mr. Smith to sail to Mr. Brown and then time t2 it took them to sail to Mr. Jones.
We obtain the total duration of the journey t by adding both times:
\[ t=t_\mathrm{1}+t_\mathrm{2}=\frac{x}{v_\mathrm{b}-v_\mathrm{c}}+\frac{L}{\sqrt{v_\mathrm{b}^{2}-v_\mathrm{c}^{2}}}.\]Numerically:
\[t=\left(\frac{500}{2-1}+\frac{200}{\sqrt{3}}\right)\,\mathrm{s}=615\,\mathrm{s}.\]Answer
Mr. Smith and Mr. Brown will get to Mr. Jones in time t:
\[ t=\frac{x}{v_\mathrm{l}-v_\mathrm{r}}+\frac{L}{\sqrt{v_\mathrm{l}^{2}-v_\mathrm{r}^{2}}}.\]Numerically:
\[t=615\,\mathrm{s}.\]