A solid slides along the surface of a ball
Task number: 653
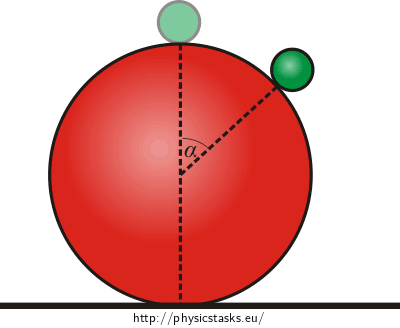
A small solid slides down from the highest point of a ball with a radius R along the surface of the ball without friction.
- A) In what height h after the highest point does the solid disconnect from the surface of the ball?
B) Work out the speed of the solid in the moment of the disconnection from the surface of the ball if it had a zero speed in the highest point.
C) In what distance from the point of contact of the ball with a horizontal table does the solid land on the table?
Hint 1A
Draw a picture of the forces affecting when the solid is on the top of the ball, and mark the place where you expect the disconnection of the solid from the surface of the ball.
Will it make our job easy if we distribute these forces appropriately?
Hint 2A
Write the motion equation for the solid and rewrite it into the scalar form.
Hint 3A
Express cosα by the radius of the ball and the sought height h.
Realise what equation holds for the normal acceleration of the solid.
Hint 4A
Due to the fact that the solid slides along the ball without friction, we can determine its speed in the moment of its disconnection under the law of conservation of mechanical energy.
Hint 5B
The magnitude of the speed of the solid in the moment of the disconnection is given by equation (5). Just substitute.
Find out what angle the velocity forms with the horizontal table.
Hint 6C
What kind of motion does the solid make after the disconnection from the ball? How does the distance change with the time in the horizontal and vertical direction?
Hint 7C
What height does the solid fall from? How long does the fall take? What distance does the solid cover in the horizontal direction?
Don’t forget to include in the final result the perpendicular distance of the place of the disconnection of the solid from the contact of the ball with the table.
COMPLETE SOLUTION
A. In what height after the highest point does the solid disconnect from the surface of the ball?
We draw a picture and mark the affecting forces:
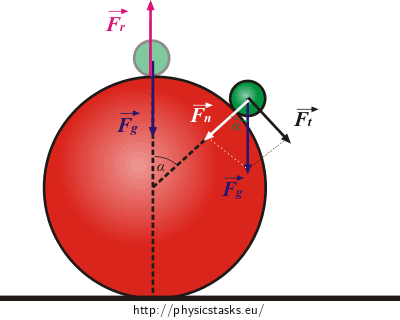
On the top of the ball:
\(\vec{F}_g\) ..... the weight
\(\vec{F}_r\) ..... force by which the ball affects the solid
in the place of disconnection from the ball:
\(\vec{F}_g\) ..... the weight
(In the moment of the disconnection the ball stops affecting the solid with a force and force \(\vec{F}_r\) equals zero.)
The force \(\vec{F}_g\) decomposes into two components:
Normal, oriented into the centre of the ball....\(\vec{F}_n\)
Tangential, oriented in the direction of the speed of the solid in the moment of the disconnection .... \(\vec{F}_t\)
We will proceed from the Newton`s second law in the form:
\[\vec{F}_{r} + \vec{F}_{g} = m\vec{a}\]The magnitude of the force F will be equalled zero in the moment of the disconnection of the solid from the surface of the ball, and thus the equation will have a simpler form:
\[\vec{F}_{g} = m\vec{a}\]We rewrite it to a scalar form:
in the tangential direction:
\[F_{g}\sin\alpha = ma_{t}\tag{1}\]in the normal direction:
\[F_{g}\cos\alpha = ma_{n}\tag{2}\]Where at is a tangential acceleration and an is a normal acceleration.
Express cosα by the radius of the ball and the sought height h.
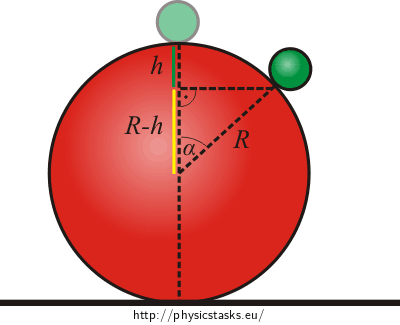
The picture implies that:
\[\cos\alpha = \frac{R-h}{R}\tag{3}\]The following holds for magnitude of centripetal (normal) acceleration by the circular motion with the radius R, then: \(a_{n} = \frac{v^2}{R}\)
Substitute into equation (2):
\[mg\frac{R-h}{R} = m\frac{v^2}{R}\]Where:
\[v^2 = g(R-h)\tag{4}\]Due to the fact that the solid slides along the ball without friction, we can determine its speed in the moment of its disconnection under the law of conservation of mechanical energy.
Choose a zero level of potential energy in the place of the disconnection, and therefore it is true that:
\[mgh = \frac{1}{2}mv^2\]Where:
\[v^2 = 2gh\tag{5}\]Substitute the equation (5) into equation (4):
\[2gh = g(R-h)\] \[3h = R\] \[h = \frac{R}{3}\]
B. What speed does the solid have in the moment of disconnection?
The magnitude of the speed of the solid is given by the equation (5). Just substitute. We determine what angle the speed forms with the horizontal direction.
Substitute this expression \(h = \frac{R}{3}\) into equation (5) :
\[v = \sqrt{\frac{2}{3}gR}\tag{6}\]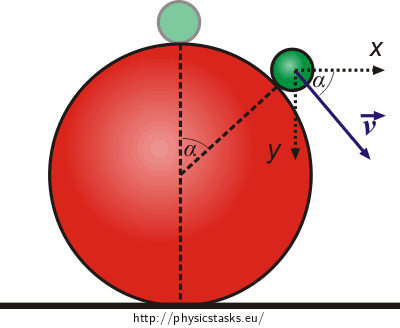
The picture implies that the velocity of the solid forms angle α with the horizontal table in the moment of the disconnection.
C. In what distance from the ball does the solid land?
At the start we realize what kind of motion the solid makes after the disconnection from the ball and how the distance changes with the time in the horizontal and vertical direction?
It is an inclined throw, in other words projectile motion. In the horizontal direction it performs a constant linear motion, in the vertical direction it is a case of a down inclined throw. The coordinates change with the time according to the following equations:
\[x = v_x t = vt\cos\alpha\] \[y = v_y t + \frac{1}{2}gt^2 = vt\sin\alpha + \frac{1}{2}gt^2\]According to the equation (3):
\[\cos\alpha = \frac{R-h}{R} = \frac{R-\frac{R}{3}}{R} = \frac{2}{3}\]By using the Pythagorean Theorem:
\[\sin\alpha = \frac{\sqrt{R^2 - (R-h)^2}}{R} = \frac{\sqrt{R^2 - \frac{4}{9}R^2}}{R} = \frac{\sqrt{5}}{3}\]We substitute:
\[x = \frac{2}{3}vt\tag{7}\] \[y = \frac{\sqrt{5}}{3}vt + \frac{1}{2}gt^2 \tag{8}\]The solid falls from the height \(\frac{5}{3}R\).
We find out the duration of the fall from equation (8) if we take into account what distance the solid has to cover during its fall to the table:
\[y = \frac{5}{3}R\] \[\frac{5}{3}R = \frac{\sqrt{5}}{3}vt + \frac{1}{2}gt^2 = \frac{\sqrt{5}}{3}\sqrt{\frac{2}{3}gR}t + \frac{1}{2}gt^2\]We adjust:
\[\frac{1}{2}gt^2 + \frac{1}{3}\sqrt{\frac{10}{3}gR}t - \frac{5}{3}R = 0\]Multiply by six:
\[3gt^2 + 2\sqrt{\frac{10}{3}gR}t - 10R = 0\]We express time by expression for the roots of the quadratic equation and we take into consideration only the positive root because negative time makes no physical sense.
\[D = \frac{40}{3}gR + 120gR = \frac{400}{3}gR\]And so:
\[t = \frac{-\sqrt{\frac{10}{3}gR} + 10\sqrt{\frac{1}{3}gR}}{3g}\]The solid covers the distance in the horizontal direction given by equation (7):
\[x = \frac{2}{3}vt = \frac{2}{3}\sqrt{\frac{2}{3}gR}(\frac{-\sqrt{\frac{10}{3}gR} + 10\sqrt{\frac{1}{3}gR}}{3g})\]Multiply and adjust:
\[x = (\frac{20}{27}\sqrt{2} - \frac{4}{27}\sqrt{5})R =\frac{4}{27}R (5\sqrt{2} - \sqrt{5})\]We have to add the horizontal distance which the solid covered along the surface of the ball to this distance.
\[d = R\sin\alpha = \frac{\sqrt{5}}{3}R\] The resultant distance is: \[L = x + d = \frac{4}{27}R (5\sqrt{2} - \sqrt{5}) + \frac{\sqrt{5}}{3}R = \frac{R}{3}(\frac{20\sqrt{2}}{9} -\frac{4\sqrt{5}}{9} + \sqrt{5})\] \[L = \frac{5R}{27}(4\sqrt{2} + \sqrt{5}) \dot= 1.46 R\]Answer
A) The solid is disconnected from the surface of the ball in the height equalling the third of the radius of the ball.
\[h = \frac{R}{3}\]B) The magnitude of the speed of the solid is in the moment of its disconnection:
\[v = \sqrt{\frac{2}{3}gR}\]Velocity of the solid forms an angle α with the horizontal direction in the moment of the disconnection.
C) The distance between the point (where the ball touches the table) and the point (where the solid lands) is:
\[L = \frac{5R}{27}(4\sqrt{2} + \sqrt{5}) \dot= 1.46 R\]




