A Cannon Firing Down a Hill
Task number: 1749
There is a cannon firing from the top of a hill that forms an angle of 30° with a horizontal plane. At the moment of the shot, the barrel of the cannon forms a certain elevation with the horizontal plane and it is aimed in such a way that the projectile lands on the bottom part of the hill 6 km from the cannon. Determine the minimum speed of the projectile at the moment it was fired from the barrel and the value of the elevation of the barrel. Neglect all resistive forces.
Notation
φ = 30° the angle between the slope of the hill and the horizontal plane d = 6 km distance from the cannon to where the projectile lands vmin = ? minimum speed of the projectile when leaving the barrel α0 = ? elevation angle of the barrel and the velocity vmin Method Description
Our goal is to find the initial speed as a function of the elevation α: v0 = v0(α). Using differential calculus we will then find such an elevation α0 at which this function (= initial speed) has a minimum. We will find the minimum speed by substituting the value of such α0 into v0 = v0(α)
Hint 1
Draw a picture of the situation (including the location of the landing) before you start solving this problem. Introduce an appropriate coordinate system and find the coordinates of the point of the landing using the given values. Pay close attention to this task, the picture will be the roots of a successful solution to this problem.
Hint 2
What kind of motion will the projectile perform? Write the equation of the time dependence of each component of the velocity vx(t), vy(t) and the time dependence of the coordinates of the projectile x(t), y(t).
Hint 3
You know the coordinates of the point of landing D, therefore you can calculate the duration of the flight of the projectile.
Hint 4
Our goal is to get to the equation v0 = v0(α). Substitute the duration of the flight calculated in equation (8) into the equation (7) and express the initial speed v0 as a function of elevation α.
Hint 5
How do we find the elevation at which equation (10) has a minimum? Would it help to differentiate the function? How? Do the calculations and find the elevation α0.
Hint 6
We found the elevation of the minimum speed, now we only need to calculate the speed vmin itself. What equation would be the most convenient to use?
Complete Solution
The situation and the coordinate system are shown in the picture below:
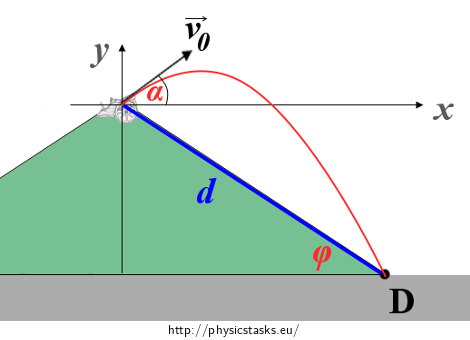
The trajectory of the projectile is in red. The origin of the coordinate system is positioned on the top of the hill, the letter D represents the location of the landing of the projectile. We can easily find the coordinates of the point D using trigonometry.
\[D\,=\,[x_D, y_D]\,=\,[d\cos{\varphi}, -d\sin{\varphi}]\tag{1}\]After leaving the barrel, the projectile is in a compound motion that we call an oblique throw (it’s a compound of free fall and two uniform linear motions, one in the direction of the x axis, the other in the direction of the y axis). For the components of the speed in the direction of the two axes during this motion with an initial speed v0 and an elevation α it holds that:
\[v_x(t)\,=\,v_0\cos{\alpha},\tag{2}\] \[v_y(t)\,=\,v_0\sin{\alpha}\,-\,gt,\tag{3}\]where g is the gravitational acceleration. We can get the time dependence of the coordinates of the projectile either from the formulas for the displacement of a uniform and uniformly accelerated linear motion, or by integrating equations (2) and (3). Either way we get:
\[x(t)\,=\,v_0t\cos{\alpha},\tag{4}\] \[y(t)\,=\,v_0t\sin{\alpha}\,-\,\frac{1}{2}gt^2.\tag{5}\]We have already expressed the coordinates of the point D earlier; by substituting them into equations (4) and (5) we get for the duration of the flight tD:
\[d\cos{\varphi}\,=\,v_0t_D\cos{\alpha},\tag{6}\] \[-d\sin{\varphi}\,=\,v_0t_D\sin{\alpha}\,-\,\frac{1}{2}gt_D^2.\tag{7}\]We can calculate the duration tD most easily from equation (6):
\[t_D\,=\,\frac{d\cos{\varphi}}{ v_0\cos{\alpha}}.\tag{8}\]We will substitute the flight duration tD calculated in equation (8) into equation (7) and express the dependence of the speed on elevation v0 = v0(α):
\[-d\sin{\varphi}\,=\,v_0(\frac{d\cos{\varphi}}{v_0\cos{\alpha}})\sin{\alpha}\,-\,\frac{1}{2}g(\frac{d\cos{\varphi}}{v_0\cos{\alpha}})^2.\tag{9}\]Solving for v0 we get:
\[-2dv_0^2\sin{\varphi}\cos^2{\alpha}\,=\,2dv_0^2\cos{\varphi}\cos{\alpha}\sin{\alpha}\,-\,gd^2\cos^2{\varphi},\] \[gd\cos^2{\varphi}\,=\,v_0^2(2\sin{\varphi}\cos^2{\alpha}\,+\,\sin{2\alpha}\cos{\varphi}),\] \[v_0\,=\, v_0(\alpha)\,=\,\sqrt{\frac{dg\cos^2{\varphi}}{2\sin{\varphi}\cos^2{\alpha}\,+\,\sin{2\alpha}\cos{\varphi}}}.\tag{10}\]We will differentiate equation (10) with respect to α and we will find such α0 at which the derivative equals zero. We know from differential calculus that that is where function (10) has an extremum – in this case a minimum. (We won’t prove that it really is a minimum here, but it can be done with a graph of the function or the second derivative).
Differentiating equation (10) we get:
\[\frac{dv_0}{d{\alpha}}\,=\,(\sqrt{dg\cos^2{\varphi}})(-\frac{1}{2})(2\cos^2{\alpha}\sin{\varphi}\,+\,\sin{2\alpha}\cos{\varphi})^{-\frac{3}{2}}{\cdot}\] \[{\cdot}(4\cos{\alpha}(-\sin{\alpha})\sin{\varphi}\,+\,2\cos{2\alpha}\cos{\varphi}),\tag{11}\] \[\frac{dv_0}{d{\alpha}}\,=\,-\frac{1}{2}\sqrt{\frac{dg\cos^2{\varphi}}{(2\cos^2{\alpha}\sin{\varphi}\,+\,\sin{2\alpha}\cos{\varphi})^3}}{\cdot}\] \[{\cdot}(-4\cos{\alpha}\sin{\alpha}\sin{\varphi}\,+\,2\cos{2\alpha}\cos{\varphi}).\tag{12}\]We are looking for such an elevation α0 at which the derivative is equal to zero, therefore it is evident that it isn’t necessary to consider the always-positive square root:
\[\frac{dv_0}{d{\alpha}}\,=\,0\,\Leftrightarrow\,2\cos{\alpha_0}\sin{\alpha_0}\sin{\varphi}\,=\,\cos{(2\alpha_0)}\cos{\varphi}.\tag{13}\]Using the double-angle formula we get:
\[\sin{2\alpha_0}\,=\,\cos{2\alpha_0}\frac{\cos{\varphi}}{\sin{\varphi}},\tag{14}\] \[\tan{2\alpha_0}\,=\,\cot{\varphi}.\tag{15}\]Numerically:
\[\tan{2\alpha_0}\,=\,\cot{30°}\,=\,\sqrt{3}\,\Rightarrow\,2\alpha_0\,=\,60°\,\Rightarrow\,\alpha_0\,=\,30°.\]The elevation that corresponds to the minimum initial speed is 30°.
We’ve got the dependence of the initial speed on elevation from equation (10), we can substitute the elevation α0 into it. Numerically:
\[v_{min}\,=\,v_0(\alpha_0)\,=\,\sqrt{\frac{6\,000{\cdot}10{\cdot}(\cos{30°})^2}{2\sin{30°}(\cos{30°})^2\,+\,\sin{60°}\cos{30°}}}\,\mathrm{m}\cdot\mathrm{s}^{-1},\] \[v_{min}\,=\,\sqrt{30000}\,\mathrm{m}\cdot\mathrm{s}^{-1}\,\dot=\,173\,\mathrm{m}\cdot\mathrm{s}^{-1}.\]The minimum initial speed of the projectile was approximately 173 m·s−1.
Answer
The minimum initial speed with which the projectile has to leave the barrel of the cannon is approximately 173 m·s−1, the elevation in this case is 30°.




