Little Paulie
Task number: 2227
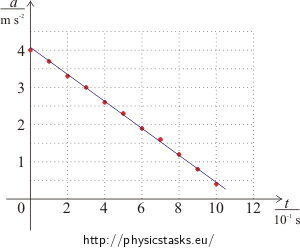
Little Paulie started off on a bike on a straight road. The acceleration dependence on time is given by the following table:
| t / 10-1s | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| a / m·s-2 | 4,0 | 3,7 | 3,3 | 3,0 | 2,6 | 2,3 | 1,9 | 1,6 | 1,2 | 0,8 | 0,4 |
Draw a graph and determine the shape of the function a(t). Determine the course of Paulie’s speed and position dependence on time from it.
Suppose that Paulie was not moving at time t = 0 s and was at the origin of the coordinate system.
Comment: We should speak about the absolute value of acceleration and the absolute value of speed to be more precise. The movement is one-directional and its direction is not changing, thus we will speak about acceleration and speed.
Hint 1: Graph of Paulie’s acceleration dependence on time
Draw a graph of acceleration dependence on time from the given table.
What is the graph of the given dependence?
Hint 2: Expressing the function a(t)
Use the slope-intercept form of a line to express the function a(t).
Hint 3: Paulie’s speed time dependence
You know how Paulie’s speed changes with time. How to you find out his speed dependence on time?
Hint 4: Paulie’s position course
You already know the time dependence of Paulie’s speed.
How do you find his position dependence on time?
Solution
Comment: Equations should be written for example as:
\[y\,=\,1\,\mathrm{m}-2\,\mathrm{m \cdot s^{-1}}\cdot t\,.\]We don’t write units for simplification.
We will draw a graph of Paulie’s acceleration dependence on time according to the table:
The graph is a line.
We will use the slope-intercept form of a line to express the function a(t):
\[a\left(t\right)\,=\,-kt+q\,,\]\(q\, =\, 4\) (intersection with the vertical axis)
\(k\,=\,tg\,\alpha\) (slope)
\[tg\alpha\,=\,\frac{\Delta{a}}{\Delta{t}} \,=\, \frac{4-0{,}4}{1} \,=\, 3{,}6\,.\]( α is the angle that the line clamps with the x-axis)
Therefore: \[a\left(t\right)\,=\,-3{,}6t+4\,.\]The course of Paulie’s speed can be found by integration of a(t):
\[v\left(t\right)\,=\,\int{a\left(t\right)}dt\,=\,\int{\left(-3{,}6t+4\right)}dt\,,\] \[v\left(t\right)\,=\,-\frac{3{,}6}{2}t^{2}+4t+C\,=\,-1{,}8^{2}+4t+C\,.\]We can find the constant C from the initial conditions:
for t = 0 s is v = 0 m s-1,
thus C = 0.
We get:
\[v\left(t\right)\,=\,-1{,}8t^{2}+4t\,.\]The course of Pavlík’s speed can be found by integration of v(t):
\[s\left(t\right)\,=\,\int{v\left(t\right)}dt\,=\,\int{\left(-1{,}8t^{2}+4t\right)}dt\,=\, -\frac{1{,}8}{3}t^{3}+\frac{4}{2}t^{2}+D\,,\] \[s(t)\,=\, -0{,}6t^{3}+2t^{2}+D\,.\]We can find the constant D from the starting conditions:
for t = 0 s is s = 0 m,
thus D = 0.
Therefore: \[s\left(t\right)\,=\,-0{,}6t^{3}+2t^{2}\,.\]Answer
The graph of Paulie’s acceleration dependence on time:
The function a(t) is expressed as:
\[a\left(t\right)\,=\,-3{,}6t+4\,.\]The course of speed v(t) is:
\[v\left(t\right)\,=\,-1{,}8t^{2}+4t\,.\]The course of position s(t) is:
\[s\left(t\right)\,=\,-0{,}6t^{3}+2t^{2}\,.\]
