A Rocking Semi-Cylinder
Task number: 1755
There is a homogeneous semi-cylinder of radius r and mass m lying on a horizontal plane.
a) Determine the moment of inertia of the semi-cylinder about the line where the semi-cylinder touches the plane.
b) We will displace the semi-cylinder by a small angle from its equilibrium position and let it rock. What will be the period of the rocking?
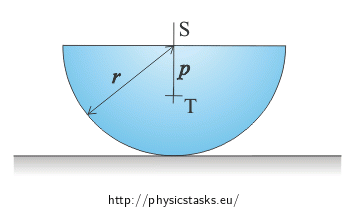
Let us assume that the friction between the semi-cylinder and the plane is sufficient/big enough that the semi-cylinder rolls without slipping and that the rolling resistance is negligible.
The distance between the center of gravity of the semi-cylinder and the point S is \(p=\frac{4r}{3\pi}\)
When working with small angles we can approximate that \(\sin\alpha\dot{=}\alpha\,,\) \(\cos\alpha=1-2sin^2\frac{\alpha}{2}\dot{=}1-\frac{\alpha^2}{2}\,.\)
Hint for a) 1
Use Steiner’s theorem and the moment of inertia about the axis that passes through the centers of the bases of a full cylinder to calculate the required moment of inerta.
Hint for b) 1
Let us assume that the rocking of the semi-cylinder is not being damped by resistive forces and that the semi-cylinder performs a harmonic motion.
The formulas for the instantaneous angular displacement from the equilibrium position of the semi-cylinder and for the instantaneous angular speed are similar to the ones that apply for a ball oscillating on a spring. Write them down.
Hint for b) 2
Use the law of conservation of energy to further solve the problem. Write down what the mechanical energy of the semi-cylinder is when we displace it from its equilibrium position and what its energy is when passing through the equilibrium position. Don’t forget to choose the zero level of potential energy.
Complete Solution
a)Steiner’s theorem says that if we know the moment of inertia JT about an axis passing through the center of gravity of a body of mass m, we can express the moment of inertia about a parallel axis at a distance d as:
\[J=J_T+md^2\,.\]The moment of inertia of a cylinder about an axis that passes through the center of the bases is:
\[J=\frac{1}{2}mr^2\,.\]If we added another semi-cylinder to our semi-cylinder, we would get a full cylinder with the moment of inertia about the rotational symmetry axis of \(\frac{1}{2}2mr^2\).
Our semi-cylinder only has half the mass of the full cylinder, but the mass is distributed in the same ratio relative to said axis, therefore:
\[J_S=\frac{1}{2}mr^2\,.\]According to Steiner’s theorem:
\[J_S=J_T+mp^2\,.\]Let us denote the required moment of inertia by JH. According to Steiner’s Theorem it holds that:
\[J_H=J_T+m(r-p)^2\,.\]We will substitute for JT, JS and p:
\[J_H = J_S - mp^2 + mr^2 - 2mrp + mp^2\,,\] \[J_H = J_S+ mr^2-2mrp=\frac{1}{2}mr^2+mr^2-2mr\frac{4r}{3\pi}\,,\] \[J_H=mr^2(\frac{3}{2}-\frac{8}{3\pi})\,.\tag{1}\] b)Let us assume that the rocking of the semi-cylinder is not being damped by resistive forces and that the semi-cylinder performs a harmonic motion.
For the instantaneous angular displacement α it holds that:
\[\alpha (t)=\alpha_0\cos\omega t\,,\]where \(\omega=2\pi f = \frac{2\pi}{T}.\)
We get the instantaneous angular speed ω by differentiating with respect to t:
\[\omega (t) = - \alpha_0\omega\sin\omega t\,.\] Let us denote: \[\omega_m=\omega\alpha_0\,.\tag{2}\]We use the law of conservation of energy to further solve the problem. We write down what the mechanical energy of the semi-cylinder is when we displace it from its equilibrium position and what its energy is when passing through the equilibrium position. We choose the zero level of potential energy to be in the center of gravity of the semi-cylinder.
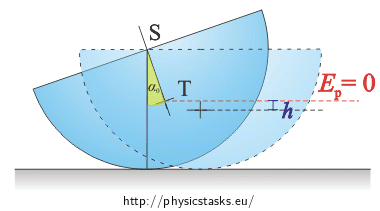
When we displace the semi-cylinder we raise the center of gravity by a height h, which is the difference of distances of points S and T - that is the distance p - and the orthogonal projection of this distance after displacing the semi-cylinder, pcosα0:
\[h=p-p\cos\alpha_0\dot{=}p(1-(1-\frac{\alpha^2}{2}))=\frac{2r\alpha^2}{3\pi}\,.\tag{3}\]At the moment of the displacement the kinetic energy of the semi-cylinder is zero and its potential energy is:
\[E_{p1}=mgh=\frac{2mgr\alpha^2}{3\pi}\,.\]When passing through the equilibrium position the potential energy of the semi-cylinder is zero and the kinetic energy is:
\[E_{k2} = \frac{1}{2}J\omega_m^2\,.\]According to the law of conservation of energy it holds that:
\[E_{k2} = E_{p1}\,, \] \[\frac{1}{2}J_H\omega_m^2=mgh\,.\]We substitute for \(J_H, \omega_m, h\) from equations (1), (2), (3):
\[\frac{1}{2}mr^2(\frac{3}{2}-\frac{8}{3\pi})(\omega\alpha_0)^2 = mg\frac{2r\alpha_0^2}{3\pi}\,.\]We solve for ω:
\[\frac{1}{2}r(\frac{3}{2}-\frac{8}{3\pi})\omega^2=g\frac{2}{3\pi}\,,\] \[\omega^2=\frac{4g}{3\pi r(\frac{3}{2}-\frac{8}{3\pi})}\,,\] \[\omega^2=\frac{8g}{ r(9\pi-16)}\,.\]And since: \(\omega=\frac{2\pi}{T}\):
\[T=2\pi\sqrt{\frac{r(9\pi-16)}{8g}}\,,\] \[T=\pi\sqrt{\frac{r(9\pi-16)}{2g}}\,.\]Answer
a) The required moment of inertia is:
\[J_H=mr^2(\frac{3}{2}-\frac{8}{3\pi})\,.\]b) The semi-cylinder oscillates with the period:
\[T=\pi\sqrt{\frac{r(9\pi-16)}{2g}}\,.\]


