The Cyclist Riding Along the Road
Task number: 378
A cyclist is going in a straight line at a uniform velocity 27 km\(\cdot\)h-1. The resistance force can be expressed as Fres = kv2, where k = 0.3 assuming the unit of velocity is metres per second and the unit of force is newtons. The mass of the cyclist together with the bicycle is 70 kg. Neglect the rolling-resistance force.
a) With what force does the road push the bicycle to keep the motion uniform?
b) What work has to be done by the cyclist over a distance of 1200 m? What is the power of the cyclist during the ride?
c) What is the highest velocity the cyclist could achieve with a fixed power of 600 W?
Hint a) - the road exert a force
Draw a free body diagram of a riding cyclist.
What can one say about the net force exerted on the bicycle when the cyclist is moving with constant speed?
Hint b1) - the work done by the cyclist
Neglecting losses of mechanical energy the work done by the cyclist is equal to the work done by the force with which the road pushes the bicycle.
Hint b2) - the power of the cyclist
What is the power of the cyclist providing that we know the force and the velocity of the cyclist.
Hint c) - maximum velocity at given power
The power is now given. Find the maximum velocity.
Do not forget the force of the road pushing the bicycle equals the resistant force. So, it could be expressed as:
\[F=kv^{2}\tag{2}\]Numeric calculation
a)
Given:
\[k=0.3\,\mathrm{kgm^{-1}}\] \[v=27\,\mathrm{kmh^{-1}}=7.5\,\mathrm{m s^{-1}}\]Desired: \[F=?\]
\[F=kv^{2}\] \[F=0.3{\cdot}7.5^{2}\,\mathrm{N}\] \[F=16.9\, \mathrm{N}\]b)
Given:
\[F=16.9\, \mathrm{N}\] \[s=1200\, \mathrm{m}\] \[v=7.5\, \mathrm{m s^{-1}}\]Desired: \(W=?\), \(P=?\)
\[W=Fs\] \[W=16.9{\cdot}1200\,\mathrm{J}\] \[W=20280\, \mathrm{J}\,\dot=20.3\ \mathrm{kJ}\] \[P=Fv\] \[P=16.9{\cdot}7.5\,\mathrm{W}\] \[P=127\, \mathrm{W}\]c)
Given:
\[P=600\, \mathrm{W}\] \[k=0.3\,\mathrm{kgm^{-1}}\]Desired: \(v=?\)
\[v=\sqrt[3]{\frac{P}{k}}\] \[v=\sqrt[3]{\frac{600}{0.3}}\,\mathrm{m s^{-1}}\] \[v=12.6\, \mathrm{m s^{-1}}=45.4\, \mathrm{kmh^{-1}}\]Answer
a)
The road pushes the bicycle by the force \(F=kv^2=16.9\,\mathrm{N}\).
b)
Cyclist has to do the work \(W=Fs\,\dot=20.3\ \mathrm{kJ}\). The power during the ride is \(P=Fv=127\,\mathrm{W}\).
c)
Cyclist could ride at the maximum velocity of \(v=\sqrt[3]{\frac{P}{k}}=45.4\, \mathrm{kmh^{-1}}\) while the power is 600 W.
Notice: What would change if ...
Let’s try count what would change if the velocity of the cyclist was 18 km\(\cdot\)h-1 or 45 km\(\cdot\)h-1.
For the velocity 18 km\(\cdot\)h-1:
a)
\[k=0.3\,\mathrm{kgm^{-1}}\] \[v=18\,\mathrm{kmh^{-1}}=5\,\mathrm{m s^{-1}}\] \[F=?\] \[F=kv^2\] \[F=0.3{\cdot} 5^2\,\mathrm{N}\] \[F=7.5 \,\mathrm{N}\]b)
\[F=7.5\,\mathrm{N}\] \[s=1200\,\mathrm{m}\] \[v=5\mathrm{m s^{-1}}\] \[W=Fs\] \[W=7.5 {\cdot} 1200\,\mathrm{J}\] \[W=9000\, \mathrm{J}=9\, \mathrm{kJ}\] \[P=Fv\] \[P=7.5{\cdot} 5\,\mathrm{W}\] \[P=37.5\, \mathrm{W}\]c)
\[P=600\,\mathrm{W}\] \[k=0.3\] \[v=\sqrt[3]{\frac{P}{k}}\] \[v=\sqrt[3]{\frac {600}{0.3}}\,\mathrm{m s^{-1}}\] \[v=12.5\,\mathrm{m s^{-1}}\]The smaller the velocity, the smaller the resistance force and also the smaller the force of the road pushing on the bicycle. Both the work done by the cyclist and his or her power are smaller. The outcome of variation c) is similar.
For the cyclist’s velocity 45 km\(\cdot\)-1:
a)
\[k=0.3\,\mathrm{kgm^{-1}}\] \[v=45\mathrm{kmh^{-1}}=12.5\mathrm{m s^{-1}}\] \[F=?\] \[F=kv^2\] \[F=0.3{\cdot} 12.5^2\,\mathrm{N}\] \[F=46.9 \,\mathrm{N}\]b)
\[F=46.9\,\mathrm{N}\] \[s=1200\,\mathrm{m}\] \[v=12.5\mathrm{m s^{-1}}\] \[W=Fs\] \[W=46.9 {\cdot} 1200\,\mathrm{J}\] \[W=56280\, \mathrm{J}\,\dot=56.3\ \mathrm{kJ}\] \[P=Fv\] \[P=46.9{\cdot} 12.5\,\mathrm{W}\] \[P=586\, \mathrm{W}\]c)
\[P=600\,\mathrm{W}\] \[k=0{,}3\] \[v=\sqrt[3]{\frac{P}{k}}\] \[v=\sqrt[3]{\frac {600}{0.3}}\,\mathrm{m s^{-1}}\] \[v=12.5\,\mathrm{m s^{-1}}\]The bigger the velocity, the bigger both the resistance force and the force of the road pushing the bicycle. Both the work done by the cyclist and his or her power are larger. The outcome of variation c) is similar.
Complete solution of point a)
Assuming the cyclist together with the bycicle is one object we will mark all exerting forces.
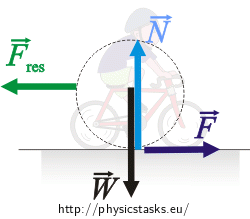
\(\vec{F}\) ... the desired force with which the road pushes the bicycle
\(\vec{N}\) ... the normal force of the road acting on the bicycle
\(\vec{W}\) ... the weight
\(\vec{F}_{res}\) ... the resistance force
The net force acting on the cyclist together with the bicycle during uniform rectilinear motion has to equal zero because the acceleration is zero.
\[\vec{W}+\vec{N}+\vec{F}_{res}+\vec{F}=0\]The weight \(\vec{W}\) acting on the cyclist-bicycle system is the same magnitude as the normal force \(\vec{N}\) of the road acting on the bicycle. It results from the Newton’s third law (law of reciprocal actions).
\[W-N=0\]The force \(\vec{F}\) exerted on the bicycle by the road has to be the same magnitude as the resistance force \(\vec{F}_{res}\).
\[F=F_{res}=kv^{2}\] \[F=0.3{\cdot}7.5^{2}\,\mathrm{N}\] \[F=16.9\, \mathrm{N}\]k ... the constant
v ... the velocity of the cyclist
Answer: The road pushes the bicycle by the force \(F=16.9\,\mathrm{N}\).
.Complete solution of point b)
The force pushing the bicycle is invariant in time and acts facing in direction of the movement. We can express the work done by this force as:
\[W=Fs=kv^2s\] \[W=16.9{\cdot}1200\,\mathrm{J}\] \[W=20280\, \mathrm{J}\,\dot=20.3\ \mathrm{kJ}\]W ... the work
F ... the desired force exerted on the bicycle by the road
s ... the moved distance
v ... the velocity of the cyclist
The instantaneous power could be expressed as:
\[P=\frac{dW}{dt}=\frac {dF\cdot s}{dt}=F\cdot\frac {ds}{dt}=F\cdot v\] \[P=Fv\] \[P=16.9{\cdot}7.5\,\mathrm{W}\] \[P=127\, \mathrm{W}\]Answer:
Cyclist has to do work \(W=20.3\ \mathrm{kJ}\). The power exerted during the ride is \(P=127\,\mathrm{W}\).
Complete solution of point c)
Insert the force F into expression \(P=Fv\).
\[F=kv^{2}\] \[P=kv^{3}\]Express the velocity:
\[v^{3}=\frac{P}{k}\]Extract this equation:
\[v=\sqrt[3]{\frac{P}{k}}\] \[v=\sqrt[3]{\frac{600}{0.3}}\,\mathrm{m s^{-1}}\] \[v=12.6\,\mathrm{m s^{-1}}=45.4\, \mathrm{km h^{-1}}\]Answer: Cyclist could ride at a maximum velocity of \(45.4\, \mathrm{kmh^{-1}}\) while the power is 600 W.




