Four Cubes with Three Springs
Task number: 2001
Four identical wooden cubes of mass m are connected together in a row with three identical springs of stiffness k. We push perpendicularly on the wall of the cube at the edge by a force \(\vec{F}\), so we make the cubes move with a uniformly accelerated motion with the acceleration of the magnitude a. Determine the magnitude of the force F and the compression of each spring if the coefficient of sliding friction between the cubes and the ground is f. Ignore the mass of the springs.

Notation
m1 mass of the first cube m2 mass of the second cube m3 mass of the third cube m4 mass of the fourth cube k stiffness of the springs f coefficient of sliding friction between any of the cubes and the ground a acceleration of the cubes \(\Delta l_1\) = ? compression of the first spring \(\Delta l_2\) = ? compression of the second spring \(\Delta l_3\) = ? compression of the third spring F = ? the magnitude of the exerting force Hint 1 - forces acting on the cubes
Think of the forces acting on each of the cubes and draw a picture.
Hint 2 - equations of motion
Write the equation of motion for each cube. Then choose a coordinate system and rewrite the equations into scalar forms.
Hint 3 - friction force and calculation of the force F
Realise what the magnitude of friction force between the cube and the ground is dependent on and how it can be expressed. Then calculate the force F from equations (6) - (9).
Hint 4 - forces compressing the springs (compression of the springs)
Express the magnitude of forces F1, F2, F3, compressing each of the springs from equations (7) - (9).
Hint 5 - calculation of the compression of springs
The compression of the springs is proportional to the magnitude of the forces compressing them. Write this relation into equations and calculate the compression of each of the springs.
Complete solution
The forces acting on the cubes:
We mark the forces acting on the cubes in the picture and then write the equations of motions for the cubes.
The forces acting on each of the cubes m1, m2, m3 and m4:
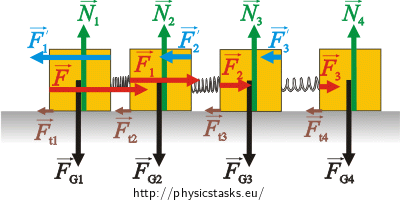
\[\vec{F}_{G_1}=\vec{F}_{G_2}=\vec{F}_{G_3}=\vec{F}_{G_4}=\vec{F}_{G} \] …the force of gravity acting on the each cube - m1, m2, m3 and m4 (the force of gravity is the same for each cube)
\[\vec{N}_{1}=\vec{N}_{2}=\vec{N}_{3}=\vec{N}_{4}=\vec{N}\] …the normal force which the ground exerts on the cubes m1, m2, m3 and m4 (this force is also the same for each cube)
\[\vec{F}_{t_1}=\vec{F}_{t_2}=\vec{F}_{t_3}=\vec{F}_{t_4}=\vec{F}_t\] …the friction force between the ground and each of the cubes m1, m2, m3 and m4 (the friction force is the same for each cube)
There are also these forces acting on the cubes:
Cube m1:
\(\vec{F}\)…the force by which we push the cube,
\(\vec{F}_1\prime\)…the force by which the second cube is acting on the first one.
Cube m2:
\(\vec{F}_1\)…the force by which the first cube is acting on the second one,
\(\vec{F}_2\prime\)…the force by which the third cube is acting on the second one.
Cube m3:
\(\vec{F}_2\)…the force by which the second cube is acting on the third one,
\(\vec{F}_3\prime\)…the force by which the fourth cube is acting on the third one.
Cube m4:
\(\vec{F}_3\)…the force by which the third cube is acting on the fourth one.
The equations of motion for the cubes are:
\[m_1:\qquad\vec{F}+\vec{N}+\vec{F}_{G}+\vec{F}_{t}+\vec{F}_{1}\prime\,=\,m\vec{a},\] \[m_2:\qquad\vec{F}_1+\vec{N}+\vec{F}_{G}+\vec{F}_{t}+\vec{F}_{2}\prime\,=\,m\vec{a},\] \[m_3:\qquad\vec{F}_2+\vec{N}+\vec{F}_{G}+\vec{F}_{t}+\vec{F}_{3}\prime\,=\,m\vec{a},\] \[m_4:\qquad\vec{F}_3+\vec{N}+\vec{F}_{G}+\vec{F}_{t}\,=\,m\vec{a}.\]Every cube is moving with the same acceleration.
To write the scalar equations of motion, we choose a coordinate system of the x,y axes so that the x axis is in the direction of the motion of the cubes. The y axis is perpendicular to the x axis.
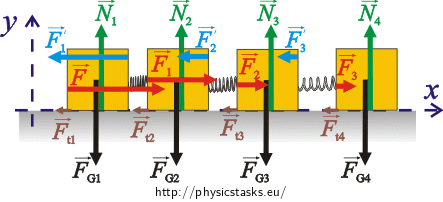
The scalar equations of motion for the cubes:
\[m_{1_x}:\qquad F-F_t-F_1\prime=ma,\tag{1}\] \[m_{2_x}:\qquad F_1-F_t-F_2\prime=ma,\tag{2}\] \[m_{3_x}:\qquad F_2-F_t-F_3\prime=ma,\tag{3}\] \[m_{4_x}:\qquad F_3-F_t=ma.\tag{4}\]The equations of motion in the direction of the y axis are the same for each cube:
\[m_y:\qquad N-F_G=0.\tag{5}\]The cube m1 acts via the first spring on the cube m2, and vice versa, the cube m2 acts via the same spring on the cube m1. Similarly with the pairs of cubes m2, m3 a m3, m4. According to the Newton’s third law of motion it holds for the magnitudes of forces that:
\[|\vec{F}_1| \,=\, |\vec{F}_1\prime|,\] \[|\vec{F}_2| \,=\, |\vec{F}_2\prime|,\] \[|\vec{F}_3| \,=\, |\vec{F}_3\prime|.\]We rewrite equations (1) - (4):
\[m_{1_x}:\qquad F-F_t-F_1=ma,\tag{6}\] \[m_{2_x}:\qquad F_1-F_t-F_2=ma,\tag{7}\] \[m_{3_x}:\qquad F_2-F_t-F_3=ma,\tag{8}\] \[m_{4_x}:\qquad F_3-F_t=ma.\tag{9}\]Expressing the friction force:
The friction force exerting on the cube is proportional to the pressure force of each of the springs exerting on the ground. The magnitude of this pressure force is, according to the Newton’s third law of motion, the same as magnitude of the force with which the ground pushes on the cube. Therefore the equation is:
\[F_t\,=\,fN.\]Force N can be expressed from the equation (5):
\[N\,=\,F_G.\]It holds for the friction force that:
\[F_t\,=\,fF_G=mgf.\tag{10}\]We add equations (6) - (9) together and express the forceF:
\[F-4F_t\,=\,4ma,\] \[F\,=\,4ma+4F_t.\]We substitute for the friction force from equation (10):
\[F\,=\,4ma+4mgf\,=\,4m\left(a+gf\right).\tag{11}\]Expressing the forces acting on the springs:
The force acting on the first spring can be calculated by adding equations (7), (8) and (9) together:
\[F_1-3F_t\,=\,3ma,\] \[F_1\,=\,3ma+3mgf\,=\,3m\left(a+gf\right).\tag{12}\]The force on the second spring can be calculated by adding equations (8) and (9) together:
\[F_2-2F_t\,=\,2ma,\] \[F_2\,=\,2ma+2mgf\,=\,2m\left(a+gf\right).\tag{13}\]The force on the third spring can be expressed from equation (9):
\[F_3\,=\,ma+mgf\,=\,m\left(a+gf\right).\tag{14}\]The compression of the springs:
The force compressing the spring is proportional to its compression Δl and also to the stiffness of the spring k. The equation for the force compressing the spring is:
\[F\,=\,k\Delta l.\]We express the compression:
\[\Delta l\,=\,\frac{F}{k}.\]The calculation of the compression for each of the springs:
\[\Delta l_1\,=\,\frac{F_1}{k}\,=\,\frac{3m\left(a+gf\right)}{k},\tag{15}\] \[\Delta l_2\,=\,\frac{F_2}{k}\,=\,\frac{2m\left(a+gf\right)}{k},\tag{16}\] \[\Delta l_3\,=\,\frac{F_3}{k}\,=\,\frac{m\left(a+gf\right)}{k}.\tag{17}\]Answer
The magnitude of force F is \[F\,=\,4m\left(a+gf\right).\]
The contraction of the first spring is: \[\Delta l_1\,=\,\frac{F_1}{k}\,=\,\frac{3m\left(a+gf\right)}{k}.\]
The contraction of the second spring is: \[\Delta l_2\,=\,\frac{F_2}{k}\,=\,\frac{2m\left(a+gf\right)}{k}.\]
The contraction of the third spring is: \[\Delta l_3\,=\,\frac{F_3}{k}\,=\,\frac{m\left(a+gf\right)}{k}.\]