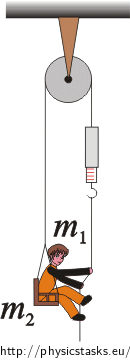
Boy on a pulley
Task number: 278
A metal seat with mass m2 = 32 kg hangs from one end of a rope that passes over a frictionless pulley attached to the ceiling. A spring scale hangs from the other end of the rope. A boy with mass m1 = 64 kg sitting on the hung seat is pulling the spring scale which shows the force of 600 N.
a) Find the acceleration of the boy and seat. Does the acceleration point downwards or upwards under given conditions.
b) Find the force that the boy exerts on the seat.
Consider both the pulley and the rope to be massless.
Hint 1 – the equations of motion (determining the acceleration)
Consider all forces acting on the boy and the seat. Draw a figure (a free body diagram) with all forces. Write down the equations of motion for the boy and the seat.
Recommendation: For clarity draw two figures, one for the boy and one for the seat.
Hint 2 – the scalar equations of motion, relations between the normal and tension forces
Choose a suitable frame of reference and write the equations of motion in a scalar form. Think of a relation between the normal force exerted on the boy by the seat and the normal force exerted on the seat by the boy. Consider also a similar relation between the tension forces.
Hint 3 – calculation of the acceleration
Add up the equations (5) and (6) and find the acceleration.
Hint 4 – the magnitude of the normal force
The magnitude of the normal force exerted on the seat by the boy can be expressed from the equation (6) by substituting the acceleration given by (7).
Complete solution
First we draw a figure (a free body diagram) with all forces acting on the boy and on the seat and write down the equations of motion for them.
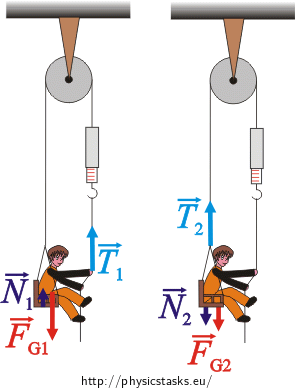
The forces acting on the boy:
\(\vec{N}_1\)...the normal force exerted on the boy by the seat
\(\vec{T}_1\)...the tension force by which the rope pulls on the boy
\(\vec{F}_{G_1}\)...the weight of the boy
The forces acting on the seat:
\(\vec{N}_2\)...the normal force exerted on the seat by the boy
\(\vec{T}_2\)...the tension force by which the rope pulls on the seat
\(\vec{F}_{G_2}\)...the weight of the seat
The equation of motion for the boy:
\[\vec{T}_1+\vec{N}_1+\vec{F}_{G_1}= m_1\vec{a}\tag{1}\]
The equation of motion for the seat:
\[\vec{T}_2+\vec{N}_2+\vec{F}_{G_2}= m_2\vec{a}\tag{2}\]
To write the equations of motion in a scalar form we choose a suitable frame of reference. We choose the axis y to point upwards in the direction of the tension forces.
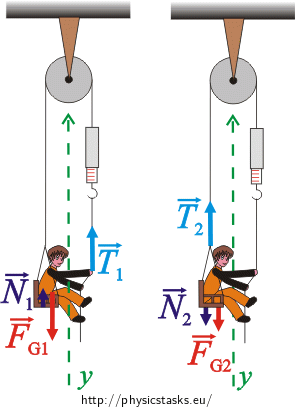
The scalar equation of motion for the boy:
\[T_1+N_1-F_{G_1}= m_1a\tag{3}\]
The scalar equation of motion for the seat:
\[T_2-N_2-F_{G_2}= m_2a\tag{4}\]
Since we consider the pulley to be massless it has no moment of inertia and thus has no effect on the tension of the rope. According to Newton’s third law the magnitudes of the tension forces are equal:
\[|\vec{T}_1|=|\vec{T}_2|\]
Once again according to Newton’s third law the normal force exerted on the seat by the boy is of the same magnitude as the force exerted on the boy by the seat:
\[|\vec{N}_1|=|\vec{N}_2|\]
Using these relations we can rewrite the equations (3) and (4) as:
\[T_2+N_2-F_{G_1}= m_1a\tag{5}\]
\[T_2-N_2-F_{G_2}= m_2a\tag{6}\]
Calculation of the acceleration a.
We add up the equations (5) and (6):
\[2T_2-F_{G_2}-F_{G_1}=(m_2+m_1)a\]
and express the acceleration as:
\[a=\frac{2T_2-F_{G_2}-F_{G_1}}{m_2+m_1}=\]
\[a=\frac{2T_2-m_2g-m_1g}{m_2+m_1}\]
\[a=\frac{2T_2}{m_2+m_1}-\frac{m_2g+m_1g}{m_2+m_1}= \frac{2T_2}{m_2+m_1}-g\tag{7}\]
For the given numerical values we get:
\[a=(\frac{2{\cdot}600}{32+64}-9.81)\,{m\cdot s^{-2}} =(\frac{1200}{96}-9.81)\,{m\cdot s^{-2}}\]
\[a =(12.5-9.81)\,{m\cdot s^{-2}}=2.69\,{m\cdot s^{-2}}\]
Note: The resulting acceleration is positive. Therefore, the boy and the seat are moving upwards in the direction of the y-axis. If we have chosen the y-axis to point downwards the acceleration would be negative.
Calculation of the magnitude of the normal force N2.
We express N2 from the equation (6):
\[N_2=T_2-F_{G_2}-m_2a\]
\[N_2=T_2-m_2g-m_2a\]
and substitute the acceleration given by the equation (7):
\[N_2=T_2-m_2g-m_2(\frac{2T_2}{m_2+m_1}-g)\]
\[N_2=T_2-\frac{2T_2m_2}{m_2+m_1}\]
\[N_2=\frac{T_2m_1+T_2m_2-2T_2m_2}{m_2+m_1}\]
\[N_2=T_2(\frac{m_1-m_2}{m_2+m_1})\tag{8}\]
For the given numerical values we get:
\[N_2=600(\frac{64-32}{32+64})\,\textrm{N}=\frac{600 \cdot (32)}{96}\,\textrm{N}=\frac{600}{3}\,\textrm{N}=200\,\textrm{N}\]
Complete answer
The acceleration of the boy and the seat is \[a = \frac{2T_2}{m_2+m_1}-g = 2.69\,{m\cdot s^{-2}}\] .
The acceleration points upwards under given conditions.
The magnitude of the force exerted on the seat by the boy is \[N_2 = T_2(\frac{m_1-m_2}{m_2+m_1})=200\,{N}\] .





