A Bullet and a Rod I
Task number: 4319
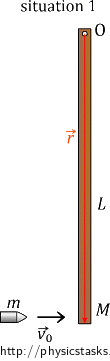
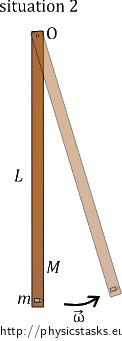
A bullet of a mass \(m\) travelling horizontally with a velocity \(\vec{v_{0}}\) hits the end of a wooden rod of a length \(L\) and a mass \(M\) and gets stuck in it. The rod is free to rotate around a horizontal axis passing through the upper end of the rod.
a) Determine the moment of inertia of the rod with respect to the horizontal axis of rotation.
b) Calculate the angular velocity with which the rod starts to rotate.
c) Calculate the ratio of the change in internal energy of the system of the bullet and the rod \(\Delta U\) to the initial kinetic energy of this system \(E_{k_{0}}\).
Analysis
Let us assume that the bullet penetrates the rod very quickly, stops inside it, and causes the rod to rotate with the angular velocity we aim to determine.
We will use the law of conservation of angular momentum to solve the task. We will focus on two situations; the first is just before the moment when the bullet hits the rod, and the second is the moment just after the hit. We will write down the total angular momentum of the system of the bullet and the rod in both of these situations and we will express the angular velocity we aim to determine from the equality of the moduli of the angular momenta.
When the bullet penetrates the rod, both the bullet and the rod heat up and deform, the mechanical energy is thus not conserved. We will calculate the change in internal energy from the difference of the total mechanical energy of the system of the bullet and the rod before the hit and after it.
Hint for a)
Suppose that the rod is homogeneous and thin. Revise the definition of the moment of inertia and how you understand it. Imagine the rod being divided into small segments (according to length or mass) and write down the moment of inertia for one such segment of the rod.
Hint for b)
Let us assume that the bullet penetrates the rod very quickly, stops in it, then the bullet and the rod start moving together. To solve question b), we use one of the laws of conservation. Consider which physical quantity is conserved in this situation.
Hint for c)
Write down the expression of mechanical energy of the system of the bullet and the rod before the bullet hits the rod and just after the hit. Think about the magnitudes of the energies; are they the same or not? How do you express the change in the internal energy of the system?
Solution of a)
We imagine a homogeneous and thin rod of a length L and a mass M to be divided into small segments, each of which has a length \(\Delta\)l and a mass \(\Delta\)M.

It holds for the moment of inertia of one such segment \(\Delta I_{rod}\):
\[ \Delta I_{rod} = \Delta M l^2. \tag{1}\]
We assume the rod to be homogeneous and thin; therefore, we can express the mass of one segment \(\Delta\)M using its linear density \(\lambda = \frac{M}{L} \) and the length \(\Delta\)l:
\[ \Delta M = \frac{M}{L} \Delta l . \tag{2}\]
We substitute equation (2) into equation (1). To get the total moment of inertia, we imagine dividing the rod into infinitely small segments and sum up their moments of inertia; in other words, we apply the integral.
\[ I_{rod}= \int_0^{L}{\frac{M}{L}l^2}\,\mathrm{d}l. \]
The rod is attached at one of its ends; thus, we integrate along the entire length of the rod, from 0 to L.
We calculate the integral:
\[ I_{rod}= \frac{M}{L} \int_0^{L}l^2\,\mathrm{d}l = \frac{M}{L}\left [\frac{l^3}{3} \right ]_0^L = \frac{M}{L}\left [\frac{L^3}{3} \right ]=\frac{ML^2}{3}. \]
Solution of b)
We will use the law of conservation of angular momentum to determine the angular velocity with which the rod starts to rotate. We will compare two situations when the total angular momentum of the system of the bullet and the rod must be equal. We will thus obtain an equation from which we will express the angular velocity.
An angular momentum \(\vec{L}\) of a mass point with respect to a point 0 is defined as a cross product of a position vector \(\vec{r}\) and a momentum \(\vec{p}\) of a mass point.
\[\vec{L} = \vec{r} \times \vec{p}\,.\]It holds for a magnitude of the cross product:
\[L = rp\sin\varphi \,,\]where φ is the angle between the vectors.
The vector \(\vec{L}\) of angular momentum is perpendicular to a plane defined by vectors \(\vec{r}\) and \(\vec{p}\). We determine the orientation of the angular momentum using the right-hand rule: we curl the fingers to represent a motion from \(\vec{r}\) to \(\vec{p}\), the thumb then points along the direction of the vector \(\vec{L}\).
It holds for an angular momentum \(\vec{L}\) of a rigid body with respect to a fixed axis of rotation that:
\[\vec{L} = I\vec{\omega}\,,\]where I is the moment of inertia of the body with respect to the fixed axis of rotation and \(\vec{\omega}\) is the angular velocity with which the body rotates.
For the magnitude of angular momentum, we have:
\[L = I\omega\,.\]And the orientation of vector \(\vec{L}\) of angular momentum is the same as the orientation of the vector \(\vec{\omega}\) of angular velocity.
We will determine the angular momentum of the system of the bullet and the rod with respect to the point where the rod is attached.
In the beginning, the rod is at rest. The total angular momentum of the system is thus equal to the angular momentum of the bullet, which is moving at the speed v0 in a direction perpendicular to the rod. The magnitude of the radius vector \(\vec{r}\) equals the length of the rod L.
Angular momentum for the first situation is:
\[\vec {L_{1}} = \vec {r}×\vec{p}= \vec {r}×\left (m\vec{v_{0}}\right ).\]
The vector of angular momentum points out of the screen. From knowing that sine of the right angle defined by the velocity and the radius vector is 1, we get for the magnitude of the angular momentum:
\[L_{1} = Lp = Lmv_{0}.\tag{3}\]
In the second situation; we also have to consider the rotational motion around the axis. We determined the moment of inertia of the rod Irod in the solution of a). There is now the bullet stuck in the rod, we must, therefore, consider the moment of inertia of the bullet as well (we assume the bullet to be a mass point). Because the rod and the bullet are moving with the same angular velocity, we can simply sum their moments of inertia up:
\[ \vec{L_{2}} = \left(\frac{1}{3}ML^2 + mL^2\right)\vec{\omega}\,. \]
The angular momentum points out of the screen as well as in the previous situation. It holds for its magnitude:
\[ L_{2} = \left(\frac{1}{3}ML^2 + mL^2\right)\omega. \tag{4}\]Equality of the relations (3) and (4) follows from the law of conservation of angular momentum:
\[ L_{1}=L_{2}, \]
\[ mv_{0}L = \left(\frac{1}{3}ML^2 + mL^2\right)\omega. \]
We express the angular velocity \(\omega\):
\[ mv_{0} = \left(\frac{1}{3}M + m\right)L\omega, \]
\[ \omega = \frac{mv_{0}}{\left(\frac{1}{3}M + m\right)L}. \]
Rearranging the expression we get:
\[ \omega = \frac{3mv_{0}}{\left(M + 3m\right)L}. \]
Solution of c)
We will first determine the change of internal energy of the system of the bullet and the rod just before and just after the moment when the bullet hits the rod. It is equal to the difference in the total mechanical energy of the system before the hit and after it.
The potential energy of the bullet is the same before the hit and after it. The same applies to the rod. Therefore, we can focus on the kinetic energy only. In the beginning, the kinetic energy of the system equals the kinetic energy of the bullet \(E_{k_{0}}\) (the kinetic energy of the rod is equal to zero):
\[E_{k_{0}} = \frac{1}{2}mv_{0}^2.\]After the hit, the rod with the bullet stuck inside starts to rotate with an angular velocity \(\omega\). The equation for the kinetic energy of rotation \(E_k\) looks similar to the one for the kinetic energy of translation, we just consider angular velocity instead of velocity and moment of inertia instead of mass:
\[E_k = \frac{1}{2}I_{total} \omega^2,\]where \(I_{total}\) stands for the moment of inertia of the system of the bullet and the rod. Because the bullet is stuck in the rod after the hit, we determine the moment of inertia of the system \(I_{total}\) as a sum of the moment of inertia of the rod (see solution of a)) and the moment of inertia of the bullet (we consider the bullet to be a mass point). We thus get:
\[E_k = \frac{1}{2}\left(\frac{1}{3}ML^2+mL^2\right)\omega^2.\]We determine the change in internal energy as a difference of the initial kinetic energy and the final kinetic energy:
\[ \Delta U = E_{k_{0}} − E_k. \]
We can now determine the ratio of the change in internal energy of the system \(\Delta U\) to the initial kinetic energy of the system \(E_{k_{0}}\) by substituting the above relations:
\[ \frac{\Delta U}{E_{k_{0}}} =\frac{E_{k_{0}} − E_k}{E_{k_{0}}} =\frac{\frac{1}{2}mv_{0}^2−\frac{1}{2}\left(\frac{1}{3}ML^2+mL^2\right) \omega^2}{\frac{1}{2}mv_{0}^2}. \]
We substitute for the angular velocity \(\omega\) from the solution of b) and rearrange the expression:
\[ \frac{\Delta U}{E_{k_{0}}}=\frac{\frac{1}{2}mv_{0}^2−\frac{1}{6}L^2\left(M+3m\right) \frac{9m^2v_{0}^2}{\left(M + 3m\right)^2L^2}}{\frac{1}{2}mv_{0}^2} = \frac{\frac{1}{2}m−\frac{3}{2} \frac{m^2}{\left(M + 3m\right)}}{\frac{1}{2}m} = 1−\frac{3m}{\left(M + 3m\right)}. \]
We get the ratio:
\[ \frac{\Delta U}{E_{k_{0}}}= \frac{M}{\left(M + 3m\right)}. \]
Answer for a)
The moment of inertia of the rod with respect to the horizontal axis of rotation passing through one end of the rod is:
\[I_{rod}= \frac{1}{3}ML^2. \]Answer for b)
The angular velocity with which the rod starts to rotate is:
\[ \omega = \frac{3mv_{0}}{\left(M + 3m\right)L}. \]Answer for c)
The ratio of the change in internal energy of the system of the bullet and the rod \(\Delta U\) to the initial kinetic energy of this system \(E_{k_{0}}\) is:
\[ \frac{\Delta U}{E_{k_{0}}}= \frac{M}{\left(M + 3m\right)}. \]
Similar task
Try to solve the task A Projectile Hitting an End of a Rotatable Rod which is similar to this one.



