Cart
Task number: 1523
A small cart of mass m goes without sliding down an incline that leads into a cylindrical loop of radius r. From what height h must the cart go down to pass through the entire circular loop of the cylindrical surface? Neglect a moment of inertia and rolling resistance of wheels.
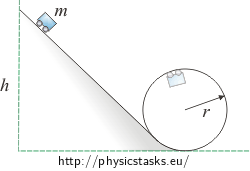
Notation
m mass of the cart r radius of cylindrical surface h = ? height of the track necessary for the cart to get through the whole cylindrical loop Analysis
The speed of the cart must be nonzero at the highest point of the loop to pass through the entire loop. At first we will find out the minimal value of this speed using Newton’s second law. The cart goes down without sliding so for solving the maximum height of the track we can use a law of conservation of mechanical energy.
Hint 1 – the speed at the highest point of the loop
Find out the minimum speed of the cart at the highest point of the loop to pass through the entire loop. Draw a picture of force vectors acting on the cart and write the equation of motion. What is magnitude of forces at the time when the cart starts to fall down?
Hint 2 – conservation of mechanical energy
Choose a zero point. Describe mechanical energy of the cart when the cart is released (1) and at the highest point of the loop (2).
Answer
The height necessary for the cart to get through the whole loop is \(h\,=\,\frac{5r}{2}\).
Total Solution
The speed of the cart must be nonzero at the highest point of the loop so that the cart can get through the entire loop. We find out the minimum value of this speed using Newton’s second law. The cart goes down without sliding so for solving the maximum height of the track we can use the law of conservation of mechanical energy.
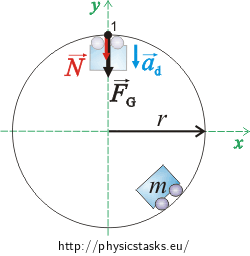
The forces acting on the cart at the highest point of the loop are \(\vec{F_G}\) – weight force and \(\vec{N}\)– normal force. Acceleration of the cart \(\vec{a_d}\) points down to the center of the loop.
The equation of motion for the cart:
\[\vec{N}+\vec{F_G}\,=\,m\vec{a_d}\]\(N\)…normal force acting on the cart
\(F_G\)…weight force acting on the cart
\(a_d\)…normal acceleration of the cart
We select a coordinate system (as shown in the figure) and write the scalar equation of motion:
\[-N-F_G\,=\,-ma_d\] \[N+mg\,=\,ma_d\]\(m\)…mass of the cart
\(g\)…gravity of Earth
When the cart starts to fall off, the loop stops acting on it and the force N will be zero. We find the minimum speed at which the cart can pass through the entire loop without falling down and staying on the loop using a condition N = 0 N.
\[mg\,=\,ma_d\] \[mg\,=\,m\frac{v_1^2}{r}\]\(v_1\)…minimum speed necessary at the highest point of the loop
\(r\)…radius of cylindrical surface
We express speed v1:
\[g\,=\,\frac{v_1^2}{r}\] \[v_1\,=\,\sqrt {gr}\tag{1}\]Let’s use the law of conservation of mechanical energy to define the demanded height. Choose a zero point. Describe mechanical energy when release the cart (1) and at the highest point of the loop (2).
\[\mathrm{ZZME:} \hspace{15px} E_{p1}\,=\,E_{p2}+E_{k2}\]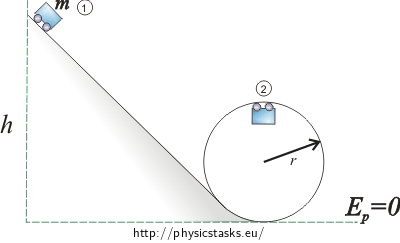
\(E_{p1}\)…potential energy of the cart at the height h
\(E_{p2}\)…potential energy of the cart at the highest point of the loop
\(E_{k2}\)…kinetic energy of the cart at the highest point of the loop
\[mgh \,=\, mg2r + \frac{1}{2}mv_1^2\]We substitute speed v1 from the equation (1):
\[mgh \,=\, mg2r + \frac{1}{2}mgr\] \[h\,=\,\frac{5r}{2}\]Answer: The height necessary for the cart to get through the whole loop is \(h\,=\,\frac{5r}{2}\).


