A Cylinder Immersed in Water
Task number: 2002
A wooden cylinder is immersed in water, 2/3 of its height submerged. How much work is necessary to take the cylinder out, so that its bottom base is lifted 20 cm above the water surface? The radius of the cylinder is 10 cm and its height is 60 cm.
Notation
r = 10 cm = 0,1 m radius of the cylinder h = 60 cm = 0,6 m height of the cylinder x = 2/3h the submerged part of the cylinder a = 20 cm = 0,2 m height to which the cylinder is lifted W = ? (J) work needed to lift up the cylinder Hint 1 - a floating cylinder
Draw a picture of the floating cylinder and the forces which are acting on it. What do you know about them?
Hint 2 - the force needed to take the cylinder out
Draw a picture of the situation when the cylinder is lifted the height x up but still partially submerged. Which forces are acting on it? How much force is needed to hold the cylinder so it won’t sink?
Hint 3 - the work needed to pull the cylinder up to the surface level
How much work is needed to lift the cylinder to the surface level? You know the force we apply when taking the cylinder out and also the path of its movement. Realize that the force is not constant but it is dependent on the height which the cylinder was taken out.
Hint 4 - the work needed to lift the cylinder above the water surface
How much work is required to lift the cylinder up from the water surface to the height a? Can you determine the total work?
Numerical calculation:
We know:
\[r\,=\,10\,\mathrm{cm}\,=\,0{,}1\,\mathrm{m},\] \[h\,=\,60\,\mathrm{cm}\,=\,0{,}6\,\mathrm{m},\] \[a\,=\,20\,\mathrm{cm}\,=\,0{,}2\,\mathrm{m},\] \[g\,=\,9{,}81\,\mathrm{m \cdot s^{-2}},\] \[\rho\,=\,1000\,\mathrm{kg\,m^{-3}}.\]We search for:
\[W\,=\,?,\] \[W\,=\,\frac{2}{3}\rho \pi r^2gh\left(\frac{1}{3}h+a\right),\] \[W\,=\,\frac {2}{3}\cdot1000{\cdot}3{,}14{\cdot} 0{,}1^2{\cdot}9{,}81{\cdot} 0{,}6\cdot\left(\frac{1}{3}\cdot0{,}6+0{,}2\right)\,\mathrm{J},\] \[W\,=\,49\,\mathrm{J}.\]Complete solution
We first think of the forces acting on the cylinder when it is floating and determine what holds for these forces.
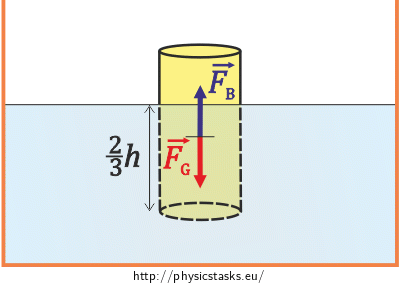
\(\vec{F_G}\)…the force of gravity
\(\vec{F_B}\)…the buoyant force
\(h\)…height of the cylinder
As the cylinder is floating, the force of gravity is in balance with the buoyant force.
It holds:
\[F_G\,=\,F_B,\] \[mg\,=\,V_{p}\rho g,\]\(m\)…mass of the cylinder,
\(g\)…acceleration of gravity,
\(V_p\)…volume of the submerged part of the cylinder,
\(\rho\)…density of water.
We use the density of the cylinder and its volume to express its mass:
\[\rho_w V_cg\,=\,V_{p}\rho g,\]\(\rho_w\)…density of wood,
\(V_c\)…volume of the cylinder.
We write the equation for the volume of the cylinder and its submerged part using its height and the area of its base and we determine the relation between the density of wood and the density of water:.
\[\rho_wShg\,=\,\rho S\frac{2}{3}h g,\] \[\rho_w\,=\,\frac{2}{3}\rho.\tag{1}\]We now analyse the situation when the cylinder is lifted the height x out of water.
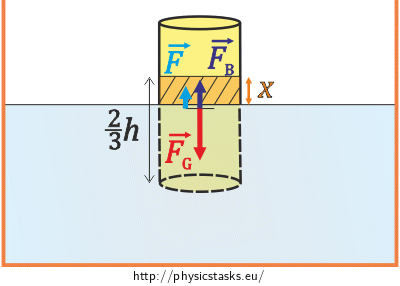
\(\vec{F_G}\)…force of gravity
\(\vec{F_B^{'}}\)…buoyant force
\(\vec{F}\)…force we apply when taking the cylinder out
If we take the cylinder a height x out of water, the submerged volume reduces and therefore also the magnitude of the buoyant force acting on it decreases. Supposing the steady motion when taking the cylinder out, we have to hold it with a force whose magnitude is equal to the decrease of the buoyant force.
\[F\,=\,V_x\rho g=S\rho gx\tag{2}\]The force we apply when taking the cylinder out is proportional to the height it was took out.
A variable force is acting in the direction of displacement. The work can be calculated from the relation:
\[W_1\,=\,\int_{x_1}^{x_2}{F\mathrm{d}x}.\]We substitute from equation (2) for F, the cylinder is being taken out from x1 = 0 to x2 = 2/3 h.
\[W_1\,=\,\int_{0}^{\frac{2}{3}h}{S\rho gx\mathrm{d}x}\,=\,S\rho g\int_{0}^{\frac{2}{3}h}{x\mathrm{d}x},\] \[W_1\,=\,S\rho g\left[\frac{x^{2}}{2}\right]_{0}^{\frac{2}{3}h}\,=\,S\rho g\frac{2}{9}h^2,\] \[W_1\,=\,\frac{2}{9}\pi r^2\rho h^2g.\tag{3}\]Note: Graphic solution
The work needed to takke the cylinder out of the water can be also determined from the graph of the force F dependence on the height x the cylinder was lifted up.
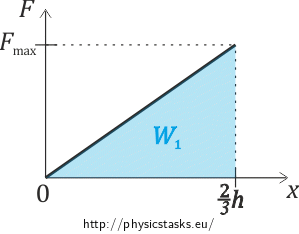
If the cylinder is floating in water, then x = 0 and force F = 0. When taken out to the surface level, \(x\,=\,\frac{2}{3}h\). We must hold the cylinder with force Fmax which is equal to its weight.
\[F_{max}\,=\,F_G\,=\,mg\,=\,\rho_w Vg\,=\,\frac{2}{3}\rho \pi r^2hg\]The force is equal to the area under the curve. Thus it holds that:
\[W_1\,=\,\frac{F_{max}\frac{2}{3}h}{2}=\frac{2}{9}\rho \pi r^2h^2g.\]The work needed to lift the cylinder the height a above the water surface is equal to the increase of the potential energy of the cylinder.
\[W_2\,=\,\Delta E_p\] \[W_2\,=\,mga\] \[W_2\,=\,\rho_wV_cga\]We substitute for \(\rho_w\) from equation (1):
\[W_2\,=\,\frac{2}{3}\rho \pi r^2 hga.\tag{4}\]The total work is equal to the sum of the work needed to take the cylinder out of the water and from the work done when lifting it above the surface:
\[W\,=\,W_1+W_2,\] \[W\,=\,\frac{2}{9}\rho \pi r^2h^2g+\frac{2}{3}\rho \pi r^2 hga\,=\,\frac{2}{3}\rho \pi r^2gh\left(\frac{1}{3}h+a\right).\] \[W\,=\,\frac {2}{3}\cdot1000{\cdot}3{,}14{\cdot} 0{,}1^2{\cdot}9{,}81{\cdot} 0{,}6(\frac{1}{3}\cdot0{,}6+0{,}2)\,\mathrm{J}\] \[W\,=\,49\,\mathrm{J}\]Answer
The work needed for lifting the cylinder 20 cm up is: \[W=\frac{2}{3}\rho \pi r^2gh\left(\frac{1}{3}h+a\right)\,=\,49\,\mathrm{J}.\]




