Mouse and Cat
Task number: 927
A mouse is moving in a straight line with a constant velocity \[\vec{v}_m\,=\,(3,\,-2)\,\mathrm{m\cdot s^{-1}}\] from point \[A = [0,\,1]\,\mathrm{m}\] and a cat is moving in a straight line with a constant velocity \[\vec{v}_c\,=\,(4,\,1)\,\mathrm{m\cdot s^{-1}}\] from point \[B = [0,\,-1]\,\mathrm{m}\] .
a) Determine the place where their paths will intersect. Are they going to meet there?
b) Determine the time when the cat and mouse are the nearest.
c) Determine the minimum distance between the cat and the mouse.
Note: Parametric equations should be written in the form of e.g.
\[y\,=\,1\,\mathrm{m} \,-\, 2\,\mathrm{m\cdot s^{-1}}\cdot t\]For simplicity of the notation formulas are unitless.
Hint 1: Part (a): The Intersection of Cat’s and Mouse’s Trajectories
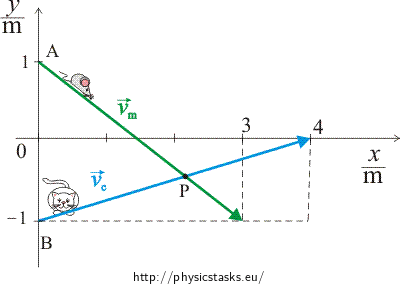
Mark the initial position of the cat and mouse into coordinate system. Can you draw the lines of their movements if you know the directions of their velocities? If your drawing was accurate the intersection of the lines can be easily subtracted from the picture. Intersection point can be also solved by writing down the parametric equations of the cat’s and mouse’s trajectories. One of its points and directions is known in each of the lines.
Hint 2: Part (a): Cat’s and Mouse’s Meeting
At what time will the mouse and the cat arrive at the point? Is it the same time?
Hint 3: Relationship Between Time and Cat‘s and Mouse’s Distance
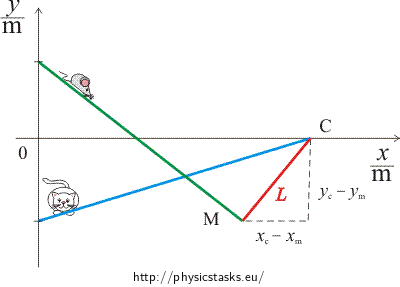
Do you know the relationship between time and the cat’s and the mouse’s coordinates? Can you express the time-dependence of their distance between them? Formula for distance of two points can be easily derived from the picture 2 or you can look into the mathematical tables.
Hint 4 Part (b): The Time When the Mouse and the Cat are the Nearest
Now you know the time-dependence of the distance between the cat and the mouse. How do you find a minimum of this function?
Hint 5: Part (c): Minimum Distance Between the Cat and the Mouse
Now you know the time when the mouse and the cat are the nearest and also the time-dependence of their distance. How do you determinate the minimum distance?
Complete Solution
a)
Graphical solution:
Picture 1:
\[A\,=\,[0,\,1]\,\mathrm{m}\] \[v_m\,=\,(3,\,-2)\,\mathrm{m\cdot s^{-1}}\] \[B\,=\,[0,\,-1]\,\mathrm{m}\] \[v_c\,=\,(4,\,1)\,\mathrm{m\cdot s^{-1}}\] Numerical Solution:
Parametric equations of the mouse line:
\[x_m\,=\,0+3t_m\] \[y_m\,=\,1\,-\,2t_m\]Equation of the mouse trajectory is obtained by eliminating parameter tm.
\[t_m\,=\,\frac{x_m}{3}\]Mouse trajectory:
\[y_m\,=\,1\,-\,2\frac{x_m}{3}\] \[3y_m\,=\,3\,-\,2x_m\]Parametric equations of the cat’s line:
\[x_c\,=\,0\,+\,4t_k\] \[y_c\,=\,-1\,+\,t_k\]Equation of the cat‘s trajectory is obtained by eliminating the parameter tc.
\[t_c\,=\,\frac{x_k}{4}\]Cat’s trajectory:
\[y_c\,=\,-1\,+\,\frac{x_c}{4}\] \[4y_c\,=\,x_c\,-\,4\]Intersection point of the trajectories:
\[x_m \,=\, x_c \,=\, x\] \[y_m \,=\, y_c \,=\, y\]Two equations in two unknowns x and y is solved:
\[3y \,=\, 3\,-\,2x\tag{1}\] \[4y \,=\, x\,-\,4\tag{2}\]From (2):
\[x \,=\, 4y \,+\, 4\,.\]is substituted to (1):
\[3y \,=\, 3 \,-\, 8y \,-\, 8\,.\]Hence:
\[y\,=\,-\frac{5}{11}\,,\] \[x\,=\,\frac{24}{11}\,.\]Coordinates of the intersection point P:
\[P \,=\, \left[\frac{24}{11},\,-\frac{5}{11}\right]\,\mathrm{m}\,.\]Mouse is at the point P
\[\left[\frac{24}{11},\,-\frac{5}{11}\right]\,\mathrm{m}\]at the time
\[t_m \,=\, \frac{x}{3} \,=\, \frac{24 }{11{\cdot}3} \,\mathrm{s} \, =\, \frac{8}{11}\,\mathrm{s}.\]Cat is at point P
\[\left[\frac{24}{11},\,-\frac{5}{11}\right]\,\mathrm{m}\]at the time
\[t_c\, =\, \frac{x}{4} \,=\, \frac{24}{11 {\cdot} 4} \,\mathrm{s} = \frac{6}{11}\,\mathrm{s}.\]Arrival times are different, it means that they don’t meet at point P.
b)
The relationship between time and cat’s and mouse’s distance L(t) can be derivated from the picture 2.
Picture 2:
\[x_c\,-\,x_m\,=\,4t\,-\,3t\,=\,t\] \[y_c\,-\,y_m\,=\,t-1\,+\,2t-1\,=\,3t-2\]By using Pythagorean Theorem:
\[L(t)\,=\,\sqrt{(x_c\,-\,x_m)^{2}+(y_c\,-\,y_m)^{2}}=\sqrt{10t^{2}\,-12t\,+\,4}\]To find the time, when the cat and the mouse are the nearest, is to find a minimum of a function L(t).
We’ll find the derivative of the function L(t) with respect to time t and then its extreme:
\[\frac{\mathrm{d}L}{\mathrm{d}t}\,=\,\frac{1}{2}\,\frac{20t_{min}\,-12}{\sqrt{10t_{min}^{2}\,-12t_{min}\,+4}}\,=\,0\] \[20t_{min}\,-\,12 \,=\, 0\] \[t_{min}\,=\,\frac{3}{5}\,\mathrm{s}\]The time when the mouse and the cat are the nearest:
\[t_{min} \,=\, 0.6\,\mathrm{s}\,.\]c)
The time when the mouse and the cat are the nearest:
\[t_{min}\,=\, 0.6 \,\mathrm{s}\,.\]By substituting this value into the function L(t) we get the smallest distance of the mouse and the cat.
\[L_{min} \,=\,\sqrt{10t_{min}^{2}-12t_{min}\,+\,4} \] \[L_{min} \,=\, \sqrt{10{\cdot}0.6^{2}\,-12{\cdot}0.6\,+4}\,\mathrm{m}\,=\,\sqrt{0.4}\,\mathrm{m} \,=\, 0.63 \,\mathrm{m} \]Answers
a) Paths of the mouse and the cat will intersect at point:
\[P \,=\, \left[\frac{24}{11},\,-\frac{5}{11}\right]\,\mathrm{m}\,.\]The mouse and the cat will not meet at point P, because the mouse will arrive at
\[t_m\,=\,\frac{8}{11}\,\mathrm{s}\]and the cat will arrive at
\[t_k\,=\,\frac{6}{11}\,\mathrm{s}\,.\]b) The time when and the cat are the nearest:
\[t_{min} \,=\, 0.6 \,\mathrm{s}\,.\]c) The minimum distance between the cat and the mouse:
\[L_{min}\, =\, \sqrt{10t_{min}^{2}\,-\,12t_{min}\,+\,4} \,=\, 0.63\,\mathrm{m}\,.\]