Crane Lifting a Panel
Task number: 1981
A construction panel with dimensions of 2.4 m by 1.2 m and a thickness of 15 cm is made out of concrete reinforced with steel rods such that the mean density of the material is 3 000 kg·m−3. It is lightened with five holes in the direction of its thickness, each with a diameter of 6 cm.
a) Determine the volume of material in the panel and its mass.
b) What force does the crane need to exert to lift the panel?
c) How much work will the crane do by lifting the panel to a height of 42 m?
d) How long will it take to lift the panel if the velocity of lifting is 0.25 m·s−1? What power does the crane produce in this scenario?
e) The electric engines produce work with an efficiency of 70 %. What input power do we have to provide in order to lift the panel?
f) The maximum allowable stress for a steel rope is 100 MPa and the crane has a load capacity of at most 5 tons. What is the minimal diameter of the rope?
Given values
a = 2.4 m dimension of the construction panel b = 1.2 m dimension of the construction panel c = 15 cm dimension of the construction panel ρ = 3 000 kg·m−3 mean density of concrete reinforced with steel rods r0 = 6 cm radius of the holes h = 42 m height to which we need to lift the panel v = 0.25 m·s−1 velocity of lifting η = 70 % efficiency of the electric engine σ = 700 MPa allowable stress for a steel rope M = 5 t maximum load capacity of the crane m = ? mass of the panel V = ? volume of the panel F = ? force by which the crane must lift the panel W = ? work done by the crane t = ? time needed to lift the panel P' = ? output power of the crane P = ? input power of the crane d = ? minimal diameter of the rope Hint a1) – panel volume
Draw a picture of the panel with holes.
What formula can we apply to calculate the volume of a cuboid?
How will the five holes affect the volume of the cuboid?
Hint a2) – Mass of the panel
Now you know the volume and the density of the panel is given. How can you calculate its mass?
Hint b) – Force
Draw a picture of the situation and mark the forces acting upon the panel.
Assume the crane lifts the panel in a uniform linear motion. How large is the total force acting upon the panel? How large is the force with which the crane acts upon the panel?
Hint c) – Work done by the crane
The crane acts upon the panel with a constant force on a given path and the direction of the force aligns with the direction of displacement.
How can you calculate the work done by the crane in this scenario?
Hint d1) – Duration of the lift
You know the displacement and the velocity of lifting, which is constant. The duration of the lift can then be easily expressed.
Hint d2) – Power of the crane
You know the work done by the crane and the time in which it is done.
What relation holds for the calculation of power?
Hint e) – Input power of the engine
Input power of the engine describes the energy it receives in a unit of time. Due to unavoidable losses caused by various resistances against the movement, the output power of every device is lower than its input power. Efficiency then describes the ratio of the output power and the required input power. Efficiency is a dimensionless quantity describing how close the process taking place in the device is to an ideal process. The input power can then be expressed using efficiency and output power.
Hint f1) – Stress in the rope
The allowable load can be also expressed as the maximum stress that can be exerted onto the rope. How is stress defined?
Hint f2) – Diameter of the rope
The force acting upon the rope is equal to the weight of the load. You know the maximum allowable stress for the rope. You can easily express the area of the cross section of the rope and from there its diameter.
Numerical solution
a) Panel volume and mass
\[a\,=\,2.4\, \mathrm{m}\] \[b\,=\,1.2\, \mathrm{m}\] \[c\,=\,15\, cm=0.15\, \mathrm{m }\] \[r_{0}\,=\,3\, \mathrm{cm}\,=\,0.03\, \mathrm{m}\] \[\rho\,=\,3\,000\, \mathrm{kg \cdot m^{-3}}\]
\[V\,=\,abc\,-\,5\pi r_0^2 c\] \[V\,=\,\left(2.4{\cdot}1.2{\cdot} 0.15-5{\cdot}3.14{\cdot}0.03^{2}\cdot0.15\right)\,\mathrm{m^3}\] \[V\,=\,\left(0.432-0.0021\right)\, \mathrm{m^3}\] \[V\,=\,0.4299\, \mathrm{m^3}\,\dot=\,0.43\ \mathrm{m^3}\] \[m\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)\] \[m\,=\,3\,000{\cdot} 0.15\left(2.4{\cdot} 1.2\,-\,5{\cdot} 3.14{\cdot} 0.03^2\right)\,\mathrm{kg}\] \[m\,=\,1\,290\, \mathrm{kg}\]b) Force with which the crane lifts the panel
\[m\,=\,1\,290\, \mathrm{kg}\] \[g\,=\,9.81\, \mathrm{m \cdot s^{-2}}\]
\[F\,=\,mg\] \[F\,=\,1\,290{\cdot}9.81\,\mathrm{N}\] \[F\,=\,12\,655\, \mathrm{N}\,\dot=12.7\ \mathrm{kN}\]c) Work performed by the crane
\[F\,=\,12\,655\, \mathrm{N}\] \[s\,=\,42\, \mathrm{m}\]
\[W\,=\,Fs\] \[W\,=\,12\,655{\cdot}42\,\mathrm{J}\] \[W\,=\,531\,510\, \mathrm{J}\,\dot=531.5\ \mathrm{kJ}\]d1) Duration of the lift
\[s\,=\,42\, \mathrm{m}\] \[v\,=\,0.25\, \mathrm{m \cdot s^{-1}}\]
\[t\,=\,\frac{s}{v}\] \[t\,=\,\frac{42}{0.25}\,\mathrm{s}\] \[t\,=\,168\, \mathrm{s}\,=\,2\,\mathrm{min}\,48\, \mathrm{s}\]d2) Output power of the crane
\[W\,=\,531\,510\, \mathrm{J}\] \[t\,=\,168\, \mathrm{s}\]
\[P^{'}\,=\,\frac{W}{t}\] \[P^{'}\,=\frac{531\,510}{168}\,\mathrm{W}\] \[P^{'}\,=\,3\,164\, \mathrm{W}\,\dot=\,3.2\ \mathrm{kW}\]e) Input power of the crane
\[P^{'}\,=\,3\,164\, \mathrm{W}\] \[\eta\,=\,0.7\]
\[P\,=\,\frac{P^{'}}{\eta}\] \[P\,=\,\frac{3\,164}{0.7}\,\mathrm{W}\,=\,4\,520\, \mathrm{W}\,\dot=\,4.5\ \mathrm{kW}\]f) Diameter of the rope
\[M\,=\,5\, \mathrm{t}\,=\,5\,000\, \mathrm{kg}\] \[g\,=\,9.81\, \mathrm{m \cdot s^{-2}}\] \[\sigma\,=\,100\, \mathrm{MPa}\,=\,10^{8}\,\mathrm{Pa}\]
\[d\,=\,\sqrt{\frac{4Mg}{\sigma\pi}}\] \[d\,=\,\sqrt{\frac{4{\cdot}5\,000{\cdot}9{,}81}{10^{8}\cdot3{,}14}}\,\mathrm{m}\,=\,0.025\,\mathrm{m}\,=\,2.5\, \mathrm{cm}\]Answer
a) The volume of the panel is \[V\,=\,abc\,-\,5{\pi}r_{0}^{2}c\,=\,0.4299\,\mathrm{m^3}\,\dot=\,0.43\ \mathrm{m^3}.\]
The mass of the panel is \[m\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)\,=\,1\,290\,\mathrm{kg}.\]
b)The crane must lift the panel with a force equal to \[F\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)g\,=\,12\,655\,\mathrm{N}\,\dot=\,12.7\, \mathrm{kN}.\]
c) While lifting the panel to a height of 42 m, the crane performes work equal to \[W\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)gs\,=\,531\,510\,\mathrm{J}\,\dot=\,531.5\ \mathrm{kJ}.\]
d) The time required for the crane to lift the panel with the velocity of 0.25 m·s-1 is \[t\,=\,\frac{s}{v}\,=\,2\,\mathrm{min}\,48\,\mathrm{s}.\]
In this scenario the output power of the crane is equal to \[P^{'}\,=\,\frac {\rho c\left(ab\,-\,5\pi r_0^2\right)gs}{t}\,=\,3\,164\, \mathrm{W}\,\dot=\,3.2\ \mathrm{kW}.\]
e) The input power we must supply is equal to \[P\,=\,\frac {\rho c\left(ab\,-\,5\pi r_0^2\right)gs}{\eta t}\,=\,4\,520\, \mathrm{W}\,\dot=\,4.5\ \mathrm{kW}.\]
f) The minimal diameter of the rope ought to be \[d\,=\,\sqrt {\frac{4Mg}{\sigma \pi}}\,=\,2.5\, \mathrm{cm}.\]
Overall solution of point a) – Volume and mass of the panel
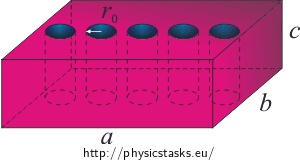
We can look up the formula for the volume of a cuboid in mathematical tables:
\[V\,=\,abc\,.\]V……volume of cuboid
a, b, c…dimensions of cuboid
When a part is cut out of the cuboid, the final volume is decreased by the volume of said part.
In our case, there are five holes shaped like cylinders with the given diameter. The volume of each cylinder is equal to:
\[V\,=\,\pi r_0^2 c\,.\]V…volume of the removed part
r0…radius of the hole
c…height of the cylinder (hole)
The height of the cylinder is equal to the height of the panel.
We subtract the volumes of the cylinders from the total volume of the panel. We get:
\[V\,=\,abc\,-\,5\pi r_0^2 c\,.\] \[V\,=\,\left(2.4{\cdot} 1.2{\cdot}0.15\,-\,5{\cdot} 3.14{\cdot} 0.03^2{\cdot}0.15\right)\,\mathrm{m^3},\] \[V\,=\,0.4299\, \mathrm{m^3}\,\dot=\,0.43\ \mathrm{m^3}.\]For a given volume and density it holds for mass that:
\[m\,=\,\rho V\,.\]m… mass of the panel
ρ… density of the panel
V… volume of the panel
We substitute for volume from relation (1):
\[m\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)\,.\] \[m\,=\,3\,000\,\cdot 0.15\left(2.4{\cdot} 1.2\,-\,5{\cdot} 3.14{\cdot} 0.03^2\right)\,\mathrm{kg},\] \[m\,=\,1\,290\, \mathrm{kg}.\]Answer:
The panel volume is \[V\,=\,0.4299\, \mathrm{m^3}\,\dot=\,0.43\ \mathrm{m^3}.\]
The panel mass is \[m\,=\,1\,290\,\mathrm{kg}.\]
Overall solution of point b) – Force with which the crane lifts the panel
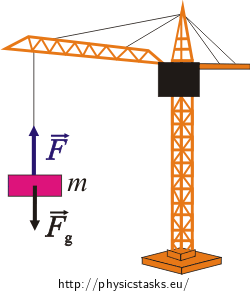
\(\vec{F}\)… force with which the crane acts upon the panel
\(\vec{F}_\mathrm{g}\)… gravitational force
The net force acting upon the panel during a uniform linear motion is equal to zero. The force with which the crane acts upon the panel is equal to the gravitational force acting upon the panel.
\[F\,=\,F_\mathrm{g}\,=\,mg.\]F… force with which the crane acts upon the panel
Fg… gravitational force
m… mass of the panel
g… acceleration of gravity
We know the mass of the panel m from the previous paragraph and the value of the acceleration of gravity can be found in the tables.
\[g\,=\,9.81\,\mathrm{m \cdot s^{-2}}.\]We substitute for m from relation (2):
\[F\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)g.\] \[F\,=\,1\,290\,\cdot9.81\,\mathrm{N},\] \[F\,=\, 12\,655\, \mathrm{N}\,\dot=\,12.7\ \mathrm{kN}.\]Answer: The crane must lift the panel with force equal to \[F\,=\,12\,655\,\mathrm{N}\,\dot=\,12.7\,\mathrm{kN}.\]
Overall solution of point c) – Work done by the crane
When a constant force acts in the direction of the displacement of the panel, we can calculate the work with the relation:
\[W\,=\,Fs\,.\]W… work done
F… force with which the crane acts upon the panel
s… path on which the crane acts with the force F
We substitute for F from relation (3):
\[W\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)gs\,.\] \[W\,=\,12\,655\,\cdot42\,\mathrm{J},\] \[W\,=\,531\,510\,\mathrm{J}\,\dot=\,531.5\ \mathrm{kJ}.\]Answer: When lifting the panel to the height 42 m, the crane performs work equal to \[W\,=\,531\,510\,\mathrm{J}\,\dot=\,531.5\ \mathrm{kJ}.\]
Overall solution of point d) – Duration of the lift, output power of the crane
The motion of the panel is uniform and linear; therefore, its velocity can be expressed using the relation:
\[v\,=\,\frac{s}{t}\,.\]v… velocity
s… displacement
t… time
From where we get for time t:
\[t\,=\,\frac{s}{v}\,.\] \[t\,=\,\frac{42}{0.25}\,\mathrm{s},\] \[t\,=\,168\, \mathrm{s}\,=\,2\, \mathrm{min}\,48\, \mathrm{s}.\]Power is the work done in a unit of time. When we express this with a relation, we get:
\[P^{'}\,=\,\frac{W}{t}\,.\]P'… power of the crane
W… work done
t… time in which the work is done
We calculated the work W and the duration of the lift in the previous paragraphs.
We substitute for work W from relation (4):
\[P^{'}\,=\,\frac {\rho c\left(ab\,-\,5\pi r_0^2\right)gs}{t}\,.\] \[P^{'}\,=\,\frac{531\,510}{168}\,\mathrm{W},\] \[P^{'}\,=\,3\,164\, \mathrm{W}\,\dot=\,3.2\ \mathrm{kW}.\]Answer:
The crane lifts the panel with the speed of 0.25 ms-1 for the time \(t\,=\,2\,\mathrm{min}\,48\,\mathrm{s}.\)
In this case the output power of the crane is \(P^{'}\,=\,3\,164\, \mathrm{W}\,\dot=\,3.2\, \mathrm{kW}.\)
Overall solution of point e) – Input power of the crane
The mathematical expression of the relation for efficiency:
\[\eta=\frac{P^{'}}{P}\]η… efficiency
P'… output power of the engine
P… input power of the engine
We express the unknown input power needed to lift the panel by multiplying the equation with the input power P and then dividing it with efficiency \(\eta\).
We obtain:
\[P\,=\,\frac{P^{'}}{\eta}\,.\]We substitute for P' from relation (5):
\[P\,=\,\frac {\rho c\left(ab\,-\,5\pi r_0^2\right)gs}{\eta t}\,.\] \[P\,=\,\frac{3\,115}{0.7}\,\mathrm{W},\] \[P\,=\,4\,450\, \mathrm{W}\,\dot=\,4.5\ \mathrm{kW}.\]Answer: We need to supply the input power of \(P\,=\,4\,450\, \mathrm{W}\,\dot=\,4.5\ \mathrm{kW}\).
Overall solution of point f) – Diameter of the rope
The allowable load can be also expressed as the maximum stress that can be exerted onto the rope.
Normal stress is the quotient of a force F and an area S upon which the force acts:
\[\sigma \,=\,\frac{F}{S}\,.\]σ… stress
F… force
S… area of the cross section of the rope
The relation for weight is:
\[F\,=\,Mg\,.\]We substitute into relation (7):
\[\sigma \,=\, \frac {Mg}{S}\,.\]σ… stress
M… load capacity of the rope
g… acceleration of gravity
S… area of the cross section of the rope
From here:
\[S\,=\, \frac {Mg}{\sigma}\,.\]The cross section of the rope is a circle. For the area of a circle it holds that:
\[S\,=\,\pi \frac {d^2}{4}\,.\]d… diameter of the rope
We substitute into relation (8):
\[\pi \frac {d^2}{4}\,=\,\frac{Mg}{\sigma}\,.\]From here we rearrange the expression to get the unknown diameter:
\[d\,=\,\sqrt {\frac{4Mg}{\sigma \pi}}\,.\] \[d\,=\,\sqrt{\frac{4\,\cdot\,5\,000\,\cdot9.81}{10^{8}\cdot3.14}}\,\mathrm{m},\] \[d\,=\,0.025\, \mathrm{m}=2.5\, \mathrm{cm}.\]Answer: The smallest allowed rope diameter is d = 2.5 cm.




