A box on an inclined plane with a pulley II
Task number: 1518
Over what time box of mass m1 goes down inclined plane of the length s with angle α bound by rope over the pulley with bucket of mass m2? Ratio m1/m2 is such that motion is going on down the inclined plane. Omit friction and the mass of the rope. Consider pulley homogenous cylinder of mass m3 and radius R.
Notation
Familiarize with solution of task A box on an inclined plane with a pulley, which solves the same problem only omits moment of inertia of the pulley.
Hint 1
How method shown in the task A box on an inclined plane with a pulley, changes if we consider moment of inertia of the pulley nonzero? Changes somehow force effect? Draw all acting forces into the picture and assemble equations of motion for the box, the bucket and the pulley.
Hint 2
Express resultant moment on the pulley to its center in the equation (3). Then rewrite the equation in scalar form and substitute for moment of inertia and angular acceleration so that it contains acceleration of the box a.
Hint 3
Total all equations of motion and express acceleration a.
Hint 4
What kind of motion it is? Count time which box needs to travel track s from kinematics of this motions type.
COMPLETE SOLUTION
Forces acting in this situation are drawn in the picture down:
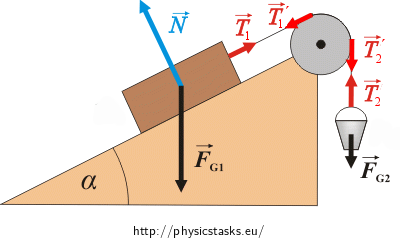
For magnitude of forces spin the pulley stands:
\[T'_1\,=\,T_1\] \[T'_2\,=\,T_2\]To spin the pulley is obvious that:
\[T_1\,\neq\,T_2\]Equations of motion for the box and the bucket are almost the same as in the task A box on an inclined plane with a pulley, only in case of the box there is force T1 and in case of the bucket force T2 instead of force T:
\[m_1gsin{\alpha}\,-\,T_1\,=\,m_1a\tag{1}\] \[T_2\,-\,m_2g\,=\,m_2a\tag{2}\]where a is acceleration of the box (and bucket) and g gravitational acceleration. Method of determination these two equations is the same as in the task A box on an inclined plane with a pulley, therefore isn’t written here in detail.
Because we consider rotational motion of the pulley (or rather its moment of inertia) is necessary write the third equation of motion for the pulley. Equation of motion for rotation motion around the fixed axis has this form:
\[\vec{M}\,=\,J\vec{\varepsilon}\tag{3}\]where M is resultant moment on object to the point, J moment of inertia of the rotating object (pulley) around the axis trough the point and ε angular acceleration. We have to determine these three quantities.
We can write for resultant moment rotating the pulley:
\[\vec{M}\,=\,\vec{R}{\times}\vec{T'_1}\,+\,\vec{R}{\times}\vec{T'_2}\tag{4}\]where R is radius of the pulley. We determine orientation of the moments of forces T1' and T2' using right-hand rule to rewrite equation (4) in scalar form. The moment of force T1' is heading in front of the projection according this rule and we’re writing it with positive sign according to agreement, while the moment of force T2' is heading behind the projection and we’re considering it negative. Scalar form of the equation (4) looks like this:
\[M\,=\,RT'_1\,-\,RT'_2\,=\,R(T'_1\,-\,T'_2)\tag{5}\]We mentioned that magnitudes of forces with acute and without it are equal already in the first hint so for magnitude forces without acute could be written:
\[M\,=\,R(T_1\,-\,T_2)\tag{6}\]Pulley is homogenous cylinder with radius R according to assignment and its moment of inertia J around the axis through its center is simply:
\[J\,=\,\frac{1}{2}m_3R^2\tag{7}\]Finally angular acceleration can be expressed by “usual” acceleration as:
\[\varepsilon\,=\,\frac{a}{R}\tag{8}\]where a is acceleration of the box.
By substitution expressions (6) to (8) ) in scalar form of equation (3) dwe gain equation of motion for rotation motion in form:
\[(T_1\,-\,T_2)R\,=\,\frac{1}{2}m_3R^2\frac{a}{R}\tag{9}\] \[T_1\,-\,T_2\,=\,\frac{1}{2}m_3a\tag{10}\]By total equations (1), (2) and (10) we gain:
\[m_1g\sin{\alpha}\,-\,m_2g\,=\,m_1a\,+\,\frac{1}{2}m_3a\,+\,m_2a\tag{11}\]By modification also gain:
\[a\,=\,g\frac{m_1\sin{\alpha}\,-\,m_2}{m_1\,+\,m_2\,+\,\frac{m_3}{2}}\tag{12}\]Acceleration of the box given by expression (12) is constant in the time so box moves by equally accelerated motion. For its tracks stands:
\[s\,=\,\frac{1}{2}at^2\,\Rightarrow\,t\,=\,\sqrt{\frac{2s}{a}}\tag{13}\]By substitute acceleration a from equation (10) we gain for unknown time:
\[t\,=\,\sqrt{\frac{2s}{a}}\,=\,\sqrt{\frac{2s}{g}\frac{m_1\,+\,m_2\,+\,\frac{m_3}{2}}{m_1\sin{\alpha}\,-\,m_2}}\tag{14}\]Answer
For unknown time t, in which the box travels on inclined plane track s, stand:
\[t\,=\,\sqrt{\frac{2s}{g}\frac{m_1\,+\,m_2\,+\,\frac{m_3}{2}}{m_1\sin{\alpha}\,-\,m_2}}\]


