Orlik Dam

Task number: 932

Orlik Dam is the largest dam in the Czech Republic conserning the capacity of water which the dam contains. The heel of the dam is 275 meters above the sea level, maximum allowed height of the water level is 354 meters above the sea level. The area of the dam is approximetly 2730 ha.

a) During the flood in 2002 the maximum allowed height of water level was exceeded by 2 meters. Figure out what pressure was in the water near the heel of the dam.

b) In time of a critical flood flow the inflow into the dam was 4400 m³/s where outflow of the dam was 3100 m³/s. How long it would take the water level in the dam to rise 1 more meter in this situation. (Consider that the rising of the water level does not affect the area of the dam.)

Notation:

h₀ = 2 m	Height by which the maximum allowed height of water level was exceeded
h₁ = 354 m.a.s.l.	Water level altitude
h₂ = 275 m.a.s.l.	Heel of the dam altitude
S = 2730 ha = 27 300 000 m²	Area of the dam
h´ = 1 m	Rise of the water level
p = ?	Resultant pressure

Data from the physical tables:
g = 10 N/kg	Number we have to multiply the mass with to get the gravitational force
ρ = 1000 kg/m³	Density of water
p_a = 101.325 kPa	Value of standard atmospheric pressure

Hint 1 – task a)
What is the resultant pressure at the bottom of the dam? What else affects the pressure?
Solution of Hint 1
The pressure at the bottom of the dam is the sum of atmospheric pressure p_a and hydrostatic pressure p_h:
\[p\,=\,p_a\,+\,p_h\tag{1}\]
Atmostpheric pressure is caused by the gravitation of air column above the surface of the dam, hydrostatic pressure caused by the gravitation of water column above the bottom of the dam.
Hint 2 – task a)
What values does the atmospheric pressure approximetly reach?
Solution of Hint 2
The value of standard atmospheric pressure is defined as:
\[ p_a\,=\,101.325\,\mathrm{kPa}\,=\,101 325\,\mathrm{Pa}\,.\tag{2}\]
For our calculation, we get by with the approximative value of 100 000 Pa.
Hint 3 – task a)
How can we figure out the hydrostatic pressure? What was the maximal depth of the water by the dam during the floods?
Solution of Hint 3
There is a formula for hydrostatic pressure:
\[p_h\,=\,h{\rho}g,\tag{3}\]
where h is the depth of the water, ρ the density of the liquid and g = 10 N/kg (number we have to multiply the mass with to get the gravitational force).

Maximal depth is the difference of two altitudes plus the height of the risen water level (2 meters):
\[h=\left(\left(h_{1}-h_2\right)\,+\,h_0\right)=\left(\left(354-275\right)+2\right)\,\mathrm{m}\,=\,81\,\mathrm{m}\,.\tag{4}\]
Hint 4 – task a)
Substitute into the formula (1) from formulas (2) and (3) and figure out the pressure p.
Solution of Hint 4
From formulas (1), (2) and (3) we get:
\[ p=p_a+\left(\left(h_{1}-h_2\right)+h_0\right){\rho}g\,,\] \[ p=\left(100 000+\left(\left(354-275\right)+2\right){\cdot}1000{\cdot}10\right)\,\mathrm{Pa}=910 000\,\mathrm{Pa}\,,\] \[ p= 910 \,\mathrm{kPa}\,.\]
Hint 5 – task b)
What is the gain in the volume of the water in the dam when water level rose about 1 meter?

The situation is depicted in the following picture:
Solution of Hint 5
If the water level rises by the height h′, the volume of water in the dam will increase:

V = S·h′
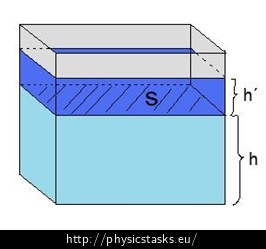
Hint 6 – task b)
How many cubic meters of water will increase in the dam in one second? How long would it take to gain the volume V? (Try to solve it by cross-multiplication.)
Solution of Hint 6
The water increase in one second is (4400-3100) m³, hence:

1 s... 1300 m³

x s... S·h′

With numbers:
\[ x=\frac{S{\cdot}h'{\cdot}1}{1300}\mathrm{s}=\left(\frac{27\,300\,000{\cdot}1{\cdot}1}{1300}\right)\,\mathrm{s}=21\,000\,\mathrm{s}\,\dot=5.8\,\mathrm{h}\,. \]
Complete solution
Task a):

The pressure at the bottom of the dam is the sum of atmospheric pressure p_a and hydrostatic pressure p_h:
\[p\,=\,p_a\,+\,p_h\tag{1}\]
Atmostpheric pressure is caused by the gravitation of air column above the surface of the dam, hydrostatic pressure caused by the gravitation of water column above the bottom of the dam.

The value of standard atmospheric pressure is defined as:
\[ p_a\,=\,101.325\,\mathrm{kPa}\,=\,101 325\,\mathrm{Pa}\,.\tag{2}\]
For our calculation, we get by with the approximative value of 100 000 Pa.

There is a formula for hydrostatic pressure:
\[p_h\,=\,h{\rho}g,\tag{3}\]
where h is the depth of the water, ρ the density of the liquid and g = 10 N/kg (number we have to multiply the mass with to get the gravitational force).

Maximal depth is the difference of two altitudes plus the height of the risen water level (2 meters):
\[h=\left(\left(h_{1}-h_2\right)\,+\,h_0\right)=\left(\left(354-275\right)+2\right)\,\mathrm{m}\,=\,81\,\mathrm{m}\,.\tag{4}\]
From formulas (1), (2), (3) and (4) we get:
\[ p=p_a+\left(\left(h_{1}-h_2\right)+h_0\right){\rho}g\,,\] \[ p=\left(100 000+\left(\left(354-275\right)+2\right){\cdot}1000{\cdot}10\right)\,\mathrm{Pa}=910 000\,\mathrm{Pa}\,,\] \[ p= 910 \,\mathrm{kPa}\,.\]
The pressure in the water near the heel of the dam was approximately 910 kPa.

Task b):

The situation is depicted in the following picture:

If the water level rises by the height h′, the volume of water in the dam will increase:

V = S·h′

We solve the task by cross-multiplication:

The water increase in one second is (4400-3100) m³, hence:

1 s... 1300 m³

x s... S·h′

With numbers:
\[ x=\frac{S{\cdot}h'{\cdot}1}{1300}\mathrm{s}=\left(\frac{27\,300\,000{\cdot}1{\cdot}1}{1300}\right)\,\mathrm{s}=21\,000\,\mathrm{s}\,\dot=5.8\,\mathrm{h}\,. \]
The water level would rise 1 meter in approximetly 5.8 hours based on the given inflow and outflow.
Answer
a) \(p\,=\,p_a\,+\,((h_{1}\,-\,h_2)\,+\,h_0){\rho}g = 910 \,\mathrm{kPa}\)

The pressure in the water near the heel of the dam was approximately 910 kPa.

b) \(x\,=\,\frac{S{\cdot}h'{\cdot}1}{1300}\,\mathrm{s}\,\dot=\,5.8\,\mathrm{h}\)

The water level would rise 1 m in approximately 5.8 hours based on the given inflow and outflow.