Collection of Solved Problems in Physics

Wheel Rotation

Task number: 1998

• Given values

  f = 25 Hz	wheel rotation frequency
  t0 = 30 s	time after which the wheel stops
  ε = ? (s-2)	wheel angular acceleration
  N = ?	number of turns the wheel makes from the beginning of braking till stopping

• Hint 1 – Angular acceleration of the wheel

  What is the relation between the instantaneous value of angular velocity and angular acceleration of the wheel?

  What was the initial angular velocity the wheel had before it started decelerating? What was the angular speed at time t₀ ?

• Solution of Hint 1 – Angular acceleration of the wheel

  There is a formula for the instantaneous angular speed:

   

  \[\omega\,=\,\omega_0+\varepsilon{t}\,,\] \[\omega_0\,=\,2\pi f\,=\,50\pi\,\mathrm{s^{-1}}\,.\]

   

  At time    t = t₀ there will be ω = 0, so:

   

  \[\omega_0+\varepsilon{t_0}\,=\,0\,,\] \[\varepsilon\,=\,-\frac{\omega_0}{t_0}\,=\, -\frac{2\pi f}{t_0}\,=\,-\frac{50}{30}\pi\,\mathrm{s^{-2}}\,=\,-5.24\,\mathrm{s^{-2}}\,.\]

• Hint 2 – Number of revolutions - numerical solution

  How do you find out how many turns the wheel has made in a given time?

  Use the angle which the position vector sweeps out around the center of the wheel in the given time. Express it using the magnitude of angular acceleration that you know from the previous hint and the angular speed before braking.

• Solution of Hint 2 – Number of revolutions - numerical solution

  Position vector sweeps out with respect to the centre in time t₀ an angle:

   

  \[\psi_0\,=\,\omega_0t_0+\frac{\varepsilon{t_0^{2}}}{2}\,=\, 2{\pi}ft_0 + \frac{\varepsilon{t_0^{2}}}{2}\,,\] \[\psi_0\,=\, 1500\pi-\frac{5}{6}\pi900\,=\,750\pi\,.\]

   

  Number of turns in time t₀:

   

  \[N\,=\,\frac{\psi_0}{2\pi}\,=\,\frac{750\pi}{2\pi}\,=\,375\,.\]

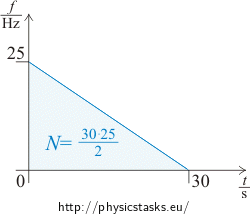
• Hint 3 – Number of turns - graphical solution

  Number of revolutions can be found graphically as well.

  Draw a graph of the rotating wheel frequency dependence on time. Where in the graph is the number of turns hidden?

• Solution of Hint 3 – Number of turns - graphical solution

  Graphical solution:

  

  Number of revolutions corresponds to the area under the curve.

• Complete Solution

  There is a formula for the instantaneous angular speed:

   

  \[\omega\,=\,\omega_0+\varepsilon t\,,\] \[\omega_0\,=\,2\pi f\,=\,50\pi\,\mathrm{s^{-1}}\,.\]

   

  At time t = t₀ there will be ω = 0, so:

   

  \[\omega_0+\varepsilon{t_0}\,=\,0\,,\] \[\varepsilon\,=\,-\frac{\omega_0}{t_0}\,=\,-\frac{2{\pi}f}{t_0} \,=\, -\frac{50}{30}\pi\,\mathrm{s^{-2}}\,=\,-5.24\,\mathrm{s^{-2}}\,.\]

   

  Position vector sweeps out with respect to the centre in time t₀ an angle:

   

  \[\psi_0\,=\,\omega_0t_0+\frac{\varepsilon{t_0^{2}}}{2}\,=\, 2{\pi}ft_0 + \frac{\varepsilon{t_0^{2}}}{2}\,,\] \[\psi_0\,=\, 1500\pi-\frac{5}{6}\pi900\,=\,750\pi\,.\]

   

  Number of revolutions in time t₀:

   

  \[N\,=\,\frac{\psi_0}{2\pi}\,=\,\frac{750\pi}{2\pi}\,=\,375\,.\]

   

  Graphical solution:

   

  

   

  Number of turns corresponds to the area under the curve.

• Answer

  Angular acceleration of the wheel ε is:

   

  \[\varepsilon\,=\,-\frac{2{\pi}f}{t_0} \,=\, -5.24\,\mathrm{s^{-2}}\,.\]

   

  Number of turns N that the wheel makes from the beginning of braking is:

   

  \[N\,=\,\frac{\psi_0}{2\pi}\,=\,ft_0 + \frac{\varepsilon{t_0^{2}}}{4\pi}\,=\,375\,.\]

• Number of turns – one more approach

  Number of revolutions the wheel makes can be found using the following method as well. Frequency changes with time according to equation:

  \[f\left(t\right)\,=\, f_0 - kt\,,\]

  where

  \[k\,=\,\frac{25}{30}\,.\]

  (slope of the line from graph 3 in Hint 3)

  Number of turns the wheel makes from the beginning of braking till stopping can be calculated as an integral of function f(t) in the particular time interval (area under the curve):

  \[N\,=\,\int_{0}^{30}{f(t)}\mathrm{d}t\,=\, \int_{0}^{30}{(f_0 - \frac{25}{30}t)}\mathrm{d}t\,,\] \[N\,=\,\int_{0}^{30}{(f_0 - \frac{5}{6}t)}\mathrm{d}t\,=\, \left[f_0t - \frac{5t^{2}}{6{\cdot}2}\right]_0^{30}\,,\] \[N\,=\, 25{\cdot}30 - \frac{5{\cdot}30^{2}}{2{\cdot}6} \,=\, 375\,.\]