Figure Skaters
Task number: 379
A figure skating couple consists of a man of mass m1 and a woman of mass m2. They are both skating together, the man closely behind the woman. They begin at rest. At one moment the man pushes upon the woman’s back and is applying a force F on her back for a time period Δt. Neither partner resists the motion. Neglect friction.
a) Find the figure skaters’ relative velocity v immediately after the push.
b) Find the work W done by both partners during pushing.
c) Now partners change they roles. This means that the woman skates behind the man and is appling the same force for the same time interval. How does this commutation change previous results a), b)?
d) Conceive of the previous situation (man behind woman) and assume that the man’s back is leaned against the wall. How does this situation change previous results a), b)?
First solve generally (algebraically) then for numerical values: m1 = 75 kg, m2 = 50 kg, F = 120 N,
Δt = 0.50 s.Hint a - the relative velocity of figure skaters
Draw a picture. Find the velocity of each partner immediately after the push. Use the relationship between the impulse and the change in linear momentum.
Hint b - the work
The work done equals the increase in the kinetic energy of the figure skaters due to the push. Find the energy and express it generally.
Hint c - changed roles
Make allowance for Newton’s third law (law of reciprocal actions).
Hint d - the barrier
Draw a picture. How will a momentum of the man change if he leans on the barrier?
Numerical solution
It is given:
\[m_1=75 \,\mathrm {kg}\] \[m_2=50 \,\mathrm {kg}\] \[F=120 \,\mathrm {N}\] \[\Delta t=0.50 \,\mathrm {s}\]a) We are looking for:
\[v=?\] \[v=\frac{m_1+m_2}{m_1m_2}F\Delta t\] \[v=\frac{75+50}{75{\cdot}50}120{\cdot}0{,}5\,\mathrm{ms^{-1}}\] \[v=2\,\mathrm{ms^{-1}}\]b) We are looking for:
\[W=?\] \[W=\frac{m_1+m_2}{2m_1m_2}F^2(\Delta t)^2\] \[W=\frac{75+50}{2{\cdot}75\cdot50}120^2{\cdot}0.5^2\,\mathrm{J}\] \[W=60\,\mathrm{J}\]c) Results of tasks a), b) do not change.
d) We are looking for:
\[v'=?\] \[W'=?\] \[v'=\frac{F\Delta t}{m_2}\] \[v'=\frac{120{\cdot}0.5}{75}\mathrm{ms^{-1}}\] \[v'=1{,}2\,\mathrm{ms^{-1}}\] \[W'=\frac{F^2(\Delta t)^2}{2m_2}\] \[W'=\frac{120^2{\cdot}0.5^2}{2{\cdot}75}\mathrm{J}\] \[W'=36\,\mathrm{J}\]Answer
a) The magnitude of figure skater’s relative velocity is \(v=\frac{m_1+m_2}{m_1m_2}F\Delta t=2\,\mathrm{ms^{-1}}\).
b) The work done by both of partners during push-off is \(W=\frac{m_1+m_2}{2m_1m_2}F^2(\Delta t)^2=60\,\mathrm{J}\).
c) Results of tasks a), b) do not change.
d) If the man leans on the barrier, figure skater’s relative velocity will be \(v'=\frac{F\Delta t}{m_2}=1{,}2\,\mathrm{ms^{-1}}\).
The work done in this case is \(W'=\frac{F^2(\Delta t)^2}{2m_2}=36\,\mathrm{J}\).
Complete solution of point a) - the relative velocity of figure skaters
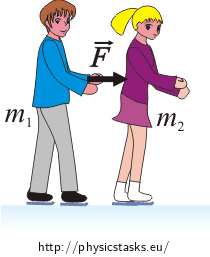
\(m_1\) ... the mass of the man
\(m_2\) ... the mass of the woman
The impulse equals the change in linear momentum per unit time. The force is in our case constant and acts in the direction of the motion of the partners so that the equation could be rewritten as:
\[F\Delta t=\Delta p\]For the woman we get:
\[F\Delta t= p_2-p_0\]\(F\) ... the force exerted on the woman by the man
\(p_2\) ... the momentum of the woman immediately after push-off
\(p_0\) ... the initial momentum of the woman (p0 = 0)
\[F\Delta t=m_2v_2\]\(v_2\) ... the velocity of the woman immediately after push-off
We express the velocity of the woman v2:
\[v_2=\frac{F\Delta t}{m_2}\tag{1}\]According to Newton’s third law (the law of reciprocal actions) the magnitude of the force exerted on the man by the woman equals the magnitude of the force F exerted on the woman by the man.
For the man we get:
\[F\Delta t= p_1-p'_0\]\(F\) ... the force exerted on the man by the woman
\(p_1\) ... the momentum of the man immediately after push-off
\(p'_0\) ... the initial momentum of he man (p'0 = 0)
\[F\Delta t=m_1v_1\]\(v_1\) ... the velocity of the man after push-off
We express the velocity of the man v1
\[v_1=\frac{F\Delta t}{m_1}\tag{2}\]The figure skaters’ relative velocity is always the vector difference \(\vec{v}_2 - \vec{v}_1\) of the two velocities. In this case, the velocities are in opposite directions so the numbers add:
\[v=v_1+v_2\]\(v\) ... the figure skaters’ relative velocity
Let’s insert v1, v2 from equations (1),(2). We get:
\[v=\frac{F\Delta t}{m_1}+\frac{F\Delta t}{m2}\] \[v=\frac{m_1+m_2}{m_1m_2}F\Delta t\] \[v=\frac{75+50}{75{\cdot}50}120{\cdot}0.5\,\mathrm{ms^{-1}}\] \[v=2\,\mathrm{ms^{-1}}\]Answer: The magnitude of figure skater’s relative velocity is \[v=\frac{m_1+m_2}{m_1m_2}F\Delta t = 2\,\mathrm{ms^{-1}}.\]
Complete solution of point b) - the work
During the pushing the kinetic energy of both figure skaters is increasing. The work done equals the total increase in the kinetic energies of both the man and the woman. (Neglect the change of internal energy.)
\[W=E_{k1}+E_{k2}\]\(W\) ... the work
\(E_{k1}\) ... the kinetic energy of the man
\(E_{k2}\) ... the kinetic energy of the woman
\[W=\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2\]Let’s insert v1 and v2 in equations (1) and (2):
\[W=\frac{1}{2}m_1\frac{F^2(\Delta t)^2}{m_1^2}+\frac{1}{2}m_2\frac{F^2(\Delta t)^2}{m_2^2}\] \[W=\frac{1}{2}F^2(\Delta t)^2\frac{(m_1+m_2)}{m_1m_2}\]Notice:
The done work could be determined using the Newton’s second law and the expression of the distance of the uniformly accelerated motion.
The women moves during pushing with constant accelaration:
\[a_2=\frac{F}{m_2}\tag{i}\]\(a_2\)..... the acceleration of the woman
She moves with uniform acceleration the distanes:
\[s_2=\frac{1}{2}a_2(\Delta t)^2\tag{ii}\]\(s_2\) ... the distance which the woman travels comapered with the man
Let’s insert a2 from the equation (i):
\[s_2=\frac{1}{2}\frac{F}{m_2}(\Delta t)^2\]The woman is during the pushing acting on the man with force F.
The man is moving with acceleration:
\[a_1=\frac{F}{m_1}\tag{iii}\]\(a_1\) ... the acceleration of the man
The man travels with uniform acceleration the distance:
\[s_1=\frac{1}{2}a_1(\Delta t)^2\tag{iv}\]\(s_1\) ... the distance which the man passes compared with the ice
Let’s insert acceleration a1 from equation (iii):
\[s_1=\frac{1}{2}\frac{F}{m_1}(\Delta t)^2\]The net work of the woman equals:
\[W=Fs_1+Fs_2\] \[W=F\frac{1}{2}\frac{F}{m_1}(\Delta t)^2+F\frac{1}{2}\frac{F}{m_2}(\Delta t)^2\] \[W=\frac{F^2}{2m_1}(\Delta t)^2+\frac{F^2}{2m_2}(\Delta t)^2\] \[W=\frac{m_1+m_2}{2m_1m_2}F^2(\Delta t)^2\]Answer: The work done by both of partners during push-off is \[W=\frac{m_1+m_2}{2m_1m_2}F^2(\Delta t)^2=60\,\mathrm{J}\] .
Complete solution of point c) - vyměněné role
Newton’s third law says that the forces of two bodies (in our case two figure skaters) on each other are always equal and are directed in opposite directions. Whenever the woman exerts a force F on the man, the man simultaneously exerts a force on the woman with the same magnitude in the opposite direction. The final effect is the same and the results of tasks a), b) do not change.
Answer: Results of tasks a), b) do not change.
Complete solution of point d) - the barrier
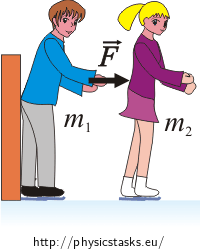
The man exerting a force F on the woman for a time interval Δt (at begining she was at rest) and gives her a momentum
\[p_2=F\Delta t,\]but he remains in place. The relative velocity equals the velocity of the woman.
\[m_2v_2=F\Delta t\] \[v_2= \frac{F\Delta t}{m_2}\] \[v'=v_2=\frac{F\Delta t}{m_2}\]The done work equals kinetic energy of the woman:
\[W'=\frac{1}{2}m_2v_2^2\] \[W'=\frac{1}{2}m_2\frac{F^2(\Delta t)^2}{m_2^2}=\frac{F^2(\Delta t)^2}{2m_2}\] \[W'=\frac{120^2{\cdot}0.5^2}{2{\cdot}75}\mathrm{J}\] \[W'=36\,\mathrm{J}\]Answer:
If the man leans on the barrier, figure skater’s relative velocity will be \(v'=\frac{F\Delta t}{m_2}=1.2\,\mathrm{ms^{-1}}\).
The work done in this case is \(W'=\frac{F^2(\Delta t)^2}{2m_2}=36\,\mathrm{J}\).


