Tricky Atwood Machine

Task number: 1751

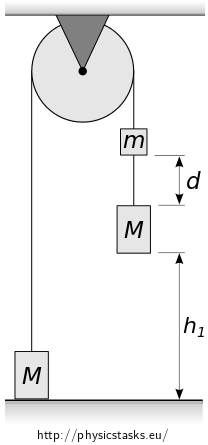
There are two weights of the same mass of \(2.0~\mathrm{kg}\) attached to a string looped over a braked pulley.

The left weight is lying on the floor, the right one is suspended \(1.0~\mathrm{m}\) above the floor.

There is another weight of mass \(0.5~\mathrm{kg}\) attached to the string \(20~\mathrm{cm}\) above the right weight.

The string except the part around the pulley is stretched vertically. We eventually release the pulley.

What is the speed at which the lower right weight hits the floor?
What is the height that the left weight rises to after the lower right weight falls inelastically to the floor?
What is the maximum height that the lower right weight rises back to?

Neglect the mass of both the string and the pulley, deformation of the string by tension, and friction.

Solve each part of the assignment in general first, then find the particular solution.

Preparations before solving the assignment
To solve the assignment we will need
- Newton’s laws of motion
- The law of conservation of momentum
- The law of conservation of energy (not necessary – only if you want)
We can also make use of knowing the following:
- What forces act upon a body.
- How to write the equation of motion for the given body.
- How to introduce an appropriate coordinate system and transform vector equations to scalar equations.
- How to solve simple simultaneous equations.
Let’s remember some kinematic equations
- The displacement of a uniformly accelerated motion with zero initial speed \[s = \frac{1}{2}at^2\mathrm{.}\]
- The speed of a uniformly accelerated motion with zero initial speed \[v = at.\]
If you don’t have any experience with problems with pulleys and strings, try to solve the equally interesting assignment Fixed Pulley first.

Note: Vector quantities in the pictures of this assignment are written in bold letters.

Notation

\(M=2.0~\mathrm{kg}\)	Mass of the two bigger weights
\(m=0.5~\mathrm{kg}\)	Mass of the smaller weight
\(d=20~\mathrm{cm}\)	Distance between the two weights on the right-hand side
\(h_1=1.0~\mathrm{m}\)	The initial height at which the lower right weight is suspended

a) Hint 1 – The Acceleration of the System
Our task is to calculate the speed \(v_1\) at which the lower right weight hits the floor. If we knew the equation of motion of this weight, we could easily calculate the speed using the height \(h_1\) that we know.
- How does the system move after we release the pulley?
- Can you determine the acceleration of this motion?
For a better understanding, draw a picture with all the forces that act upon the weights. Write the equations of motion in their vector form. Introduce an appropriate \(y\) axis and rewrite the equations of motion in their scalar form. Find the acceleration of the system.
a) Hint 1 – Solution
What forces are acting upon the weights?

The forces acting upon the left weight of mass \(M\) are
- Force of gravity \(\vec{G_{\mathrm{M}}}\)
- Tension force of the string \(\vec{T_{1}}\)
The forces acting upon the right weight of mass \(M\) are
- Force of gravity \(\vec{G_{\mathrm{M}}}\)
- Tension force of the string \(\vec{T_{2}^\prime}\)
The forces acting upon the right weight of mass \(m\) are
- Force of gravity \(\vec{G_{\mathrm{m}}}\)
- Tension force of the string \(\vec{T_{1}^\prime}\)
- Tension force of the string \(\vec{T_{2}}\)
Equations of motion

All of the weights are moving with an acceleration of the same magnitude \(a_1\).
The left weight M: \[ \vec{G_{\mathrm{M}}} + \vec{T_{1}} = M\vec{a_1} \tag{1}\] The lower right weight M: \[ \vec{G_{\mathrm{M}}} + \vec{T_{2}^\prime} = M\vec{a_1} \tag{2}\] The upper right weight m: \[ \vec{G_{\mathrm{m}}} + \vec{T_{1}^\prime} + \vec{T_{2}} = m\vec{a_1} \tag{3}\]

Equations of motion in their scalar form
We will introduce an appropriate \(y\) axis in the direction of the expected acceleration.
We will rewrite equations (1), (2), and (3) in their scalar form:

\(T_{1} - G_{\mathrm{M}} = Ma_1 \qquad\)(4)

\(G_{\mathrm{M}} - T_{2}^\prime= Ma_1 \qquad\)(5)

\(G_{\mathrm{m}} + T_{2} - T_{1}^\prime= ma_1\qquad\)(6)

Action and reaction, tension forces

We will neglect the mass of the pulley in accordance to the assignment. The pulley therefore does not have any moment of inertia and it doesn’t affect the tension forces of the string. The left weight M acts upon the upper right weight m via the string and vice versa. Similarly, the weights m and M on the right-hand side act upon each other. According to Newton’s third law we can write for the magnitudes of the tension forces:

\(T_{1}^\prime = T_{1}, \qquad\)(7)

\(T_{2}^\prime = T_{2}. \qquad\)(8)

Solving the equations of motion

We will add up equations (4), (5), (6), (7), and (8).
\[G_\mathrm{m} = (2M+m)a_1\tag{9}\]
We can express the force of gravity \(G_m\).
\[G_{\mathrm{m}} = mg \tag{10}\]
We substitute the force of gravity from (10) to (9).
\[mg = (2M+m)a_1\tag{11}\]
We express the required acceleration \(a_1\) from (11).
\[a_1 = \frac{mg}{2M+m}\tag{12}\]
a) Hint 2 – Speed on Impact
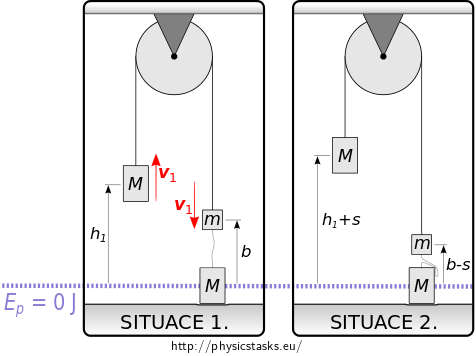
The analysis of the movement is shown in the picture. (1) shows the situation right before releasing the pulley, (2) shows the uniformly accelerated motion, and (3) is right when the lower right weight hits the floor.

Can you calculate the speed \(v_1\) of the lower right weight when it hits the floor falling from height \(h_1\), if you know that the motion is uniformly accelerated with acceleration \(a_1\) and that the initial speed of the weight is zero?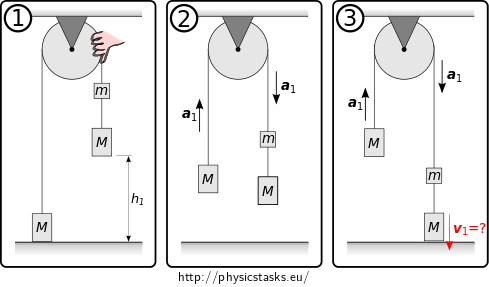
a) Hint 2 - Solution
The lower right weight is suspended at height \(h_1\) above the floor and is at rest with respect to the floor. After releasing the pulley the system starts moving with acceleration \(a_1\). The weight hits the floor after time \(t_1\).

The displacement over time \(t_1\) is:
\[h_1 = \frac{1}{2}a_1 t_1^2\tag{13}\]
The speed at time \(t_1\) is:
\[v_1 = a_1 t_1\tag{14}\] We can express the speed \(v_1\) by expressing \(t_1\) from equation (13) and substituting it in equation (14). We can then substitute \(a_1\) from equation (12). \[v_1 = \sqrt{2a_1 h_1} = \sqrt\frac{2mgh_1}{2M+m}\tag{15}\] We get the result for part a) by substituting the numerical values. \[v_1 = \sqrt\frac{2mgh_1}{2M+m} = \sqrt{\frac{2{\cdot} 0.5 {\cdot} 9.81 {\cdot} 1}{2{\cdot}2 + 0.5}}\mathrm{m\cdot s^{-1}} = 1.48~\mathrm{m\cdot s^{-1}}\]
a) Alternative Solution
An easier way to determine the speed of the lower right weight upon impact is to use the law of conservation of energy.

Let’s have a look at the following states of the system:

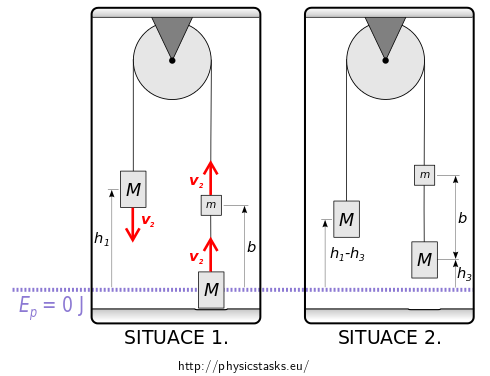
The first situation in which we will determine the total mechanical energy of the system is the moment right before realasing the pulley. (SITUATION 1.)

The second situation, which is the latest situation for which the total energy of the system is still conserved in the form of mechanical energy, is the moment right before the lower right weight hits the floor. (SITUATION 2.)

Law of conservation of mechanical energy:
The energy of the pulley and the string is zero, because we are neglecting their masses. \[ \begin{eqnarray*} E_{\mathrm{situation~1}} & =& E_{\mathrm{situation~2}} \\ Mgh_1 + mg(h_1+c) & =& Mgh_1 + mgc + \frac{1}{2} M v_1^2 + \frac{1}{2} M v_1^2 + \frac{1}{2} m v_1^2\\ mgh_1 &= & \frac{1}{2}(2M+m)v_1^2 \tag{16} \end{eqnarray*} \] We can calculate the speed \(v_1\) from equation (16). \[ v_1 = \sqrt\frac{2mgh_1}{2M+m} \]
b) Hint 1 – The Acceleration of the System
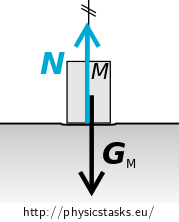
Consider the situation right after the lower right weight hits the floor (see the picture).
- What is the speed of each of the weights right after the lower right weight hits the floor?
- What happens to the string that connects the two weights on the right-hand side?
- Does the acceleration of the system change? How?
- What kind of motion will follow?
Determine the magnitude and the direction of acceleration \(a_2\) of the system after the lower right weight hits the floor.
b) Hint 1 - Solution
What is the situation after the weight hits the floor?

Right after the lower right weight hits the floor the system will try to stay in motion at the speed \(v_1\) which we have calculated in part a) of this assignment.

The string connecting the two weights on the right-hand side is no longer being stretched. The force of gravity \(\vec{G_M}\) acting upon the weight on the floor is compensated by the reaction of the floor \(\vec N\) and so the weight stays at rest.

Since the string connecting the two weights on the right is no longer stretched, the force \(\vec{T_2}\) no longer acts upon the weight of mass \(m\). The equations of motion of the system change and so does the acceleration of the system.

Looking at the distribution of the masses we can see that the new acceleration \(a_2\) will have a direction opposite to that of speed \(v_1\), we can therefore expect a uniformly decelerated motion with initial speed of \(v_1\).

The weights decelerate in the direction of the original motion until they come to a full stop and then start moving in the other direction with acceleration \(a_2\).

What forces are acting upon the weights?

The forces acting upon the left weight of mass \(M\) are
- Force of gravity \(\vec{G_{\mathrm{M}}}\)
- Tension force of the string \(\vec{T_{3}}\)
The forces acting upon the right weight of mass \(m\) are
- Force of gravity \(\vec{G_{\mathrm{m}}}\)
- Tension force of the string \(\vec{T_{3}^\prime}\)
Equations of motion

Both weights are moving with the acceleration \(a_2\).
The left weight of mass M: \[ \vec{G_{\mathrm{M}}} + \vec{T_{3}} = M\vec{a_2} \tag{17}\] The right weight of mass m: \[ \vec{G_{\mathrm{m}}} + \vec{T_{3}^\prime} = m\vec{a_2} \tag{18}\]

Equations of motion in scalar form
We will introduce an appropriate \(y\) axis in the direction of the expected acceleration.
We will rewrite equations (17) and (18) in their scalar form:

\(G_{\mathrm{M}} - T_{3} = Ma_2 \qquad\)(19)

\(T_{3}^\prime - G_{\mathrm{m}} = ma_2\qquad\)(20)

Action and reaction, tension forces

We will neglect the mass of the pulley in accordance to the assignment. The pulley therefore does not have any moment of inertia and it doesn’t affect the tension forces of the string. The left weight M acts upon the upper right weight m via the string and vice versa. According to Newton’s third law we can write for the magnitudes of the tension forces:

\(T_{3} = T_{3}^\prime. \qquad\)(21)

Solving the equations of motion

By adding up equations (19), (20), and (21) we get
\[G_M - G_m = a_2(M+m). \] We express the acceleration \(a_2\) and substitute the tension forces. \[ a_2 = \frac{G_M - G_m}{M+m} = g\frac{M-m}{M+m} \tag{22}\]
b) Hint 2 – Height of Rise of the Weight
We found that the reduced system of the left weight of mass \(M\) and the upper right weight of mass \(m\) is going to move in a uniformly decelerated motion with deceleration \(a_2\). The initial speed of the motion is \(v_1\).

Can you calculate the displacement \(s\) of the weight in this motion until it comes to a complete stop? What is the height \(h_2\) of the left weight above the floor?

Discuss the case for \(s\gt d\).
b) Hint 2 - Solution
The system is in a uniformly decelerated motion with deceleration \(a_2\) until it stops. If the motion takes time \(t_2\) then the initial speed and the displacement of the motion can be expressed as:
\[ v_1 = a_2 t_2, \tag{23}\] \[ s = \frac12 a_2 t_2^2. \tag{24}\] We substitute time \(t_2\) from equation (23) to equation (24). Then we can substitute the acceleration \(a_2\)we calculated in equation (22) and the speed \(v_1\) from (15). \[ s = \frac12 \frac{v_1^2}{a_2} = \frac{h_1 m(M+m)}{(2M+m)(M-m)} \] We substitute the numerical values. \[ s = \frac{h_1 m(M+m)}{(2M+m)(M-m)} = \frac{1\cdot\, 0.5\cdot(2+0.5)}{(2{\cdot} 2 + 0.5)(2-0.5)}~\mathrm{m} = 0.185~\mathrm{m} \]
- The system will try to cover the displacement \(s=0.185~\mathrm{m}\).
- The distance between the two weights on the right-hand side is \(d = 20~\mathrm{cm}\).
Since \(s\lt d,\) the upper right weight will stop above the lower weight.
The left weight will rise by \(s\) it will therefore be at height
\[h_2 = h_1 + s = (1 + 0.185)~\mathrm{m}=1.185~\mathrm{m}.\]
In case that \(s\gt d\) the system would get further reduced to just the left weight of mass \(M\) which would then move in a uniformly decelerated motion with deceleration \(g\). The next displacement upwards could be calculated in a similar manner.
b) Alternative Solution
The height \(h_2\), to which the left weight rises after the lower right weight falls inelastically to the floor, can be determined faster using the law of conservation of mechanical energy.

After the lower right weight inelastically falls to the floor, the mechanical energy of the system gets reduced by the kinetic energy of the weight right before it hits the floor. This mechanical energy is converted to the internal energy of the fallen weight and the floor.

After the collision the mechanical energy is lower but it gets conserved until the next collision.

Let’s look at the following systems:

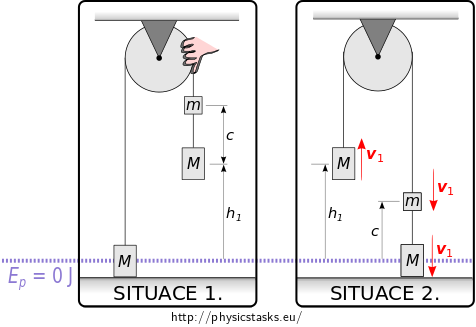
The first situation shows the moment right after the perfectly inelastic collision of the lower left weight and the floor. The other weights are moving with speed \(v_1\) calculated in part a) of this assignment.(SITUATION 1.)

The second situation in which we will look at the total mechanical energy of the system is the moment when the speed of both of the weights suspended over the pulley is zero. At this moment the left weight is at a maximum height above the floor, i.e. the desired height \(h_2\). (SITUATION 2.)

Law of conservation of mechanical energy:
The energy of the pulley and the string is zero, because we are neglecting their masses. \[ \begin{eqnarray*} E_{\mathrm{situace~1}} & =& E_{\mathrm{situace~2}} \\ Mgh_1 + mgb + \frac12 M v_1^2 + \frac12 m v_1^2 & =& Mg(h_1 + s) + mg(b-s)\\ \frac12 (M+m) v_1^2 &= & (M-m)gs \tag{25} \end{eqnarray*} \] We can express the displacement \(s\) of the system form equation (25). We substitute for \(v_1\) from equation (15). \[ s = \frac{v_1^2(M+m)}{2g(M-m)} = \frac{h_1 m(M+m)}{(2M+m)(M-m)}. \] We substitute the numerical values. \[ s = \frac{h_1 m(M+m)}{(2M+m)(M-m)} = \frac{1\cdot\, 0.5\cdot(2+0.5)}{(2{\cdot} 2 + 0.5)(2-0.5)}~\mathrm{m} = 0.185~\mathrm{m} \]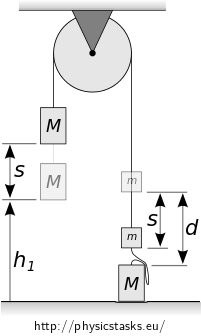
- For the energy \(E_k\) of the system to be zero, the upper right weight of mass \(m\) has to descend by \(s=0.185~\mathrm{m}\).
- The initial distance between the two weights on the right is \(d = 20~\mathrm{cm}\).
Since \(s\lt d,\) the upper right weight stops above the lower right weight.
The left weight rises by \(s\), it will therefore be at height
\[h_2 = h_1 + s = (1 + 0.185)~\mathrm{m}=1.185~\mathrm{m}.\]
In case that \(s\gt d\) the system would get further reduced to just the left weight of mass \(M\) which would then move in a uniformly decelerated motion with deceleration \(g\). The next displacement upwards could be calculated in a similar manner.
c) Hint 1 - Jolt upon Stretching the String
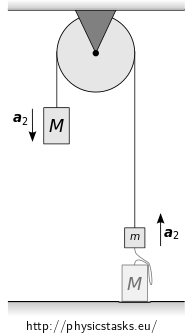
The system of the weight and the pulley as we left it in part b) of this assignment is shown in the picture on the right.

Keep in mind that the system hasn’t changed and that the acceleration of the system is still the same.
- How will the system move from this point onward?
- What will happen when the loose string gets stretched again?
- At what speed does the system move right before it stretches the string?
- How will the speed of the system change when it stretches the string, that is, when the weight on the floor starts moving?
- What acceleration will the system have after the string stretches? Don’t we know it already?
Calculate the speed \(v_2\) with which the system will move after the string stretches, that is after the weight on the floor starts moving.
c) Hint 1 – Solution
The string connecting the two weights on the right is still loose. The equations of motion we considered in part b) are still valid and the system still moves in a uniformly accelerated motion with acceleration \(a_2\) but pointing in the other direction.

The system keeps accelerating until the upper right weight of mass \(m\) reaches height \(d\) above the lower right weight.

This is an inverse motion to the motion in part b). The system right before the string stretches will move at the known speed \(v_1\).

By stretching the string connecting the two weights on the right, the lower right weight starts moving. The mass of the system grows to \(2M+m\) and the speed changes suddenly to \(v_2\). We can understand this phenomenon as an analogy to a perfectly inelastic collision.

The system during the jolt is isolated and the law of conservation of momentum applies:
\[\sum_i^N \vec{p_i} = \overset{\longrightarrow}{konst}.\]

The total momentum of the system before and after the collision are equal to each other. \[ \begin{eqnarray} \vec{p_\mathrm{pred}} &= & \vec{p_\mathrm{po}}\\ M\vec{v_1} + m\vec{v_1} &= & M\vec{v_2} + m\vec{v_2} + M\vec{v_2} \end{eqnarray} \] If we introduce a \(y\) axis as shown in the picture, the law of conservation of momentum can be rewritten in scalar form. \[ \begin{eqnarray} Mv_1 + mv_1 &= & Mv_2 + mv_2 + Mv_2 \\ v_1(M+m) &= & v_2(2M + m)\\ \end{eqnarray} \] We can express the desired speed \(v_2\). We substitute for \(v_1\) from equation (15). \[ v_2 = \frac{M+m}{2M+m}v_1 = \frac{M+m}{2M+m}\sqrt{\frac{2mgh_1}{2M+m}} \tag{26}\]
By stretching the string the lower right weight, which until now was standing still on the floor, becomes part of the system as it was in the beginning. The system now follows the equations of motion calculated in part a) of this assignment. A uniformly decelerated motion with initial speed \(v_2\) and acceleration \(a_1\) from equation (12) will follow.
c) Hint 2 – Maximum height
Can you calculate the displacement of the system before it reaches zero speed, if it moves in a uniformly decelerated motion with acceleration \(a_1\) and initial speed \(v_2\)?

What is the maximum height \(h_3\) above the floor that the lower right weight reaches?
c) Hint 2 - Solution
The system will move in a uniformly decelerated motion with acceleration \(a_1\) until it stops. If it takes time \(t_3\), the initial speed and the displacement can be expressed as:
\[ v_2 = a_1 t_3, \tag{27}\] \[ h_3 = \frac12 a_1 t_3^2. \tag{28}\] We substitute time \(t_3\) from equation (27) to equation (28). Then we substitute the known acceleration \(a_1\) from equation (12) and speed \(v_2\) from equation (26). \[ h_3 = \frac12 \frac{v_2^2}{a_1} = h_1\left(\frac{M+m}{2M+m}\right)^2 \] By substituting the numerical values we get the desired height \(h_3\) that the lower right weight reaches above the floor. \[ h_3 = h_1\left(\frac{M+m}{2M+m}\right)^2 = 1\cdot\left(\frac{2+0.5}{2{\cdot} 2 + 0.5}\right)^2~\mathrm{m} = 0.31~\mathrm{m} \]
c) Hint 2 – Alternative Solution
The maximum height \(h_3\) that the lower right weight reaches after the string stretches can be determined more easily by using the law of conservation of mechanical energy.

Let’s have a look at the following systems:

(SITUATION 1.) - The first situation shows the moment right before the string stretches. Since the lower right weight starts moving, the speed of the system drops to \(v_2\), which we have calculated in part c) Hint 1 – Solution.

(SITUATION 2.) - The second situation, in which we will look at the total mechanical energy of the system, is the moment when the lower right weight reaches the maximum height. The speed of the weight is zero.

Law of conservation of mechanical energy:
The energy of the pulley and the string is zero because we neglect their masses. \[ \begin{eqnarray*} Mgh_1 + mgb + \frac12 (2M+m) v_2^2 &= & Mg(h_1-h_3) + Mgh_3 + mg(b+h_3)\\ \frac12 (2M+m)v_2^2 &= & mgh_3 \tag{29} \end{eqnarray*} \] We calculate the desired maximum height \(h_3\) from equation (29). We substitute \(v_2\) from equation (26). \[ h_3 = \frac{v_2^2(2M+m)}{2mg} = h_1\left(\frac{M+m}{2M+m}\right)^2 \] We substitute the numerical values: \[ h_3 = h_1\left(\frac{M+m}{2M+m}\right)^2 = 1\cdot\left(\frac{2+0{.}5}{2{\cdot} 2 + 0{.}5}\right)^2~\mathrm{m} = 0{.}31~\mathrm{m} \]
COMPLETE SOLUTION
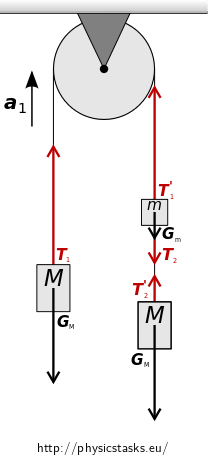
What forces are acting upon the weights?

The forces acting upon the left weight of mass \(M\) are
- Force of gravity \(\vec{G_{\mathrm{M}}}\)
- Tension force of the string \(\vec{T_{1}}\)
The forces acting upon the right weight of mass \(M\) are
- Force of gravity \(\vec{G_{\mathrm{M}}}\)
- Tension force of the string \(\vec{T_{2}^\prime}\)
The forces acting upon the right weight of mass \(m\) are
- Force of gravity \(\vec{G_{\mathrm{m}}}\)
- Tension force of the string \(\vec{T_{1}^\prime}\)
- Tension force of the string \(\vec{T_{2}}\)
Equations of motion

All of the weights are moving with an acceleration of the same magnitude \(a_1\).
The left weight M: \[ \vec{G_{\mathrm{M}}} + \vec{T_{1}} = M\vec{a_1} \tag{1}\] The lower right weight M: \[ \vec{G_{\mathrm{M}}} + \vec{T_{2}^\prime} = M\vec{a_1} \tag{2}\] The upper right weight m: \[ \vec{G_{\mathrm{m}}} + \vec{T_{1}^\prime} + \vec{T_{2}} = m\vec{a_1} \tag{3}\]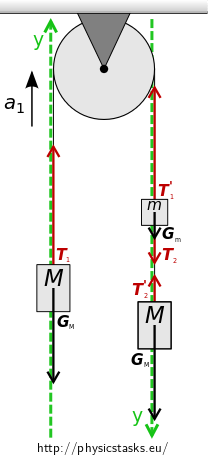

Equations of motion in their scalar form
We will introduce an appropriate \(y\) axis in the direction of the expected acceleration.
We will rewrite equations (1), (2), and (3) in their scalar form:

\(T_{1} - G_{\mathrm{M}} = Ma_1 \qquad\)(4)

\(G_{\mathrm{M}} - T_{2}^\prime= Ma_1 \qquad\)(5)

\(G_{\mathrm{m}} + T_{2} - T_{1}^\prime= ma_1\qquad\)(6)

Action and reaction, tension forces

We will neglect the mass of the pulley in accordance to the assignment. The pulley therefore does not have any moment of inertia and it doesn’t affect the tension forces of the string. The left weight M acts upon the upper right weight m via the string and vice versa. Similarly, the weights m and M on the right-hand side act upon each other. According to Newton’s third law we can write for the magnitudes of the tension forces:

\(T_{1}^\prime = T_{1}, \qquad\)(7)

\(T_{2}^\prime = T_{2}. \qquad\)(8)

Solving the equations of motion

We will add up equations (4), (5), (6), (7), and (8).
\[G_\mathrm{m} = (2M+m)a_1\tag{9}\]
We can express the force of gravity \(G_m\).
\[G_{\mathrm{m}} = mg \tag{10}\]
We substitute the force of gravity from (10) to (9).
\[mg = (2M+m)a_1\tag{11}\]
We express the required acceleration \(a_1\) from (11).
\[a_1 = \frac{mg}{2M+m}\tag{12}\]
The lower right weight is suspended at height \(h_1\) above the floor and is at rest with respect to the floor. After releasing the pulley the system starts moving with acceleration \(a_1\). The weight hits the floor after time \(t_1\).

The displacement over time \(t_1\) is:
\[h_1 = \frac{1}{2}a_1 t_1^2\tag{13}\]
The speed at time \(t_1\) is:
\[v_1 = a_1 t_1\tag{14}\] We can express the speed \(v_1\) by expressing \(t_1\) from equation (13) and substituting it in equation (14). We can then substitute \(a_1\) from equation (12). \[v_1 = \sqrt{2a_1 h_1} = \sqrt\frac{2mgh_1}{2M+m}\tag{15}\] We get the result for part a) by substituting the numerical values. \[v_1 = \sqrt\frac{2mgh_1}{2M+m} = \sqrt{\frac{2{\cdot} 0.5 {\cdot} 9.81 {\cdot} 1}{2{\cdot}2 + 0.5}}\mathrm{m\cdot s^{-1}} = 1.48~\mathrm{m\cdot s^{-1}}\]

What is the situation after the weight hits the floor?

Right after the lower right weight hits the floor the system will try to stay in motion at the speed \(v_1\) which we have calculated in part a) of this assignment.

The string connecting the two weights on the right-hand side is no longer being stretched. The force of gravity \(\vec{G_M}\) acting upon the weight on the floor is compensated by the reaction of the floor \(\vec N\) and so the weight stays at rest.

Since the string connecting the two weights on the right is no longer stretched, the force \(\vec{T_2}\) no longer acts upon the weight of mass \(m\). The equations of motion of the system change and so does the acceleration of the system.

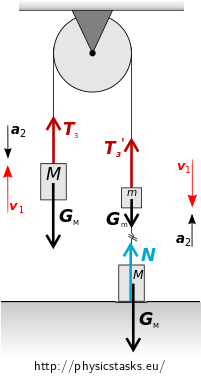
Looking at the distribution of the masses we can see that the new acceleration \(a_2\) will have a direction opposite to that of speed \(v_1\), we can therefore expect a uniformly decelerated motion with initial speed of \(v_1\).

The weights decelerate in the direction of the original motion until they come to a full stop and then start moving in the other direction with acceleration \(a_2\).

What forces are acting upon the weights?

The forces acting upon the left weight of mass \(M\) are
- Force of gravity \(\vec{G_{\mathrm{M}}}\)
- Tension force of the string \(\vec{T_{3}}\)
The forces acting upon the right weight of mass \(m\) are
- Force of gravity \(\vec{G_{\mathrm{m}}}\)
- Tension force of the string \(\vec{T_{3}^\prime}\)
Equations of motion

Both weights are moving with the acceleration \(a_2\).
The left weight of mass M: \[ \vec{G_{\mathrm{M}}} + \vec{T_{3}} = M\vec{a_2} \tag{17}\] The right weight of mass m: \[ \vec{G_{\mathrm{m}}} + \vec{T_{3}^\prime} = m\vec{a_2} \tag{18}\]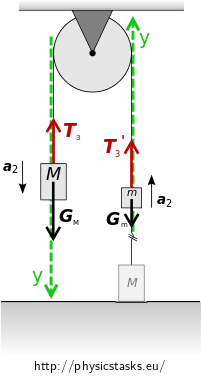

Equations of motion in scalar form
We will introduce an appropriate \(y\) axis in the direction of the expected acceleration.
We will rewrite equations (17) and (18) in their scalar form:

\(G_{\mathrm{M}} - T_{3} = Ma_2 \qquad\)(19)

\(T_{3}^\prime - G_{\mathrm{m}} = ma_2\qquad\)(20)

Action and reaction, tension forces

We will neglect the mass of the pulley in accordance to the assignment. The pulley therefore does not have any moment of inertia and it doesn’t affect the tension forces of the string. The left weight M acts upon the upper right weight m via the string and vice versa. According to Newton’s third law we can write for the magnitudes of the tension forces:

\(T_{3} = T_{3}^\prime. \qquad\)(21)

Solving the equations of motion

By adding up equations (19), (20), and (21) we get
\[G_M - G_m = a_2(M+m). \] We express the acceleration \(a_2\) and substitute the tension forces. \[ a_2 = \frac{G_M - G_m}{M+m} = g\frac{M-m}{M+m} \tag{22}\]
The system is in a uniformly decelerated motion with deceleration \(a_2\) until it stops. If the motion takes time \(t_2\) then the initial speed and the displacement of the motion can be expressed as:
\[ v_1 = a_2 t_2, \tag{23}\] \[ s = \frac12 a_2 t_2^2. \tag{24}\] We substitute time \(t_2\) from equation (23) to equation (24). Then we can substitute the acceleration \(a_2\)we calculated in equation (22) and the speed \(v_1\) from (15). \[ s = \frac12 \frac{v_1^2}{a_2} = \frac{h_1 m(M+m)}{(2M+m)(M-m)} \] We substitute the numerical values. \[ s = \frac{h_1 m(M+m)}{(2M+m)(M-m)} = \frac{1\cdot\, 0.5\cdot(2+0.5)}{(2{\cdot} 2 + 0.5)(2-0.5)}~\mathrm{m} = 0.185~\mathrm{m} \]
- The system will try to cover the displacement \(s=0.185~\mathrm{m}\).
- The distance between the two weights on the right-hand side is \(d = 20~\mathrm{cm}\).
Since \(s\lt d,\) the upper right weight will stop above the lower weight.
The left weight will rise by \(s\) it will therefore be at height
\[h_2 = h_1 + s = (1 + 0.185)~\mathrm{m}=1.185~\mathrm{m}.\]
In case that \(s\gt d\) the system would get further reduced to just the left weight of mass \(M\) which would then move in a uniformly decelerated motion with deceleration \(g\). The next displacement upwards could be calculated in a similar manner.

The string connecting the two weights on the right is still loose. The equations of motion we considered in part b) are still valid and the system still moves in a uniformly accelerated motion with acceleration \(a_2\) but pointing in the other direction.

The system keeps accelerating until the upper right weight of mass \(m\) reaches height \(d\) above the lower right weight.

This is an inverse motion to the motion in part b). The system right before the string stretches will move at the known speed \(v_1\).

By stretching the string connecting the two weights on the right, the lower right weight starts moving. The mass of the system grows to \(2M+m\) and the speed changes suddenly to \(v_2\). We can understand this phenomenon as an analogy to a perfectly inelastic collision.

The system during the jolt is isolated and the law of conservation of momentum applies:
\[\sum_i^N \vec{p_i} = \overset{\longrightarrow}{konst}.\]

The total momentum of the system before and after the collision are equal to each other. \[ \begin{eqnarray} \vec{p_\mathrm{pred}} &= & \vec{p_\mathrm{po}}\\ M\vec{v_1} + m\vec{v_1} &= & M\vec{v_2} + m\vec{v_2} + M\vec{v_2} \end{eqnarray} \] If we introduce a \(y\) axis as shown in the picture, the law of conservation of momentum can be rewritten in scalar form. \[ \begin{eqnarray} Mv_1 + mv_1 &= & Mv_2 + mv_2 + Mv_2 \\ v_1(M+m) &= & v_2(2M + m)\\ \end{eqnarray} \] We can express the desired speed \(v_2\). We substitute for \(v_1\) from equation (15). \[ v_2 = \frac{M+m}{2M+m}v_1 = \frac{M+m}{2M+m}\sqrt{\frac{2mgh_1}{2M+m}} \tag{26}\]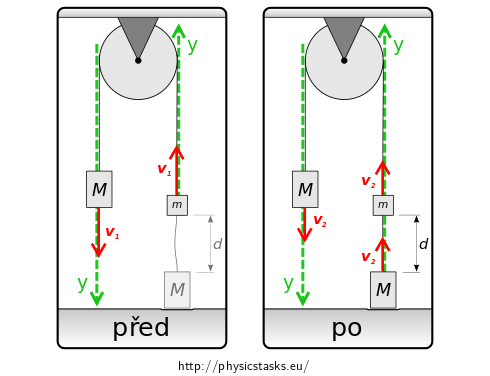
By stretching the string the lower right weight, which until now was standing still on the floor, becomes part of the system as it was in the beginning. The system now follows the equations of motion calculated in part a) of this assignment. A uniformly decelerated motion with initial speed \(v_2\) and acceleration \(a_1\) from equation (12) will follow.

The system will move in a uniformly decelerated motion with acceleration \(a_1\) until it stops. If it takes time \(t_3\), the initial speed and the displacement can be expressed as:
\[ v_2 = a_1 t_3, \tag{27}\] \[ h_3 = \frac12 a_1 t_3^2. \tag{28}\] We substitute time \(t_3\) from equation (27) to equation (28). Then we substitute the known acceleration \(a_1\) from equation (12) and speed \(v_2\) from equation (26). \[ h_3 = \frac12 \frac{v_2^2}{a_1} = h_1\left(\frac{M+m}{2M+m}\right)^2 \] By substituting the numerical values we get the desired height \(h_3\) that the lower right weight reaches above the floor. \[ h_3 = h_1\left(\frac{M+m}{2M+m}\right)^2 = 1\cdot\left(\frac{2+0.5}{2{\cdot} 2 + 0.5}\right)^2~\mathrm{m} = 0.31~\mathrm{m} \]
COMPLETE ANSWER
1. The lower right weight hits the floor at the speed \(v_1 = 1.48~\mathrm{m\cdot s^{-1}}\).
2. After the lower right weight inelastically falls to the floor, the left weight rises to the height \(h_2 = 1.185~\mathrm{m}\).
3. The maximum height that the lower right weight then reaches is \(h_3 = 0.31~\mathrm{m}\).