Movement of a Particle II
Task number: 1989
The position vector of a particle changes with time according to relation:
\[\vec{r}\left(t\right)\,=\,15\,\mathrm{m\,s^{-2}}t^2\vec{\,i\,}+\left(4\,\mathrm{m}-20\,\mathrm{m\,s^{-2}}t^2\right)\vec{\,j\,}\,,\]where \(\vec{\,i\,}\), \(\vec{\,j\,}\) are unit vectors in directions of coordinate axes x and y.
Solve the following tasks:
a) What is the trajectory of the particle? Write its equation.
b) Draw the trajectory of the particle.
c) Determine the distance it will travel in any given time interval (tk1, tk2).
d) Determine the distance the particle traveled on the section between the x axis and the y axis.
e) How long did it take the particle to travel in the section between the x axis and the y axis?
f) What is the average speed in the section between the x axis and the y axis? (speed refers to the magnitude of velocity).
g) Can the average speed of the particle be calculated using the formula \[v\,=\,\frac{v_1+v_2}{2},\] where v1is the initial speed and v2 is the final speed of the movement?
Justify your answer.
Note: Parametric equations should be writen in the following form:
\[y\,=\,1\,\mathrm{m} - 2\,\mathrm{m\,s^{-1}}\cdot t\,.\]We do not use units in relations to simplify the notation.
Hint 1 for a): Equation describing the trajectory of the particle
Which relations describe the movement of the particle in directions of the coordinate axes x, y, z?
(You can use the solved tasks from the problem Movement of a Particle I
How do you obtain the equation of the trajectory of the particle from the parametric equations x(t), y(t), z(t)?
Hint 2 for b): Trajectory of the particle
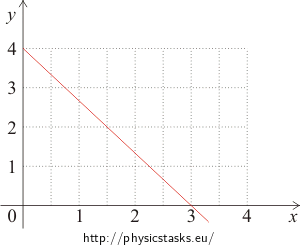
We need to draw a straight line described by the equation \(y\,=\,4-\left(\frac{4}{3}\right)x\). All we need is to find two points the line passes through. For example, find out at which points it crosses the x axis and the y axis.
Hint 3 for c): Distance travelled in a time interval (tk1, tk2)
You know from the problem Movement of a Particle I how the speed of the particle changes with time:
\[v\left(t\right)\,=\,50t\,.\]What is the relation between the distance travelled by the particle and its speed?
Determine the distance for the time interval (tk1; tk2).
Hint 4 for d): Distance travelled between the x and the y axis
You can use the solution from task c) (see Hint 3). You also need to know the times at which the particle crossed the x axis and the y axis. This task is solved in the problem Movement of a Particle I.
You can also use the picture showing the trajectory of the particle to determine the distance.
Hint 5 for e): Duration of the journey travelled between the x and the y axis
Realize that you know the times when the particle crosses the x and y axis.
Hint 6 for f): Average speed between the x and the y axis
What is the definition of average speed?
Do you know all the quantities needed for the calculation?
Hint 7 for g): Calculation of the average speed of the particle
Try to express the average speed of the particle as the arithmetic mean of the initial speed v1 and the final speed v2 when velocity is linearly dependent on time.
Can this formula be used for any function of speed v(t)?
Overall solution
Note: We do not use units in relations to simplify the notation.
We use solved tasks in the problem Movement of a Particle I:
a)
The movement of the particle in directions of the individual coordinate axes is described with relations:
\[x\left(t\right)\,=\,15t^{2}\,,\tag{1}\] \[y\left(t\right)\,=\,4-20t^{2}\,,\tag{2}\] \[z\left(t\right)\,=\,0\,.\tag{3}\]We obtain trajectory by excluding the parameter t from equations x(t), y(t), z(t).
From (1):
\[t^{2}\,=\,\frac{x}{15}\,.\]We substitute into (2):
\[y\,=\,4-\left(\frac{20}{15}\right)x\,=\,4-\left(\frac{4}{3}\right)x\,,\] \[x\,\geq\,0\,,\] \[z\,=\,0\,.\]b)
Point of intersection with the y axis: x = 0 y = 4.
Point of intersection with the x axis: y = 0 4 = 4x/3 x = 3.
The line passes through points with coordinates: [0;4] and [3;0].
Trajectory of the particle:
c)
We can calculate the distance travelled by the particle from its speed as:
\[s\,=\,\int{v\left(t\right)}\mathrm{d}t\,.\]It holds for the distance travelled in the time interval (tk1, tk2) that:
\[s\,=\,\int_\mathrm{t_{k1}}^{t_\mathrm{k2}}{v\left(t\right)}\,\mathrm{d}t\,=\,\int_\mathrm{t_{k1}}^{t_\mathrm{k2}}{50t}\,\mathrm{d}t\,=\,\left[25t^{2}\right]_{t_\mathrm{k1}}^{t_\mathrm{k2}}\,=\,25\left(t_\mathrm{k2}^{2}-t_\mathrm{k1}^{2}\right)\,.\]d)
We can use the solution from task c) (see Hint 3). We also need to know the times at which the particle crossed the x axis and the y axis.
\[s\,=\,\int_{t_1}^{t_2}{v\left(t\right)}\,\mathrm{d}t\,=\,\int_{t_1}^{t_2}{50t}\,\mathrm{d}t\,=\,\left[25t^{2}\right]_{t_1}^{t_2}\,=\,25\left(t_2^{2}-t_1^{2}\right)\,,\]where:
\(t_1\,=\,0\,\mathrm{s}\hspace{15px}\) is the time of crossing the y axis (see Movement of a Particle I)
\(t_2\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\hspace{15px}\) the time of crossing the x axis (see Movement of a Particle I)
\[s\,=\,25\cdot\left(\frac{1}{\sqrt{5}}\right)^{2}-25{\cdot} 0\] \[s\,=\,5\,\mathrm{m}\]We can also determine the distance from the picture showing the trajectory of the particle:
\[s\,=\,\sqrt{4^{2}+3^{2}}\,\mathrm{m}\,=\,5\,\mathrm{m}\,.\]e)
We determine the time needed to travel between the x axis and the y axis as:
\[\Delta{t}\,=\,t_2-t_1\,,\]Where:
\(t_1\,=\,0\,\mathrm{s}\hspace{15px}\)is the time of crossing the y axis
\(t_2\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\hspace{15px}\)is the time of crossing the x axis
Then it holds that:
\[\Delta{t}\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}-0\,\mathrm{s}\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\,.\]f)
The average speed of the particle between the x axis and the y axis is defined as the total distance travelled on this section divided by the total duration of the movement. We know the total distance travelled and the total duration of movement on this section from the solutions of tasks d) and e).
Therefore:
\[v\,=\,\frac{\Delta{s}}{\Delta{t}}\,=\,\frac{5}{\frac{1}{\sqrt{5}}}\,\mathrm{m\,s^{-1}}\,=\,5\sqrt{5}\,\mathrm{m\,s^{-1}}\,.\]g)
Average speed is given by the relation:
\[v_\mathrm{a}\,=\, \frac{\Delta{s}}{\Delta{t}}\,=\,\frac{ \int_\mathrm{t_\mathrm{1}}^{t_\mathrm{2}}{v(t)}\,\mathrm{d}t }{t_\mathrm{2}-t_\mathrm{1}}\,.\]If speed is a linear function of time \(v(t)\,=\,k\cdot t\), then it holds that:
\[v_\mathrm{a}\,=\,\frac{\int_\mathrm{t_\mathrm{1}}^{t_\mathrm{2}}{k.t}\,\mathrm{d}t}{t_\mathrm{2}-t_\mathrm{1}}\,=\,\frac{\frac{1}{2}kt_\mathrm{2}^{2}-\frac{1}{2}kt_\mathrm{1}^{2}}{t_\mathrm{2}-t_\mathrm{1}}\,=\,\frac{\frac{k}{2}\left(t_\mathrm{2}+t_\mathrm{1}\right)\left(t_\mathrm{2}-t_\mathrm{1}\right)}{t_\mathrm{2}-t_\mathrm{1}}\,,\] \[v_\mathrm{a}\,=\,\frac{k}{2}\left(t_\mathrm{2}+t_\mathrm{1}\right)\,=\,\frac{v_\mathrm{1}+v_\mathrm{2}}{2}\,.\]The stated formula holds for any function v(t) that is a linear function of time.
Therefore it can also be used in our scenario:
\[v_\mathrm{1}\,=\,50t_\mathrm{1}\,=\,50{\cdot} 0 \,\mathrm{m\,s^{-1}}\,=\, 0\,\mathrm{m\,s^{-1}}\,,\] \[v_\mathrm{2}\,=\,50t_\mathrm{2}\,=\,50\cdot \frac{1}{\sqrt{5}} \,\mathrm{m\,s^{-1}}\,=\,\frac{50}{\sqrt{5}}\,\mathrm{m\,s^{-1}}\,=\,10\sqrt{5}\,\mathrm{m\,s^{-1}}\,,\] \[v_\mathrm{a}\,=\,\frac{\left(v_\mathrm{1}+v_\mathrm{2}\right)}{2}\,=\,\frac{10\sqrt{5}}{2}\,=\,5\sqrt{5}\,\mathrm{m\,s^{-1}}\,.\]The stated formula cannot be generally used for functions v(t) which are not linear functions of time.
Answer
a)
Equation describing the trajectory of the particle:
\[y\,=\,4-\left(\frac{4}{3}\right)x\,,\] \[x\,\geq\,0\,,\] \[z\,=\,0\,.\]The trajectory is a straight line in the xy plane.
b)
c)
\[s\,=\,25\left(t_{k2}^{2}-t_{k1}^{2}\right)\,.\]d)
\[s\,=\,25\left(t_2^{2}-t_1^{2}\right)\,=\,5\,\mathrm{m}\,,\]Where:
\(t_1\,=\,0\,\mathrm{s}\hspace{15px}\) is time of crossing the y axis
\(t_2\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\hspace{15px}\) is time of crossing the y axis
Or from the picture showing the trajectory:
\[s\,=\,\sqrt{4^{2}+3^{2}}\,\mathrm{m}\,=\,5\,\mathrm{m}\,.\]e)
\[\Delta{t}\,=\,t_2-t_1\,,\] \[\Delta{t}\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\,.\]f)
\[v\,=\,\frac{\Delta{s}}{\Delta{t}}\,=\,5\sqrt{5}\,\mathrm{m\,s^{-1}}\,,\]g)
The stated formula generally holds for any function v that is a linear function of time.
It can therefore be used in our scenario:
\[v_\mathrm{a}\,=\,\frac{(v_1+v_2)}{2}\,=\,5\sqrt{5}\,\mathrm{m\,s^{-1}}\,.\]