A Moving Wheel
Task number: 1159
A wheel with a radius R moves in a rectilinear motion with a speed of v0. In the coordinate system related to the ground:
a) find the progress of the position vector of point X on the circumference of the wheel,
b) find the progress of the speed of point X and the progress of its magnitude,
c) using the result a) draw the shape of the trajectory and solve the length of one of its curves,
d) find the length of the travelled distance depending on time.
Hint 1: The picture of the situation
Choose the appropriate coordinate axes and the origin of the coordinate system.
Draw the situation for the time t = 0 s. Choose the beginning position of point X in the origin of the coordinate system.
Then draw the situation for the time t and mark the position of point X where the wheel gets in time t.
Mark the position of point X in the figure which the wheel achieved in time t. What is the distance?
Hint 2 for a): The progress of the position vector
Decompose the motion of point X in the direction of the x-axis and in the rotation around point S.
Try to find three simple vectors by which we can write the position vector \(\vec{PX}\).
Hint 3 for b) The progress of the speed and the progress of its magnitude
How do we get from the progress of the position vector of point X the progress of the speed of point X? Write them.
How do we find the progress of the magnitude of the speed of point X?
Hint 4 for c): The trajectory of the motion, the length of the arc
Determine the shape of the progress of the speed from the progress of the motion vector of point X.
Draw the picture.
Knowing the progress of the magnitude of the speed how do we calculate the length of a single arc or the travelled distance for one revolution?
Hint 5 for d): The travelled distance as a function of time
We know what distance point X travels for one period.
We can calculate the travelled distance (for the time t < T) by the equation for the progress of the speed.
How do we express the total travelled distance in the random time t?
Complete solution
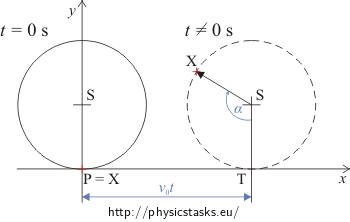
The picture of the situation:
We set off the stopwatch (t = 0 s) for example in the moment where point X touches the pavement. We choose this point on the pavement to be the origin of the coordinate system (denoted by P). We point the x-axis axis in the direction of the motion of the wheel along the pavement and y-axis vertically upward.
The picture shows the situation in time t = 0 s.
The wheel covers the distance v0t in the direction of x-axis and the situation is created showing in the second picture.
The point X is relocated from the origin P to the left upward. If the wheel doesn´t slip, the arc TX has the same length as the rolled distance v0t. This angle α (corresponding to the arc TSX) is given:
\[\alpha\,=\, -\omega{t}\,=\, -\frac{v_0t}{R}\]a) The position vector
The position vector \(\vec{PX}\,=\,\vec{r}\left(t\right)\) is changed quite complicatedly. It stretches right and is in rotation upward and downward. We can compose this vector from three vectors which behave more easily:
\[\vec{PX}\,=\,\vec{PT}+\vec{TS}+\vec{SX}\]where \(\vec{PT}\) … vector stretches along x-axis with velocity v0: \(\vec{PT}\,=\,v_0t\vec{\,i\,}\)
\(\vec{TS}\) … vector is in the direction of y-axis: \(\vec{TS}\,=\,R\vec{\,j\,}\)
\(\vec{SX}\) … vector rotates equally in the direction clockwise around point S.
\[\vec{SX}\,=\,R\cos\left(-\frac{v_0t}{R}-\frac{\pi}{2}\right)\vec{\,i\,}+R\sin\left(-\frac{v_0t}{R}-\frac{\pi}{2}\right)\vec{\,j\,}\]where \(\left(-\frac{v_0t}{R}-\frac{\pi}{2}\right)\) is the angle which the vector \(\vec{SX}\) forms to x-axis.
We substitute into the equation:
\[\vec{PX}\,=\,\vec{PT}+\vec{TS}+\vec{SX}\]and we use these equations:
\[\cos\left(-\alpha-\frac{\pi}{2}\right)\,=\,-\sin\alpha\] \[\sin\left(-\alpha-\frac{\pi}{2}\right)\,=\,-\cos\alpha\]then we get for the motion vector \(\vec{r}\left(t\right) \,=\, \vec{PX}\):
\[\vec{PX}\,=\,\left(v_0t-R\sin\frac{v_0t}{R}\right)\vec{\,i\,}+\left(R-R\cos\frac{v_0t}{R}\right)\vec{\,j\,}\]alternatively for the components:
\[x\,=\,v_0t-R\sin\frac{v_0t}{R}\] \[y\,=\,R-R\cos\frac{v_0t}{R}\] \[z\,=\,0\]b) The progress of the speed and the progress of its magnitude
We determine the progress of the speed \(\vec{v}\left(t\right)\) by the derivative of the function \(\vec{r}\left(t\right)\):
\[\vec{r}\left(t\right) \,=\, \vec{PX}\,=\,\left(v_0t-R\sin\frac{v_0t}{R}\right)\vec{\,i\,}+\left(R-R\cos\frac{v_0t}{R}\right)\vec{\,j\,}\] \[\vec{v}\left(t\right)\,=\,\frac{\mathrm{d}\left(v_0t-R\sin\frac{v_0t}{R}\right)}{\mathrm{d}t}\vec{\,i\,}+\frac{\mathrm{d}\left(R-R\cos\frac{v_0t}{R}\right)}{\mathrm{d}t}\vec{\,j\,}\]After the derivative we get for the progress of the speed:
\[\vec{v}\left(t\right)\,=\,\left(v_0-v_0\cos\frac{v_0t}{R}\right)\vec{\,i\,}+v_0\sin\frac{v_0t}{R}\vec{\,j\,}\]The magnitude of the speed is the absolute value of this vector:
\[v\left(t\right)\,=\,\left|\vec{v}\left(t\right)\right|\,=\,\sqrt{v_x^{2}+v_y^{2}+v_z^{2}}\,=\,\sqrt{\left(v_0-v_0\cos\frac{v_0t}{R}\right)^{2}+ \left(v_0\sin\frac{v_0t}{R}\right)^{2}}\] \[v\left(t\right)\,=\, \sqrt{v_0^2 - 2v_0^2{{\cos}^2\left(\frac{v_0t}{R}\right)} + v_0^{2}\left({\cos}^{2}\left(\frac{v_0t}{R}\right) + {\sin}^{2}\left(\frac{v_0t}{R}\right)\right)}\] \[v(t)= \sqrt{2v_0^{2} - 2v_0^{2}{\cos}^{2}(\frac{v_0t}{R})}\] \[v\left(t\right)\,=\, 2v_0\sqrt{\frac{1-\cos\frac{v_0t}{R}}{2}}\]Or we use this equation: \(\left|\sin\frac{\alpha}{2}\right|\,=\,\sqrt{\frac{1-\cos\alpha}{2}}\) and so simply:
\[v\left(t\right)\,=\,2v_0\left|\sin\frac{v_0}{2R}t\right|\]c) The trajectory of the motion, the length of the arc
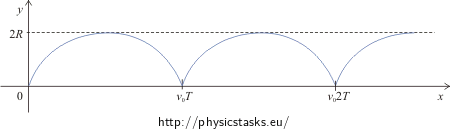
We determine the trajectory in the most comfortable way for example from the components of the vector \(\vec{PX}\):
\[x\,=\,v_0t-R\sin\frac{v_0t}{R}\] \[y\,=\,R-R\cos\frac{v_0t}{R}\] \[z\,=\,0\]We determine a few points of the trajectory (x, y) for example in these times 0, \(\frac{T}{6}\), \(\frac{2T}{6}\), \(\frac{3T}{6}\) etc.
We assume a facilitation for the numerical calculation \(R\,=\,1\,\mathrm{m}\) a \(v\,=\,1\,\mathrm{m\,s^{-1}}\).
From these equations:
\[ x\,=\,v_0t-R\sin\frac{v_0t}{R}\] \[y\,=\,R-R\cos\frac{v_0t}{R}\] \[z\,=\,0\]We get then:
x 0 0.18 1.23 3.13 5.05 6.10 6.28 y 0 0.5 1.5 2.0 1.5 0.5 0 The length of the single arc equals the travelled distance of the point during one period and so:
\[s_T\,=\,\int_0^{T}{v(t)}\,\mathrm{d}t\]Where \(v\left(t\right) \,=\, 2v_0\left|\sin\frac{v_0}{2R}t\right|\)
One period equals \(T\,=\,\frac{2\pi{R}}{v_0}\). This expression \(\sin\frac{v_0}{2R}t\) assumes (on the whole interval 0 do T) positive values therefore we don´t write necessarily the absolute value.
\[s_T\,=\,\int_0^{T}\left({2v_0\sin\frac{v_0}{2R}t}\right)\mathrm{d}t \,=\, 2v_0\frac{2R}{v_0}\left[-\cos\frac{v_0t}{2R}\right]_0^{T}\] \[s_T \,=\, 4R\left(-\cos\frac{v_02\pi{R}}{2Rv_0} + 1\right) \,=\, 8R \]The length of the single arc is equalled this expression: \(s_T \,=\, 8R\).
d) The travelled distance as a function of time
We get the total distance for the rolling of much more than one revolution as the sum of the distance of complete revolutions and the rest of the revolution.
We know the length of one arc is \(s_T\,=\,8R\).
The distance of the complete revolution equals:
\[s_c\,=\,\left(INT\frac{t}{T}\right)\cdot 8R\]where \(INT\frac{t}{T}\) is the whole-number of the part quotient \(\frac{t}{T}\).
We calculate the rest of the distance from the equation:
\[s_z\,=\,\int_0^{t_z}{v(t)}\,\mathrm{d}t\]where \(v\left(t\right) \,=\, 2v_0\left|\sin\frac{v_0}{2R}t\right|.\)
One period equals \(T\,=\,\frac{2\pi{R}}{v_0}\). This expression \(\sin\frac{v_0}{2R}t\) assumes (on the whole interval 0 do T) positive values and tz < T therefore we don´t write necessarily the absolute value.
\[s_z\,=\,\int_0^{t_z}{2v_0\left|\sin\frac{v_0}{2R}t\right|}\mathrm{d}t\,=\,2v_0\frac{2R}{v_0}\left[-\cos\frac{v_0t}{2R}\right]_0^{t_z}\] \[s_z\, =\,4 R\left(1-\cos\frac{v_0t_z}{2R}\right)\,=\,8R\sin^{2}\frac{v_0t_z}{4R}\]The total travelled distance in the time t equals:
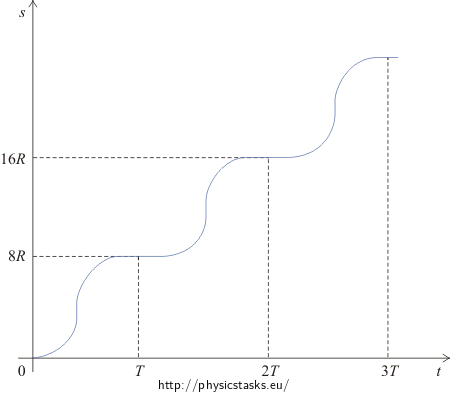
\[s\left(t\right)\,=\,\left(INT\frac{t}{T}\right)\cdot 8R+8R\sin^{2}\frac{v_0t_z}{4R}\]The first member presents sums of the completed arcs and the second member presents the last incomplete arc.
The graph of the function \(s\left(t\right)\,=\,\left(INT\frac{t}{T}\right)\cdot 8R+8R\sin^{2}\frac{v_0t_z}{4R}\) looks like (see the figure):
Answer
a) It holds for the progress of the position vector of point X (which is on the circumference of the wheel):
\[\vec{r}\left(t\right) \,=\, \vec{PX}\,=\,\left(v_0t-R\sin\frac{v_0t}{R}\right)\vec{\,i\,}+\left(R-R\cos\frac{v_0t}{R}\right)\vec{\,j\,}\]alternatively for the components:
\[x\left(t\right) \,=\, v_0t-R\sin\frac{v_0t}{R}\] \[y\left(t\right) \,=\, R-R\cos\frac{v_0t}{R}\] \[z\left(t\right) \,=\, 0\]b) It holds for the progress of the speed of point X
\[\vec{v}\left(t\right)\,=\,\left(v_0-v_0\cos\frac{v_0t}{R}\right)\vec{\,i\,}+v_0\sin\frac{v_0t}{R}\vec{\,j\,}\]The magnitude of the speed of point X is:
\[v\left(t\right)\,=\,\left|\vec{v}\left(t\right)\right|\,=\,\sqrt{v_x^{2}+v_y^{2}+v_z^{2}}\,=\,2v_0\left|\sin\frac{v_0}{2R}t\right|\]c)The shape of the trajectory is:
The length of the single arc is: \(s_T\,=\, 8R\)
d) The length of the total arc is:
\[s\left(t\right)\,=\,\left(INT\frac{t}{T}\right)\cdot 8R+8R\sin^{2}\frac{v_0t_z}{4R}\]where \(INT\frac{t}{T}\) is the whole-number of the part quotient \(\frac{t}{T}\) and \(t_z \,=\,t - \left(INT\frac{t}{T}\right)T\)
(The first member presents sums of the completed arcs and the second member presents the last incomplete arc)