Collection of Solved Problems in Physics

Bullet in Vacuum

Task number: 1991

• Hint 1: Free body diagram

  Draw a free body diagram illustrating the situation and mark coordinate axes x and y into it.

  Draw the vector of the initial velocity of the bullet \(\vec{v}_0\) and its velocity \(\vec{v}\) at an arbitrary point of its motion trajectory as well as its components in directions of the coordinate axes.

• Solution of Hint 1

  A free body diagram illustrating the situation:

  

• Hint 2: Behaviour of speed

  Think about what kinds of motion the bullet follows in directions of the coordinate axes.

  First, express the components of the velocity of the bullet v_x, v_y. The behaviour of the speed of the bullet can be easily determined from them.

• Solution of Hint 2

  In the direction of the x axis: a uniform linear motion with speed v₀.

  In the direction of the y axis: a free fall

  Components of velocity (in directions of the x axis and the y axis):

  \[v_x\,=\,v_0\,,\] \[v_y\,=\,gt\,.\]

  Behaviour of speed

  \[v(t) \,=\, \sqrt{v_x^{2}\,+\,v_y^{2}}\,=\,\sqrt{v_0^{2}\,+\,g^{2}t^{2}}\,.\]

• Hint 3: Magnitude of tangential acceleration

  Use the knowledge of the speed of the bullet from the previous hint. How can you use it to express the magnitude of the tangential acceleration of the bullet?

• Solution of Hint 3

  We obtain the magnitude of tangential acceleration by differentiating speed with respect to time:

  \[a_t\,=\,\frac{\mathrm{d}v}{\mathrm{d}t}\,=\,\frac{\mathrm{d}\left(\sqrt{v_0^{2}\,+\,g^{2}t^{2}}\right)}{\mathrm{d}t}\,=\,\frac{g^{2}t}{ \sqrt{v_0^{2}\,+\,g^{2}t^{2}}}\,.\]

• Hint 4: Magnitude of normal acceleration

  To determine the magnitude of the normal (centripedal) acceleration of the bullet you need the magnitude of its tangential acceleration (known from the previous hint) as well as the magnitude of its net acceleration, which you can obtain from the components of acceleration a_x, a_y in directions of the coordinate axes.

  What relation holds between the net, tangential and normal accelerations of the bullet?

• Solution of Hint 4

  Components of acceleration:

  \[a_\mathrm{x}\,=\,\frac{\mathrm{d}v_\mathrm{x}}{dt}\,=\,\frac{\mathrm{d }\left(v_0\right)}{\mathrm{d}t} \,=\, 0\,,\] \[a_\mathrm{y}\,=\,\frac{\mathrm{d}v_\mathrm{y}}{\mathrm{d}t}\,=\, \frac{\mathrm{d}\left(gt\right)}{\mathrm{d}t} \,=\, g\,,\] \[a \,=\, \sqrt{a_\mathrm{x}^{2}+ a_\mathrm{y}^{2}} \,=\, g\,.\]

  We obtain the magnitude of normal acceleration from relation:

  \[a\,=\,\sqrt{a_\mathrm{t}^{2}+ a_\mathrm{n}^{2}}\,.\]

  From here:

  

  \[a_\mathrm{n}\,=\,\sqrt{a^{2}-a_\mathrm{t}^{2}}\,,\] \[a_\mathrm{n}\,=\,\sqrt{g^{2}-\frac{g^{4}t^{2}}{v_0^{2}+g^{2}t^{2}}} \,=\, \sqrt{\frac{g^{2}v_0^{2}}{v_0^{2}+g^{2}t^{2}}}\,,\] \[a_\mathrm{n}\,=\,\frac{gv_0}{\sqrt{v_0^{2}+g^{2}t^{2}}}\,.\]

• Hint 5: Radius of the trajectory curvature

  The trajectory of the bullet is drawn in the free body diagram.

  What is the relation between the radius of curvature of the trajectory, the speed and the magnitude of the normal acceleration of the bullet?

• Solution of Hint 5

  For the magnitude of normal acceleration it holds that:

  \[a_n \,=\,\frac{v^{2}}{\rho}\,.\]

  It therefore holds for the radius of curvature that:

  \[\rho\,=\,\frac{v^{2}}{a_n}\,,\]

  where

  \[v \,=\, \sqrt{v_0^{2}+g^{2}t^{2}}\,,\] \[a_n\,=\,\frac{gv_0}{\sqrt{v_0^{2}+g^{2}t^{2}}}\,.\] \[\rho(t)\,=\,\frac{ (v_0^{2}+g^{2}t^{2})\sqrt{v_0^{2}+g^{2}t^{2}}}{gv_0}\,=\,\frac{\sqrt{( v_0^{2}+g^{2}t^{2})^{3}}}{gv_0}\,.\]

• OVERALL SOLUTION

  A free body diagram illustrating the situation:

  

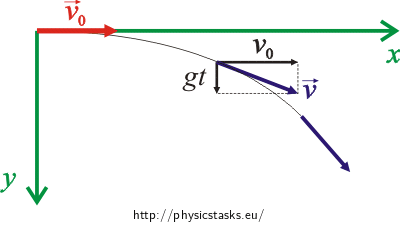
  In the direction of the x axis: a uniform linear motion with speed v₀.

  In the direction of the y axis: a free fall

  Components of velocity (in directions of the x axis and the y axis):

  \[v_\mathrm{x}\,=\,v_0\,,\] \[v_\mathrm{y}\,=\,gt\,.\]

  Behaviour of speed

  \[v(t) \,=\, \sqrt{v_\mathrm{x}^{2}\,+\,v_\mathrm{y}^{2}}\,=\,\sqrt{v_0^{2}\,+\,g^{2}t^{2}}\,.\]

  Magnitude of the tangential acceleration:

  We obtain the magnitude of tangential acceleration by differentiating speed with respect to time:

  \[a_\mathrm{t}\,=\,\frac{\mathrm{d}v}{\mathrm{d}t}\,=\,\frac{\mathrm{d}\left(\sqrt{v_0^{2}\,+\,g^{2}t^{2}}\right)}{\mathrm{d}t}\,=\,\frac{g^{2}t}{ \sqrt{v_0^{2}\,+\,g^{2}t^{2}}}\,.\]

  Magnitude of the net acceleration

  We obtain the magnitude of normal acceleration from relation:

  \[a\,=\,\sqrt{a_\mathrm{t}^{2}+ a_\mathrm{n}^{2}}\,.\]

  From here:

  \[a_\mathrm{n}\,=\,\sqrt{a^{2}-a_\mathrm{t}^{2}}\,,\]

  Components of acceleration:

  \[a_\mathrm{x}\,=\,\frac{\mathrm{d}v_\mathrm{x}}{dt}\,=\,\frac{\mathrm{d }\left(v_0\right)}{\mathrm{d}t} \,=\, 0\,,\] \[a_\mathrm{y}\,=\,\frac{\mathrm{d}v_\mathrm{y}}{\mathrm{d}t}\,=\, \frac{\mathrm{d}\left(gt\right)}{\mathrm{d}t} \,=\, g\,,\]

  

  \[a \,=\, \sqrt{a_\mathrm{x}^{2}+ a_\mathrm{y}^{2}} \,=\, g\,.\] \[a_\mathrm{n}\,=\,\sqrt{g^{2}-\frac{g^{4}t^{2}}{v_0^{2}+g^{2}t^{2}}} \,=\, \sqrt{\frac{g^{2}v_0^{2}}{v_0^{2}+g^{2}t^{2}}}\,,\] \[a_\mathrm{n}\,=\,\frac{gv_0}{\sqrt{v_0^{2}+g^{2}t^{2}}}\, .\]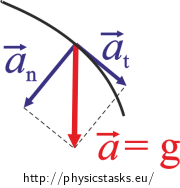

  Radius of the trajectory curvature:

  For the magnitude of normal acceleration it holds that:

  \[a_\mathrm{n} \,=\,\frac{v^{2}}{\rho}\,.\]

  It therefore holds for the radius of curvature that:

  \[\rho\,=\,\frac{v^{2}}{a_\mathrm{n}}\,,\]

  where

  \[v \,=\, \sqrt{v_0^{2}+g^{2}t^{2}}\,,\] \[a_\mathrm{n}\,=\,\frac{gv_0}{\sqrt{v_0^{2}+g^{2}t^{2}}}\,.\] \[\rho(t)\,=\,\frac{ (v_0^{2}+g^{2}t^{2})\sqrt{v_0^{2}+g^{2}t^{2}}}{gv_0}\,=\,\frac{\sqrt{( v_0^{2}+g^{2}t^{2})^{3}}}{gv_0}\,.\]

• Answer

  The behaviour of the speed of the bullet is

  \[v(t) \,=\, \sqrt{v_0^{2}+g^{2}t^{2}}\,.\]

  The magnitude of the tangential acceleration of the bullet is

  \[a_\mathrm{t}(t) \,=\, \frac{g^{2}t}{ \sqrt{v_0^{2}+g^{2}t^{2}}}\,.\]

  The magnitude of the normal acceleration of the bullet is

  \[a_\mathrm{n}(t) \,=\, \frac{gv_0}{\sqrt{v_0^{2}+g^{2}t^{2}}}\,.\]

  It holds for the radius of the trajectory curvature of the bullet that

  \[\rho(t) \,=\, \frac{\sqrt{( v_0^{2}+g^{2}t^{2})^{3}}}{v_0g}\,.\]