Collection of Solved Problems in Physics

The Moment of Inertia of Two Balls

Task number: 1160

• Notation

  m1	Mass of the first ball
  m2	Mass of the second ball
  L	The length of the connecting rod
  I0 = ?	The moment of inertia of the system about the axis passing through the centre of gravity

• Hint 1

  Draw the situation at the beginning and position the appropriate coordinate system. Write the corresponding coordinates of both balls into the figure. Thanks to the fact that their sizes were not defined, we can consider both of the balls to be mass points with masses centralized in the centres of gravity of the original balls.

• Solution to Hint 1

  The figure shows the appropriate position which we will work with. Both balls lie on the x-axis, one of them is located directly in the origin of the coordinate system.

  

  Coordinates of mass points A and B (which substitute the balls) in our case are:

  \[A\,=\,[0{,}0]\] \[B\,=\,[L,0]\]

• Hint 2

  To find the moment of inertia I_o of the system about the axis passing through the centre of gravity, we must find the first coordinate of the centre of gravity CG of the system. What is the relation for the position vector of the centre of gravity of a system of mass points?

  Is it possible to determine one component of the centre of gravity at once without any calculation?

• Solution to Hint 2

  The relation (for the position of the centre of gravity of n mass points) appears as follows

  \[\vec{r}_T\,=\,\frac{\sum_{i=1}^n{m_i\vec{r}_i}}{\sum_{i=1}^n{m_i}}\]

  where m_i are individual masses of mass points and r_i are their corresponding position vectors.

  Based on the fact that the coordinates of the centre of gravity can be calculated as compomnents, the x coordinate of the centre of gravity is defined:

  \[x_T\,=\,\frac{\sum_{i=1}^n{m_ix_i}}{\sum_{i=1}^n{m_i}}\,=\,\frac{m_1{\cdot}0\,+\,m_2{\cdot}L}{m_1\,+\,m_2}\,=\,\frac{m_2L}{m_1\,+\,m_2}\tag{1}\]

  The procedure mentioned above can be applied the same way for y coordinate of the centre of gravity, however, the result is obvious: the y coordinate equals y_T = 0 for both of the balls.

• Hint 3

  Determine the distance of the individual balls (mass points A and B) from the center of gravity of the system. Are we able to determine the unknown moment of inertia using their positions? Determine the moment of inertia.

• Solution to Hint 3

  As can be seen in the figure, the distance of point A from the centre of gravity of the system is x_T and the distance of point B from the centre of gravity of the system is L - x_T. The distance from the centre of gravity means the distance from the axis o which is perpendicular to the rod and passes through the centre of gravity. We have everything what we need to determine the moment of inertia I_o.

  Do not forget that the moment of inertia of system of n mass points about an axis is given by the following relationship:

  \[I\,=\,\sum_{i\,=\,1}^n{m_ir_i^2}\]

  where m_i are masses of individual mass points and r_i are their distances from the given axis. In this case it is about axis o and it is given:

  \[I_\mathrm{o}\,=\,m_\mathrm{1}x_\mathrm{T}^2\,+\,m_\mathrm{2}(L\,-\,x_\mathrm{T})^2\tag{2}\]

  We substitute for x_T from equation (1) and get:

  \[I_\mathrm{o}\,=\,m_\mathrm{1}(\frac{m_\mathrm{2L}}{m_\mathrm{1}\,+\,m_\mathrm{2}})^2\,+\,m_\mathrm{2}(L\,-\,\frac{m_\mathrm{2}L}{m_\mathrm{1}\,+\,m_\mathrm{2}})^2\] \[I_\mathrm{o}\,=\,\frac{m_\mathrm{1}m_\mathrm{2}^2L^2}{(m_\mathrm{1}\,+\,m_\mathrm{2})^2}\,+\,m_\mathrm{2}L^2(1\,-\,\frac{m_\mathrm{2}}{m_\mathrm{1}\,+\,m_\mathrm{2}})^2\] \[I_\mathrm{o}\,=\,\frac{m_\mathrm{1}m_\mathrm{2}^2L^2}{(m_\mathrm{1}\,+\,m_\mathrm{2})^2}\,+\,\frac{m_\mathrm{2}L^2m_\mathrm{1}^2}{(m_\mathrm{1}\,+\,m_\mathrm{2})^2}\,=\frac{m_\mathrm{1}m_\mathrm{2}L^2(m_\mathrm{1}\,+\,m_\mathrm{2})}{(m_\mathrm{1}\,+\,m_\mathrm{2})^2}\] \[I_\mathrm{o}\,=\,\frac{m_\mathrm{1}m_\mathrm{2}L^2}{m_\mathrm{1}\,+\,m_\mathrm{2}}\]

• Complete solution

  Thanks to the fact that their sizes were not defined, we can consider both of the balls to be mass points with masses centralized in the centres gravity of the original balls.

  The figure shows our situation placed appropriately into the coordinates system. Both balls lie on the x-axis; one of them is located directly in the origin of the coordinate system.

  

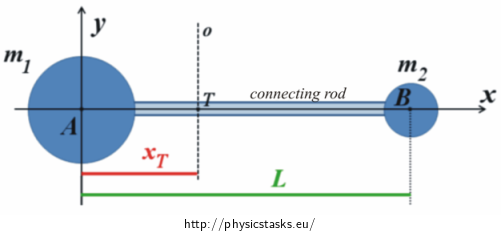
  Coordinates of mass points A and B (which substitute the balls) in our case are:

  \[A\,=\,[0{,}0]\] \[B\,=\,[L,0]\]

  First we have to determine the position of the centre of gravity, because we need to find the moment of inertia about the axis passing through the centre of gravity. The relation (for the position of the centre of gravity of n mass points) appears as follows \[\vec{r}_\mathrm{T}\,=\,\frac{\sum_{i=1}^n{m_i\vec{r}_i}}{\sum_{i=1}^n{m_i}}\] where m_i are individual masses of mass points and r_i are their corresponding position vectors. Based on the fact that the coordinates of the centre of gravity can be calculated as compomnents, the x coordinate of the centre of gravity is defined:

  \[x_\mathrm{T}\,=\,\frac{\sum_{i=1}^n{m_ix_i}}{\sum_{i=1}^n{m_i}}\,=\,\frac{m_\mathrm{1}{\cdot}0\,+\,m_\mathrm{2}{\cdot}L}{m_\mathrm{1}\,+\,m_\mathrm{2}}\,=\,\frac{m_\mathrm{2}L}{m_\mathrm{1}\,+\,m_\mathrm{2}}\tag{1}\]

  The procedure mentioned above can be applied the same way for y coordinate of the centre of gravity, however, the result is obvious: the y coordinate is y_T = 0 for both of the balls.

  As can be seen from the figure, the distance of point A from the centre of gravity of the system is x_T and the distance of point B from the centre of gravity of the system is L - x_T. The distance from the centre of gravity means the distance from the axis o which is perpendicular to the rod and passes through the centre of gravity. We have everything what we need to determine the moment of inertia I_o.

  Do not forget that the moment of inertia of a system of n mass points about an axis is determined as follows

  \[I\,=\,\sum_{i\,=\,1}^n{m_ir_i^2}\]

  where m_i are the masses of individual mass points and r_i are their distances from the given axis. In this case it is about axis o and it is given:

  \[I_\mathrm{o}\,=\,m_\mathrm{1}x_\mathrm{T}^2\,+\,m_\mathrm{2}(L\,-\,x_\mathrm{T})^2\tag{2}\]

  We substitute for x_T from equation (1) and get:

  \[I_\mathrm{o}\,=\,m_\mathrm{1}(\frac{m_\mathrm{2}L}{m_\mathrm{1}\,+\,m_\mathrm{2}})^2\,+\,m_\mathrm{2}(L\,-\,\frac{m_\mathrm{2}L}{m_\mathrm{1}\,+\,m_\mathrm{2}})^2\] \[I_\mathrm{o}\,=\,\frac{m_\mathrm{1}m_\mathrm{2}^2L^2}{(m_\mathrm{1}\,+\,m_\mathrm{2})^2}\,+\,m_\mathrm{2}L^2(1\,-\,\frac{m_\mathrm{2}}{m_\mathrm{1}\,+\,m_\mathrm{2}})^2\] \[I_\mathrm{o}\,=\,\frac{m_\mathrm{1}m_\mathrm{2}^2L^2}{(m_\mathrm{1}\,+\,m_\mathrm{2})^2}\,+\,\frac{m_\mathrm{2}L^2m_\mathrm{1}^2}{(m_\mathrm{1}\,+\,m_\mathrm{2})^2}\,=\frac{m_\mathrm{1}m_\mathrm{2}L^2(m_\mathrm{1}\,+\,m_\mathrm{2})}{(m_\mathrm{1}\,+\,m_\mathrm{2})^2}\] \[I_\mathrm{o}\,=\,\frac{m_\mathrm{1}m_\mathrm{2}L^2}{m_\mathrm{1}\,+\,m_\mathrm{2}}\]

• Answer

  The moment of inertia I_o of the mentioned system about the axis o passing through the centre of its gravity is:

  \[I_\mathrm{o}\,=\,\frac{m_\mathrm{1}m_\mathrm{2}L^2}{m_\mathrm{1}\,+\,m_\mathrm{2}}\]