Cubes banded by fibers
Task number: 1524
Three cubes weighing m1, m2 and m3 are mutually banded by fibers, as shown in the igure. The coefficient of friction between all contact surfaces is identical and has a value of f. Determine the acceleration of cubes and tensile force tensioning both fibres. Do not consider the weight of the pulleys and the fiber.
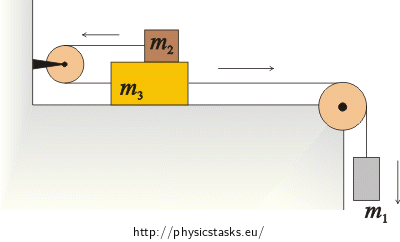
Notation
m1 mass of cube number one m2 mass of cube number two m3 mass of cube number three f friction coefficient for every arbitrary contact a = ? acceleration of cubes T1 = ? tensile force stretching the fibre between cubes m2 and m3 T2 = ? tensile force stretching the fibre between cubes m3 and m1 Hint 1 – forces acting on the individual cubes, motion equations
Be aware of the forces acting on the individual cubes and type equation of motion for each of them.
Recommendation: For clarity, draw a figure in which you will draw the forces acting on the cubes. Draw the figures for each of the cubes separately.
Hint 2 – scalar equations of motion, the relationship among tensile forces in fibers, frictional forces and pressure forces
Choose the appropriate coordinate system and rewrite the scalar equations of motion. Recognize what relationships are among some tensile, frictional and pressure forces – Use 3rd Newton’s law.
Hint 3 – frictional forces
Be aware of what the value of frictional force depends on and how it can be expressed. Quantify frictional forces \(F_{t_2}\) and \(F_{t_3}\).
Hint 4 – Calculation of acceleration and tensile forces in fibres
Use equation (1), (2) and (6). After substituting for frictional forces you get three equations with three unknowns. Calculate the values of acceleration and tension forces T1 and T2 in fibres.
TOTAL SOLUTION
We draw the forces acting on the cubes to the figure at first and write the equations of motion for them.
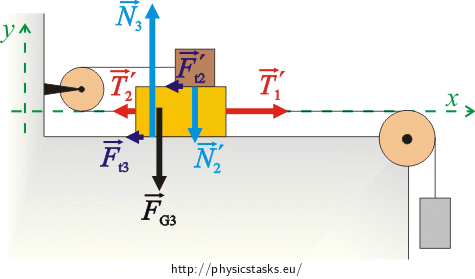
The forces acting on the cubes:
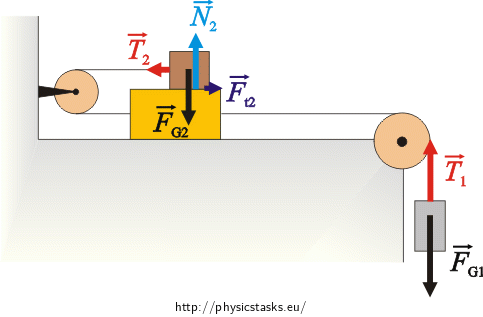
Cube m1:
\(\vec{F}_{G_1}\)…weight force
\(\vec{T}_{1}\)…tensile force the fibre is acting on the cube
Cube m2:
\(\vec{F}_{G_2}\)…weight force
\(\vec{N}_{2}\)…compressive force which the cube m2 pushes the cube m3 with
\(\vec{T}_{2}\)…tensile force the fibre is acting on the cube with
\(\vec{F}_{t_2}\)…frictional force between the cubes m2 and m3
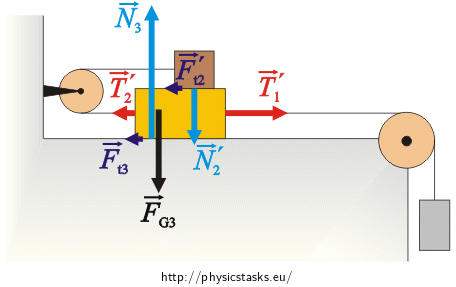
Cube m3:
\(\vec{F}_{G_3}\)…weight force
\(\vec{T}_{2}\prime\)…tensile force the fibre is acting on the cube
\(\vec{T}_{1}\prime\)…tensile force the fibre is acting on the cube
\(\vec{F}_{t_3}\)…frictional force between the cube and the ground
\(\vec{F}_{t_2}\prime\)…frictional force between the cubes m2 and m3
\(\vec{N}_{2}\prime\)…compressive force which the cube m3 pushes cube m2 with
\(\vec{N}_{3}\)…compressive force which the cube the ground with
The equations of motion for each cube:
All three cubes are interconnected by fibres, moving with the same acceleration
\[m_1:\qquad \vec{F}_{G_1} + \vec{T}_1=m_1\vec{a}\] \[m_2:\qquad \vec{F}_{G_2}+\vec{N}_2+\vec{F}_{t_2}+ \vec{T}_2=m_2\vec{a}\] \[m_3:\qquad \vec{F}_{G_3}+\vec{T}_1\prime +\vec{T}_2\prime+\vec{N}_3+\vec{N}_2\prime+\vec{F}_{t_3}+\vec{F}_{t_2}\prime=m_3\vec{a}\]To rewrite the equations of motion as a scalar equation, we choose a coordinate system x, y so that the x-axis goes along the direction of movement of the cubes. The y-axis is perpendicular to the x-axis.
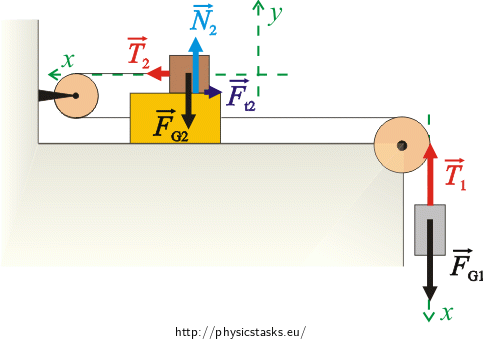
Scalar equation of motion:
Cube m1:
\[x:\qquad F_{G_1} - T_1\,=\,m_1a\tag{1}\]Cube m2:
\[x:\qquad T_2-F_{t_2}\,=\,m_2a\tag{2}\] \[y:\qquad N_2-F_{G_2}\,=\,0\tag{3}\]Cube m3:
\[x:\qquad T_1\prime-T_2\prime-F_{t_3}-F_{t_2}\prime\,=\,m_3a\tag{4}\] \[y:\qquad N_3-N_2\prime-F_{G_3}\,=\,0\tag{5}\]The cubes do not move in the y direction, so the acceleration is zero.
Tensile forces in the fibres:
Since we neglect the weight of the pulleys, thus they have no inertia and do not affect the tensile forces in fibres. Cube m3 acts cube m2 through the fibre and contrariwise cube m2 acts on cube m3. Similarly, with the cube m1 acts on cube m3. According to the Newton’s third Law it applies for the value of the forces:
\[|\vec{T}_1| \,=\, |\vec{T}_1\prime|\] \[|\vec{T}_2| \,=\, |\vec{T}_2\prime|\]Frictional forces:
Frictional force of cube m3 acts on cube m2 and contrariwise frictional force of cube m2 acts on cube m3 in the opposite direction. It applies according to the Newton’s third Law:
\[|\vec{F}_{t_2}| \,=\, |\vec{F}_{t_2}\prime|\]
Compressive forces:
Compressive force of cube m3 acts on cube m2 and contrariwise compressive force of cube m2 acts on cube m3 in the opposite direction. It applies according to the Newton’s third Law:
\[|\vec{N}_2| \,=\, |\vec{N}_2\prime|\]We rewrite the equations (4) and (5):
\[x:\qquad T_1-T_2-F_{t_3}-F_{t_2}\,=\,m_3a\tag{6}\] \[y:\qquad N_3-N_2-F_{G_3}\,=\,0\tag{7}\]Expression of friction forces:
Frictional force \(F_{t_2}\) is proportional to the force which cube m2 pushes cube m3 with, that is, according to Newton’s third law as large, as the force which the cube m3 pushes cube m2 with.
Frictional force \(F_{t_2}\) can be expressed as:
\[F_{t_2} \,=\, N_2f\]Substituting for \(N_2\) from the equation (3):
\[F_{t_2} \,=\, F_{G_2}f\,=\,m_2gf\tag{8}\]Frictional force \(F_{t_3}\) is proportional to the force which cube m3 affects the table with, that is, according to Newton’s third law as large, as the force which the table affects cube m3.
Frictional force \(F_{t_3}\) can be expressed as:
\[F_{t_3} \,=\, N_3f\]
Substituting for \(N_3\) from the equation (7):
\[F_{t_3} \,=\, (N_2+F_{G_3)}f\,=\,(F_{G_2}+F_{G_3})f\] \[F_{t_3} \,=\, (m_2+m_3)gf\tag{9}\]We rewrite the equation (1), (2) and (6) into equation (2), substitute the frictional force \(F_{t_2}\) and to the equation (6) substitute the frictional forces \(F_{t_2}\) and \(F_{t_3}\):
\[m_1g - T_1\,=\,m_1a\tag{10}\] \[T_2-m_2gf\,=\,m_2a\tag{11}\] \[T_1-T_2-(m_2+m_3)gf-m_2gf\,=\,m_3a\tag{12}\]Calculation of acceleration:
We count the equations (10) – (12) up.
\[m_1g-m_2gf-m_3gf-2m_2gf\,=\,\left(m_3+m_2+m_1\right)a\] \[m_1g-m_3gf-3m_2gf\,=\,\left(m_3+m_2+m_1\right)a\]\[a\,=\,\frac{g\left(m_1-m_3f-3m_2f\right)}{m_3+m_2+m_1}\tag{13}\]
Calculation of tensile force T1:
We express the force T1 from equation (10):
\[T_1\,=\,m_1g-m_1a\,=\,m_1g-m_1\frac{m_1g-m_3gf-3m_2gf}{m_3+m_2+m_1}\]
We convert it to the last common denominator:
\[T_1\,=\,\frac{m_1^2g+m_1m_2g+m_1m_3g-m_1^2g+m_1m_3gf+3m_1m_2gf} {m_3+m_2+m_1}\] \[T_1\,=\,\frac{m_1m_3gf+3m_1m_2gf+m_1m_2g+m_1m_3g} {m_3+m_2+m_1}\] \[T_1\,=\,\frac{m_1g\left[m_3(f+1)+ m_2(3f+1)\right]} {m_3+m_2+m_1}\tag{14}\]Calculation of tensile force T2:
We express the force T2 from equation (11):
\[T_2\,=\,m_2a\,+\,m_2gf\,=\,m_2\frac{m_1g-m_3gf-3m_2gf} {m_3+m_2+m_1}\,+\,m_2gf\]We convert it to the last common denominator:
\[T_2\,=\,\frac{m_1m_2g-m_2m_3gf-3m_2^2gf+m_1m_2gf+m_2^2gf+m_2m_3gf} {m_3+m_2+m_1}\] \[T_2\,=\,\frac{m_1m_2g-2m_2^2gf+m_1m_2gf} {m_3+m_2+m_1}\] \[T_2\,=\,\frac{m_2g\left[m_1(1+f)-2m_2f\right]} {m_3+m_2+m_1}\tag{15}\]ANSWER
The value of acceleration of the cubes is: \[a\,=\,\frac{g\left(m_1-m_3f-3m_2f\right)}{m_3+m_2+m_1}.\]
The value of the tensile force stretching the fibre between the cubes m2 and m3 is
\[T_1\,=\,\frac{m_1g\left[m_3\left(f+1\right)+ m_2\left(3f+1\right)\right]}{m_3+m_2+m_1}\,.\]The value of the tensile force stretching the fibre between the cubes m3 and m1 is
\[T_2\,=\,\frac{m_2g\left[m_1\left(1+f\right)-2m_2f\right]}{m_3+m_2+m_1}\,.\]



