A ladybug crawling on a rotating cylinder

Task number: 385

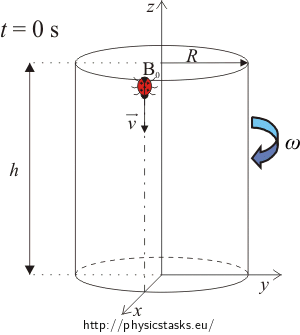
A cylinder with radius R and height h turns at constant speed clockwise around its own axis. The cylinder makes one turn per time T. There is a ladybug creeping along the surface of the cylinder. The speed of the ladybug v is constant and downward (in the axial direction) with regard to the cylinder.

Determine the time dependent position vector of the ladybug with respect to its surroundings. Assume that it starts moving at time t = 0 s from the top of the cylinder.
Determine the velocity (magnitude) of the ladybug with respect to its surroundings (not to the cylinder).
Determine the magnitudes of both the tangent and the centripetal accelerations of the ladybug.
What is the name of the curve one could use to describe the trajectory of the ladybug? Determine the radius of curvature of this trajectory.
What is the distance the ladybug covered during its motion between the top and bottom surfaces of the cylinder?

Solve all tasks from the point of view of an observer standing next to the cylinder.

Let’s establish the system of coordinates so the axis z matches the axis of the cylinder and axes x and y are parts of the cylinder’s bottom.

Hint 1 (task a): a picture of the situation
Let’s establish the coordinate origin at the centre of the cylinder’s bottom and the ladybug’s starting point at the edge of the cylinder’s top.

Draw a picture capturing the situation at time t = 0 s and mark in it the ladybug’s position.

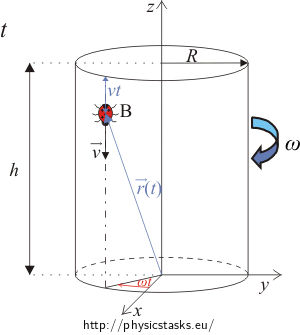
Then draw a picture capturing the situation at some random time t and in it the ladybug’s position.
Solution of hint 1
Picture 1:

Picture 2:
Hint 2 (task a): The time dependent position vector of the ladybug
Let’s split the motion in two; one motion in direction of the z axis and the second motion in the xy plane. What are these motions for?

Determine the time dependent coordinates x, y, z of the ladybug and after that, using these coordinates, determine its position vector.
Solution of hint 2
We split the ladybug’s motion into a uniform motion with speed v (in the direction of the z axis) and a circular motion with angular velocity \(\omega=\frac{2\pi}{T}\) (in the xy plane):
\[x(t)=R\cos\omega{t}=R\cos\frac{2\pi}{T}t\] \[y(t)=-R\sin\omega{t}=-R\sin\frac{2\pi}{T}t\] \[z(t)=h-vt\] \[\vec{r}(t)= x\vec{i}+ y\vec{j}+ z\vec{k}\] \[\vec{r}(t)= R\cos\left(\frac{2\pi}{T}t\right)\vec{i}-R\sin\left(\frac{2\pi}{T}t\right)\vec{j}+(h-vt)\vec{k}\]
where \(\vec{i}\), \(\vec{j}\), \(\vec{k}\) are the unit vectors codirectional with the x, y and z axes
Hint 3 (task b): Time dependent velocity of the ladybug
First find the components v_x, v_y, v_z of the velocity. To solve this problem you may use a parametric expression for the position.

Then find the magnitude of the time dependent velocity of the ladybug.
Solution of hint 3
The components of the beetle’s velocity can be found by taking time derivatives of the components of the position vector of the ladybug.

\[v_x=\frac{dx}{dt}= \frac{d}{dt}(R\cos\omega{t}= -R\omega\sin\omega{t}=-R\frac{2\pi}{T}\sin\frac{2\pi}{T}t \] \[v_y=\frac{dy}{dt}= \frac{d}{dt}(-R\sin\omega{t}= -R\omega\cos\omega{t}=-R\frac{2\pi}{T}\cos\frac{2\pi}{T}t \] \[v_z=\frac{dz}{dt} = \frac{d}{dt}(h-vt)= -v\]

The time dependent velocity of the ladybug is:

\[v_v=|\vec{v}(t)|=\sqrt{v_x^{2}+v_y^{2}+v_z^{2}}= \sqrt{R^{2}\omega^{2}(sin^{2}\omega{t}+ cos^{2}\omega{t})+ v^{2}}=\] \[ = \sqrt{v^{2}+R^{2}\omega^{2}} = \sqrt{v^{2}+R^{2}(\frac{2\pi}{T})^{2}}=\sqrt{4\pi^{2}\frac{R^{2}}{T^{2}}+v^{2}}\]
Hint 4 (task c): The magnitudes of both the tangential and centripetal accelerations of the beetle
If we know the velocity of the ladybug (if not see hint 3), we may easily calculate its tangential acceleration.

To find the magnitude of the normal (centripetal) acceleration we would need both the magnitude of the tangential acceleration and the magnitude of the total acceleration. The overall acceleration could be also (as in the case of velocity) calculated from its components a_x, a_y, a_z.

What is the relation between the total acceleration and its tangential and normal (centripetal) parts?
Solution of hint 4
Express the tangential acceleration a_t of the ladybug:

\[a_t(t)=\frac{dv_v}{dt} = \frac{d}{dt}\sqrt{v^{2}+R^{2}(\frac{2\pi}{T})^{2}} \] \[a_t=0\]

The relationship between the magnitudes of the tangential (a_t), normal (a_n) and overall (a) acceleration is:

\[a=\sqrt{a_t^{2}+ a_n^{2}}\] \[a_n=\sqrt{a^{2}-a_t^{2}}=a\]

We may now determine the components of the overall acceleration and then also its magnitude:

\[a_x(t)= \frac{dv_x}{dt}= \frac{d}{dt}(-R\omega\sin\omega{t}=-R\omega^{2}\cos\omega{t}=-R\frac{4\pi^{2}}{T^{2}}\cos\frac{2\pi}{T}t \] \[a_y(t)= \frac{dv_y}{dt}= \frac{d}{dt}(-R\omega\cos\omega{t}=R\omega^{2}\sin\omega{t}=R\frac{4\pi^{2}}{T^{2}}\sin\frac{2\pi}{T}t \] \[a_z(t)= \frac{dv_z}{dt}= \frac{d}{dt}(-v)=0\]

\[a=\sqrt{a_x^{2}+a_y^{2}+a_z^{2}}=\sqrt{R^{2}\omega^{4}\cos^{2}\omega{t}+R^{2}\omega^{4}\sin^{2}\omega{t}+0}=\] \[=R\omega^{2}=4R\frac{\pi^{2}}{T^{2}}\]

The time dependent normal acceleration a_n of the ladybug is then:

\[a_n = a =R\omega^{2}=4R\frac{\pi^{2}}{T^{2}}\]
Hint 5 (task d): The trajectory of the ladybug, the radius of curvature
First imagine the beetle’s trajectory in the case of its having zero velocity with respect to the rotating cylinder (i.e. the beetle is sitting on the rotating cylinder). Then add in the ladybug’s motion with respect to the cylinder. What is the curve swept out by its motion?

Remark: Realize that you must solve this problem from the point of view of an inertial reference frame, i.e. you watch the ladybug’s motion from a stationary reference frame next to the rotating cylinder.

What is the relation between the radius of curvature of its trajectory and both its velocity and centripetal acceleration?
Solution of hint 5
Trajectory of the motion::

The ladybug moves along a helix.

Remark: Finding the radius of curvature at some point of a curve means to fit the nearby points of the curve to a circle. The radius of such a circle is called the radius of curvature. For circular motion it is true that:
\[a_c=\frac{v^{2}}{R},\]
where a_c is the centripetal (normal) acceleration, v is the tangential velocity and R is the radius of the circle.

So, in our case:

The relation between the normal acceleration a_n, the velocity of the ladybug v_v and ρ (the radius of curvature) is:
\[a_n=\frac{v_v^{2}}{\rho}\]
The radius of curvature is then:
\[\rho=\frac{v_v^{2}}{a_n}\] \[\rho=\frac{R^{2}\omega^{2}+v^{2}}{R\omega^{2}}\]
where \(\omega=\frac{2\pi}{T}\)

and so: \[\rho=\frac{R^{2}\frac{4\pi^{2}}{T^{2}}+v^{2}}{R\frac{4\pi^{2}}{T^{2}}}=R+\frac{v^{2}T^{2}}{4\pi^{2}R}\]
Hint 6 (task e): the distance traveled by the ladybug
The distance traveled by the ladybug, i.e. the length of its trajectory, we may easily find using its velocity and the overall time of its motion. The overall time is the time in which it moves from the top to the bottom of the cylinder.
Solution of hint 6
The velocity of the ladybug (with respect to its surroundings) is constant and so the distance l could be expressed as:

\[l=v_vt\]
where \(v_v = \sqrt{(R^{2}\omega^{2}+v^{2})}\) and \(t=\frac{h}{v}\).
\[l=(\frac{h}{v})\sqrt{(R^{2}\omega^{2}+v^{2})},\]
where \(\omega=\frac{2\pi}{T}\).

And so: \[l=(\frac{h}{v})\sqrt{4\pi^{2}\frac{R^{2}}{T^{2}}+v^{2}}\]
Complete solution
Picture 1:

Picture 2:

a) We split the ladybug’s motion into a uniform motion with speed v (in the direction of the z axis) and a circular motion with angular velocity \(\omega=\frac{2\pi}{T}\) (in the xy plane):
\[x(t)=R\cos\omega{t}=R\cos\frac{2\pi}{T}t\] \[y(t)=-R\sin\omega{t}=-R\sin\frac{2\pi}{T}t\] \[z(t)=h-vt\] \[\vec{r}(t)= x\vec{i}+ y\vec{j}+ z\vec{k}\] \[\vec{r}(t)= R\cos\left(\frac{2\pi}{T}t\right)\vec{i}-R\sin\left(\frac{2\pi}{T}t\right)\vec{j}+(h-vt)\vec{k}\]
where \(\vec{i}\), \(\vec{j}\), \(\vec{k}\) are the unit vectors codirectional with the x, y and z axes

b) The components of the beetle’s velocity can be found by taking time derivatives of the components of the position vector of the ladybug.

\[v_x=\frac{dx}{dt}= \frac{d}{dt}(R\cos\omega{t}= -R\omega\sin\omega{t}=-R\frac{2\pi}{T}\sin\frac{2\pi}{T}t \] \[v_y=\frac{dy}{dt}= \frac{d}{dt}(-R\sin\omega{t}= -R\omega\cos\omega{t}=-R\frac{2\pi}{T}\cos\frac{2\pi}{T}t \] \[v_z=\frac{dz}{dt} = \frac{d}{dt}(h-vt)= -v\]

The time dependent velocity of the ladybug is:

\[v_v=|\vec{v}(t)|=\sqrt{v_x^{2}+v_y^{2}+v_z^{2}}= \sqrt{R^{2}\omega^{2}(sin^{2}\omega{t}+ cos^{2}\omega{t})+ v^{2}}=\] \[ = \sqrt{v^{2}+R^{2}\omega^{2}} = \sqrt{v^{2}+R^{2}(\frac{2\pi}{T})^{2}}=\sqrt{4\pi^{2}\frac{R^{2}}{T^{2}}+v^{2}}\]

c) Express the tangential acceleration a_t of the ladybug:

\[a_t(t)=\frac{dv_v}{dt} = \frac{d}{dt}\sqrt{v^{2}+R^{2}(\frac{2\pi}{T})^{2}} \] \[a_t=0\]

The relationship between the magnitudes of the tangential (a_t), normal (a_n) and overall (a) acceleration is:

\[a=\sqrt{a_t^{2}+ a_n^{2}}\] \[a_n=\sqrt{a^{2}-a_t^{2}}=a\]

We may now determine the components of the overall acceleration and then also its magnitude:

\[a_x(t)= \frac{dv_x}{dt}= \frac{d}{dt}(-R\omega\sin\omega{t}=-R\omega^{2}\cos\omega{t}=-R\frac{4\pi^{2}}{T^{2}}\cos\frac{2\pi}{T}t \] \[a_y(t)= \frac{dv_y}{dt}= \frac{d}{dt}(-R\omega\cos\omega{t}=R\omega^{2}\sin\omega{t}=R\frac{4\pi^{2}}{T^{2}}\sin\frac{2\pi}{T}t \] \[a_z(t)= \frac{dv_z}{dt}= \frac{d}{dt}(-v)=0\]

\[a=\sqrt{a_x^{2}+a_y^{2}+a_z^{2}}=\sqrt{R^{2}\omega^{4}\cos^{2}\omega{t}+R^{2}\omega^{4}\sin^{2}\omega{t}+0}=\] \[=R\omega^{2}=4R\frac{\pi^{2}}{T^{2}}\]

The time dependent normal acceleration a_n of the ladybug is then:

\[a_n = a =R\omega^{2}=4R\frac{\pi^{2}}{T^{2}}\]

d) Trajectory of the motion::

The ladybug moves along a helix.

Remark: Finding the radius of curvature at some point of a curve means to fit the nearby points of the curve to a circle. The radius of such a circle is called the radius of curvature. For circular motion it is true that:
\[a_c=\frac{v^{2}}{R},\]
where a_c is the centripetal (normal) acceleration, v is the tangential velocity and R is the radius of the circle.

So, in our case:

The relation between the normal acceleration a_n, the velocity of the ladybug v_v and ρ (the radius of curvature) is:
\[a_n=\frac{v_v^{2}}{\rho}\]
The radius of curvature is then:
\[\rho=\frac{v_v^{2}}{a_n}\] \[\rho=\frac{R^{2}\omega^{2}+v^{2}}{R\omega^{2}}\]
where \(\omega=\frac{2\pi}{T}\)

and so: \[\rho=\frac{R^{2}\frac{4\pi^{2}}{T^{2}}+v^{2}}{R\frac{4\pi^{2}}{T^{2}}}=R+\frac{v^{2}T^{2}}{4\pi^{2}R}\]

e) The velocity of the ladybug (with respect to its surroundings) is constant and so the distance l could be expressed as:

\[l=v_vt\]
where \(v_v = \sqrt{(R^{2}\omega^{2}+v^{2}})\) and \(t=\frac{h}{v}\).
\[l=(\frac{h}{v})\sqrt{(R^{2}\omega^{2}+v^{2})},\]
where \(\omega=\frac{2\pi}{T}\).

And so: \[l=(\frac{h}{v})\sqrt{4\pi^{2}\frac{R^{2}}{T^{2}}+v^{2}}\]
Answers
a) The time dependent position vector of the ladybug is:

\[\vec{r}(t)= R\cos\frac{2\pi}{T}t \vec{i}-R\sin\frac{2\pi}{T}t\vec{j}+(h-vt)\vec{k}\]
where \(\vec{i}\), \(\vec{j}\), \(\vec{k}\) are the unit vectors codirectional with the x, y and z axes.

b) The magnitude of the ladybug’s velocity is:

\[v_v=|\vec{v}(t)|=\sqrt{v^{2}+R^{2}\omega^{2}}=\sqrt{4\pi^{2}\frac{R^{2}}{T^{2}}+v^{2}}\]

c) The tangential acceleration of the ladybug is:

\[a_t=0\,\textrm{m}\cdot\textrm{s}^{-2}\]

And the magnitude of the normal acceleration a_n of the ladybug is:

\[a_n=\sqrt{a^{2}-a_t^{2}}=R\omega^{2}=4R\frac{\pi^{2}}{T^{2}}\]

Both the tangential and normal accelerations are constant, i.e. time independent.

d) The ladybug moves along a helix and its radius of curvature is:

\[\rho=\frac{R^{2}\omega^{2}+v^{2}}{R\omega^{2}}=R+\frac{v^{2}T^{2}}{4\pi^{2}R}\]

e) The distance l is:

\[l=(\frac{h}{v})\sqrt{4\pi^{2}\frac{R^{2}}{T^{2}}+v^{2}}\]