Centre of Gravity of a Semi-Circular Wire

Task number: 2231

Determine the position of the centre of gravity of a thin homogeneous wire of mass m bent into a semicircle of radius R.

Hint 1
Think about what it means to “determine the centre of gravity”. What will be the output of the problem and what are you actually determining?
Solution of Hint 1
Determination of the centre of gravity means finding its coordinates in some suitable coordinate system. Thus, three coordinates of the centre of gravity G: x_G, y_G, z_G, will be the output of the problem.
Hint 2
Draw an appropriate semicircle in a coordinate system. How can we place it there to make further calculations easier? (In other words, do we really have to determine x, y and z coordinate? Could we choose such a coordinate system in which some coordinates would be obvious?)
Solution of Hint 2
An example of a suitable choice of a coordinate system in which further calculation will take place is shown below:

Imagine putting a semi-circular wire on a horizontal table. When viewed from above, it looks like a semicircle (Fig. 1).

We aim the z-axis vertically upwards (pointing out of the screen).

We select the y-axis in a way so that it bisects the semicircle splitting it, when viewed from above, into two quarter circles.

The x-axis is perpendicular to both previous axes.

The thin wire lies in the xy plane, therefore, z-coordinate of the centre of gravity is zero:
\[z_G\,=\,0.\]
It is obvious from the figure that the x-coordinate of the centre of gravity is also zero:
\[x_G\,=\,0.\]
(The object is symmetric with respect to the y-axis, thus its centre of gravity has to lie on this axis.) So we just need to determine the y-coordinate of the centre of gravity.
Hint 3
What is the general formula for the position vector r_G of the centre of gravity?
Solution of Hint 3
Position vector r_G of the centre of gravity of an object can be determined from:
\[\vec{r}_G\,=\,\frac{\int{\vec{r}}dm}{{\int}dm}.\tag{1}\]
Hint 4
According to the task assignment, the wire is homogeneous. Use this fact to transform relation (1) so that it is expressed through the length elements instead of the mass elements.
Solution of Hint 4
Mass element dm of a homogeneous wire can be expressed as follows:

\[dm\,=\,{\rho}dl,\]

where ρ is the length density of the material and dl is the length element. Then it holds true that:
\[\vec{r}_G\,=\,\frac{{\rho}\int{\vec{r}}dl}{{\rho}{\int}dl}\,=\,\frac{\int{\vec{r}}dl}{{\int}dl}.\]
The term in the denominator represents the sum of all length elements that form the wire, so we obtain the total length of the wire l:
\[\vec{r}_G\,=\,\frac{\int{\vec{r}}dl}{l}.\tag{2}\]
Hint 5
What will change in relation (2) since we are determining only the y-coordinate of the centre of gravity y_G as we have mentioned before?
Solution of Hint 5
Since the coordinates of the position vector r_G in relation (1) and (2) are calculated separately, for the y-coordinate we can simply use:
\[y_G\,=\,\frac{\int{y}dl}{l}.\tag{3}\]
Hint 6
In the Cartesian coordinate system, further calculation based on relation (3) is rather inconvenient. Mark a short length element dl in the figure, the corresponding y-coordinate and angle φ measured from the x-axis in a counterclockwise direction. Express the Cartesian y-coordinate using the radius of the semicircle R and angle φ. Also, express the length element dl using the corresponding angle dφ and radius R (drawing the situation might be helpful).
Solution of Hint 6

For angle φ we get:
\[\sin{\varphi}\,=\frac{y}{R}\,\Rightarrow\,y\,=\,R\sin{\varphi}.\tag{5}\]
We can also see from Figure 2 that:
\[dl\,=\,Rd\varphi.\tag{4}\]
Substituting the expressed variables into relation (3), we obtain:
\[y_G\,=\,\frac{\int{R\sin{\varphi}Rd\varphi}}{l}.\]
We can also substitute the length of the semicircle l = πR:
\[y_G\,=\,\frac{\int{R^2\sin{\varphi}d\varphi}}{{\pi}R}\,=\,\frac{R}{\pi}\int{\sin{\varphi}d{\varphi}}.\tag{6}\]
Hint 7
Fill in the appropriate integration limits in integral (6) and calculate the y-coordinate of the centre of gravity.
Solution of Hint 7
Angle φ changes from φ = 0 to φ = π.
\[y_G\,=\,\frac{R}{\pi}\int_0^{\pi}{\sin{\varphi}d{\varphi}}\,=\,\frac{R}{\pi}[-\cos{\varphi}]_0^{\pi}\,=\,\frac{R}{\pi}(1-(-1))\,=\,\frac{2R}{\pi}\]
Thus, the last coordinate of the centre of gravity in our coordinate system is y_G = 2R/π.
Overall Solution
Determination of the centre of gravity means the determination of its coordinates in some suitable coordinate system. Thus, three coordinates of the centre of gravity G: x_G, y_G, z_G will be the output of the problem.

If we choose a suitable coordinate system wisely, we can obtain some coordinates of the centre of gravity without calculations. An example of an appropriate coordinate system (in which further calculation will take place) is as follows:

Imagine putting a semi-circular wire on a horizontal table. When viewed from above, it looks like a semicircle (Fig. 1).

We aim the z-axis vertically upwards (pointing out of the screen).

We select the y-axis in a way so that it bisects the semicircle, splitting it, when viewed from above, into two quarter circles.

The x-axis is perpendicular to both previous axes.

The thin wire lies in the xy-plane, therefore, the z-coordinate of the centre of gravity is zero:
\[z_G\,=\,0.\]
It is obvious from the figure that the x-coordinate of the centre of gravity is also zero:
\[x_G\,=\,0.\]
(The object is symmetric with respect to the y-axis, thus its centre of gravity has to lie on this axis.) So we just need to determine the y-coordinate of the centre of gravity.

Position vector r_G of the centre of gravity of an object can be determined from:
\[\vec{r}_G\,=\,\frac{\int{\vec{r}}dm}{{\int}dm}.\tag{1}\]
Mass element dm of a homogeneous wire can be expressed as follows:

\[dm\,=\,{\rho}dl,\]

where ρ is the length density of the material and dlis the length element. Then it holds true that:
\[\vec{r}_G\,=\,\frac{{\rho}\int{\vec{r}}dl}{{\rho}{\int}dl}\,=\,\frac{\int{\vec{r}}dl}{{\int}dl}.\]
The term in the denominator represents the sum of all length elements that form the wire, so we obtain the total length of the wire l:
\[\vec{r}_G\,=\,\frac{\int{\vec{r}}dl}{l}.\tag{2}\]
Since the coordinates of the position vector r_G in relation (1) and (2) are calculated separately, for the y-coordinate we can simply use:
\[y_G\,=\,\frac{\int{y}dl}{l}.\tag{3}\]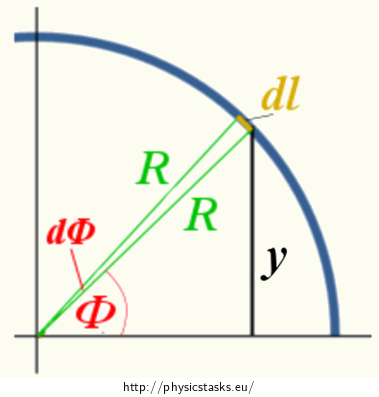

Now we transform our cartesian coordinates into polar coordinates. For angle φ we get:
\[\sin{\varphi}\,=\frac{y}{R}\,\Rightarrow\,y\,=\,R\sin{\varphi}.\tag{5}\]
We can also see from Figure 2 that:
\[dl\,=\,Rd\varphi.\tag{4}\]
Substituting the expressed variables into relation (3), we obtain:
\[y_G\,=\,\frac{\int{R\sin{\varphi}Rd\varphi}}{l}.\]
We can also substitute the length of the semicircle l = πR:
\[y_G\,=\,\frac{\int{R^2\sin{\varphi}d\varphi}}{{\pi}R}\,=\,\frac{R}{\pi}\int{\sin{\varphi}d{\varphi}}.\tag{6}\]
Then we set the limits of the integral for angle φ. It varies from φ = 0 to φ = π.
\[y_G\,=\,\frac{R}{\pi}\int_0^{\pi}{\sin{\varphi}d{\varphi}}\,=\,\frac{R}{\pi}[-\cos{\varphi}]_0^{\pi}\,=\,\frac{R}{\pi}(1-(-1))\,=\,\frac{2R}{\pi}\]
Thus, the last coordinate of the centre of gravity in our coordinate system is y_G = 2R/π; other coordinates are equal to zero.
Answer
Coordinates of the centre of gravity in our chosen coordinate system are as follows:
\[x_G\,=\,0,\] \[y_G\,=\,\frac{2R}{\pi},\] \[z_G\,=\,0.\]