A pair of weights on the pulley
Task number: 656
A fibre (with weights of mass m1 and m2 (m2 > m1) hanging on both its ends) is extended over a pulley. We suppose that the fibre is nonmaterial and the pulley is a homogenous cylinder with radius r and mass m3. Find the acceleration of weights.
The moment of inertia of a cylinder
The moment of inertia of the cylinder rotating about the axis of symmetry given by the table is \(I=\frac{1}{2}mr^2\).
Analysis
It is possible to solve this task in two ways: either by the law of conservation of mechanical energy (Hint marked as A) or the Impulse-momentum theorem (Hint marked as B). In the first case it is necessary to choose two appropriate situations in which you will compare the mechanical energy of the pulley and both weights with each other.
When solving the problem by the Impulse-momentum theorem it is necessary to consider which forces affect the pulley and the two weights and what holds for the resultant moment of the forces. It is also necessary to write the Angular momentum theorem for the rotation of the pulley.
(Impulse-momentum theorem and Angular momentum theorem see the task A rolling hoop.)
Hint 1A
Choose two situations in which you will compare the mechanical energy of the pulley and the two weights with each other. Don’t forget to choose the zero level of potential energy.
Hint 2A
Express both potential and kinetic energy of both weights and the pulley in situations 1 and 2. Substitute into the equation (1).Tricky question 3A
The speed figures in expressions for the kinetic energy. Express it by the acceleration and the covered distance h.
Hint 1B
Draw all forces (which act on the two weights and the pulley) into the picture.
Hint 2B
Write what holds for the resultant of forces affecting both individual weights and the pulley. Write the Angular momentum theorem for the pulley.
Hint 3B
Express from equations (3), (4), (5) the sought acceleration.
Answer
The magnitude of acceleration of the weights is \(a=\frac{(m_2-m_1)g}{m_1+m_2+\frac{1}{2}m_3}.\)
Complete solution with help of the law of conservation of mechanical energy
Choose two situations in which you will compare the mechanical energy of the pulley and the two weights with each other. Choose the zero level of potential energy.
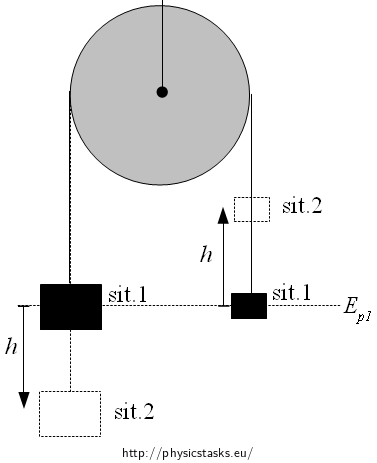
In the first situation we place the weights so that their centres of gravity are at the same height which we use as the zero level of potential energy.
We compare the mechanical energy Ep1, Ek1 of both weights and the pulley at the beginning (in the picture see as sit. 1) and after the covered distance h: Ep2, Ek2 ((in the picture see as sit.2).
The following holds true according to the law of conservation of mechanical energy:
\[E_{p1}+E_{k1} = E_{p2}+E_{k2}\tag{1}\]At the beginning the coordinates system doesn’t move therefore it is given:
\[E_{k1}=0.\]Similarly, the potential energy of the two weights equals zero. The only part of the system, which stands out of the zero level, is the pulley – we mark its potential energy as Eppulley.
\[E_{p1}=E_{ppulley}\]Potential energy of the heavier weight diminishes and equals -m2gh in situation 2. On the contrary potential energy of the lighter weight increases and equals m1gh in situation 2. Potential energy of the pulley doesn’t change. The total of the potential energy in situation 2 equals:
\[E_{p2}=(m_2-m_1)gh+E_{ppulley}\]Kinetic energy of the weight equals the sum of kinetic energies of both weights \(E_{kw}=\frac{1}{2}m_1v^2+\frac{1}{2}m_2v^2=\frac{1}{2}(m_1+m_2)v^2\) and kinetic energy of the rotating pulley \(E_{rot}=\frac{1}{2}I\omega^2\).
The peripheral speed of the pulley equals the speed of the motion of the weights and therefore: \(\omega=\frac{v}{r}\).
The moment of inertia of the pulley \(I=\frac{1}{2}m_3r^2\).
We substitute:
\[E_{rot}=\frac{1}{2}(\frac{1}{2}m_3r^2)(\frac{v}{r})^2=\frac{1}{4}m_3v^2.\]The total kinetic energy of the system in situation 2 equals:
\[E_{k2} = \frac{1}{2}(m_1+m_2)v^2 + \frac{1}{4}m_3v^2\]After the substitution into the equation (1) we get:
\[E_{ppulley} = (m_1-m_2)gh+E_{ppulley} + \frac{1}{2}(m_1+m_2)v^2 + \] \[+ \frac{1}{4}m_3v^2\]We adjust:
\[(m_2-m_1)gh = \frac{1}{2}(m_1+m_2 + \frac{1}{2}m_3)v^2 \tag{2}\]The speed figures in expressions for the kinetic energy. Express it by the acceleration and the covered distance h.
Weights move with the constant acceleration. The following holds for the covered distance h:
\[h=\frac{1}{2}at^2\]The following holds for the speed:
\[v=at\]And so:
\[h=\frac{v^2}{2a}\]Where:
\[v^2 = 2ah\]We substitute into the equation (2):
\[(m_2-m_1)gh = \frac{1}{2}(m_1+m_2 + \frac{1}{2}m_3)2ah\]We divide by h:
\[(m_2-m_1)g = (m_1+m_2 + \frac{1}{2}m_3)a\]We express a:
\[a=\frac{(m_2-m_1)g}{m_1+m_2+\frac{1}{2}m_3}\]Complete solution with help of Impulse-momentum theorem
Draw all forces (which act on the two weights and the pulley) into the picture.
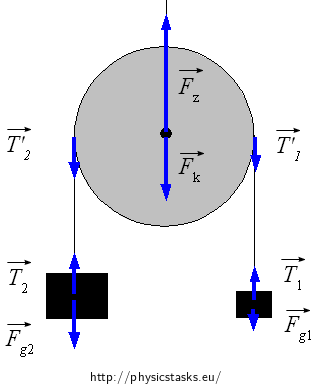
The gravitational forces \(\vec{F}_{g1}\), \(\vec{F}_{g2}\) and tension forces \(\vec{T_1}\), \(\vec{T_2}\) affect the weights. \(\vec{T_1}\) and \(\vec{T_2}\) affect the pulley, due to Newton`s third law, with equally strong forces \(\vec{T_1^,}\) and \(\vec{T_2^,}\) oriented in opposite directions.
Other forces that affect the pulley are gravitational force \(\vec{F}_k\) and force \(\vec{F}_z\), force \(\vec{F}_z\) is a force which the hanger of the pulley affects the pulley with to prevent the pulley from falling down.
The following holds for the resultant of forces:
The weight 1:
\[\vec{F}_{g1} + \vec{T}_1= m_1\vec{a}\]Scalar form (the coordinates system is given so that the upward direction is positive):
\[T_1 - F_{g1} = m_1a \tag{3}\]The weight 2:
\[\vec{F}_{g2} + \vec{T}_2= m_2\vec{a}\]Scalar form:
\[T_2 - F_{g2} = -m_2a\] \[- T_2 + F_{g2} = m_2a \tag{4}\]The pulley:
\[\vec{F}_{k} + \vec{F}_{z} + \vec{T^,}_{1}+ \vec{T^,}_{2} = 0\]Scalar form:
\[-F_{k} + F_{z} - T_{1}^, - T_{2}^, = 0\]The following holds for the resultant of the moment of inertia acting on the pulley about the axis of the centre of the mass:
\[\vec{r} \times \vec{T^,}_{1}+ \vec{r} \times \vec{T^,}_{2} = I\vec{\epsilon}\]Scalar form:
(We consider the clockwise rotation as negative.)
\[r T_{2}^, - r T_{1}^, = I\epsilon\]Substitute into \(I=\frac{1}{2}m_3r^2\), \(\epsilon = \frac{a}{r}\), \(T_{1}^,=T_{1}\), \(T_{2}^,=T_{2}\):
\[r T_{2} - r T_{1} = (\frac{1}{2}m_3r^2)\frac{a}{r}\] \[T_{2} - T_{1} = \frac{1}{2}m_3a\tag{5}\]Express from equations (3), (4), (5) the sought acceleration.
\[T_1 - F_{g1} = m_1a \tag{3}\] \[- T_2 + F_{g2} = m_2a \tag{4}\] \[T_{2} - T_{1} = \frac{1}{2}m_3a\tag{5}\]We adjust by adding the equation (3), (4) and (5) and we get:
\[F_{g2}-F_{g1}=m_1a+m_2a+\frac{1}{2}m_3a\] \[a=\frac{F_{g2}-F_{g1}}{m_1+m_2+\frac{1}{2}m_3}\] \[a=\frac{g(m_2-m_1)}{m_1+m_2+\frac{1}{2}m_3}\]



