Spring Scale on the Pole and on the Equator

Task number: 930

We calibrated a spring scale on the North Pole and then we moved the scale to the Equator.

Does the spring scale give the same readings as on the pole? Give reasons.

Hint 1 - Principle of operation of the spring scale
What is the principle of the operation of the spring scale? What physical quantity does it actually measure?
Solution of Hint 1
The spring scale uses elastic deformation of a spring to assess the mass of an object. Hooke’s law states that the relative extension of the spring is directly proportional to the force that the hanging object exerts on the spring. This force is called weight. The spring scale thus measures the weight of an object by the elongation of a spring.
Hint 2 - What is the weight comprised of?
The weight of an object arises from (and its magnitude is affected by) two other forces. What are these two forces? In what directions do they act?
Solution of Hint 2
Our problem is solved in the non-inertial reference frame of the Earth that rotates around its axis with angular velocity \(\omega\). The weight \(\vec{W}\) is thus a composition (vector addition) of:

a) the true gravity \(\vec{F}_{grav}\) with which the Earth attracts the object towards its center,

b) the centrifugal force \(\vec{F}_{cf}\) that appears to act on the object because it rotates together with the Earth; it acts perpendicular to the axis of rotation. The centrifugal force belongs to inertial or ‘fictitious’ forces - we cannot find who or what body is its originator.

Altogether: \[\vec{W}=\vec{F}_{grav}+\vec{F}_{cf}.\]
Hint 3 - Gravity and centrifugal force
We already know that the magnitude of the weight (often denoted simply as scalarW) depends on the magnitude of the true gravity and on the magnitude of the centrifugal force.

Is the magnitude of the true gravity (acting on a given object) the same everywhere on the surface of the Earth? If not so, where is it the greatest and where is it the smallest?

Is the magnitude of the centrifugal force (acting on a given object) the same everywhere on the surface of the Earth? If not so, where is it the greatest one and where is it the smallest one?
Solution of Hint 3
True gravity:

The magnitude of the true gravity at the surface of the Earth is given by Newton’s law of universal gravitation:
\[F_{grav}=G\frac{m\,M_E}{R_E^2},\]
where G is the gravitational constant, m is the mass of the object, \(M_E\) is the Earth mass and \(R_E\) is the distance between the object and the Earth’s center - the Earth radius in this case. This means that magnitude of this force is the same everywhere on the surface of the Earth (if we suppose that the Earth is a sphere).

Centrifugal force:

Every point on the surface of the Earth (except the poles) is moving with respect to the axis of the Earth on a circle. The magnitude of the centrifugal force is given by the formula:
\[F_{cf}=m{\omega^2}r=m\left(\frac{2\pi}{T}\right)^{2}r,\]
where m is the mass of the object, \(\omega\) is the angular velocity of rotation, T is the period of one turn of the Earth around its axis and r is the radius of the circle on which the given point revolves. It is obvious that the points on the Equator revolve on a circle with the largest radius - the full radius of the Earth - and must experience the largest centrifugal force. Points with larger latitudes revolve on circles with smaller ridii and experience weaker centrifugal forces and finally, there acts zero centrifugal force on the poles.
Hint 4
What follows from the previous hints regarding the magnitude of the weight on the poles and on the Equator (and also regarding the readings measured by the spring scale there)? Where does the spring scale indicate a larger weigth?
Solution of Hint 4
On the Pole, where r = 0, there is zero centrifugal force, and the weigth is equal to the gravity both in direction and in magnitude there:
\[\vec{W}_{Pole}=\vec{F}_{grav}\] \[W_{Pole}=F_{grav}\]
On the Equator, there is a maximum centrifugal force that acts in the opposite direction than the gravity (see the Figure in the complete solution below):
\[\vec{W}_{Eq}=\vec{F}_{grav}+\vec{F}_{cf}\] \[W_{Eq}=F_{grav}-F_{cf}\]
The spring scale indicates a lower reading on the Equator than on the Pole because it measures the total weight, not only the true gravity.
Complete solution
The spring scale measures the weight \(\vec{W}\) - the force that the object acts on the spring in the reference frame of the scale.

The scale and the object are both located in the non-inertial reference frame of the Earth that is rotating around its axis with the angular velocity \(\omega\). The weight is composed of:

1) the true gravity \(\vec{F}_{grav}\) acting between the Earth and the object - this force points towards the Earth center and its magnitude is the same everywhere on the surface of the Earth, according to Newton’s law of universal gravitation:
\[F_{grav}=G\frac{m\,M_E}{R_E^2}\,,\]
where G is the gravitational constant, m is the mass of the object, \(M_E\) is the Earth mass and \(R_E\) is the distance between the object and the Earth’s center - the Earth radius (we suppose that the Earth is a sphere).

2) the centrifugal force \(\vec{F}_{cf}\) that arises due to the rotation of the Earth around its axis (it is an inertial or fictitious force, one cannot find who or what body is its originator). Its vector lies in the plane perpendicular to the axis of the rotation (the Earth axis) and its magnitude depends on the position on the surface of the Earth according to the formula:
\[F_{cf}=m{\omega^2}r=m\left(\frac{2\pi}{T}\right)^{2}r,\]
where m is the mass of the object, \(\omega\) is the angular velocity of rotation, T is the period of one turn of the Earth around its axis and r is the radius of the circle on which the given point revolves with respect to the axis of rotation (it is the full Earth radius at the Equator only).

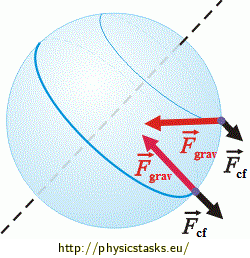
Together: \[\vec{W}=\vec{F}_{grav}+\vec{F}_{cf}\]

On the Pole, there is r = 0 and the centrifugal force is zero. The weight is then identical to the true gravitational force as for both the direction and the magnitude:
\[\vec{W}_{Pole}=\vec{F}_{grav}\] \[W_{Pole}=F_{grav}\]
On the Equator, there is a maximum centrifugal force that aims in the opposite direction than the true gravity (see the Figure):
\[\vec{W}_{Eq}=\vec{F}_{grav}+\vec{F}_{cf}\] \[W_{Eq}=F_{grav}-F_{cf}\]
Since the spring scale measures the weight, it indicates a smaller mass on the Equator than on the (North) Pole.

For an object with a mass of 1 kg:
\[M_E=5.98{\cdot}10^{24}\,\mathrm{kg}\] \[R_E=6.378{\cdot}10^{6}\,\mathrm{m}\] \[G=6.67{\cdot}10^{-11}\,\mathrm{N\cdot{m^2}\cdot{kg^{-2}}}\] \[T=24\,\mathrm{h}=86400\,\mathrm{s}\]
\[W_{Pole}=G\frac{m\,M_E}{R_E^2} = \left\{ 6.67{\cdot}10^{-11}\cdot\frac{1{\cdot}5.98{\cdot}10^{24}}{(6.378{\cdot}10^6)^2}\right\}\,\mathrm{N}\,\dot{=}\,9.805\,\mathrm{N}\]

\[\begin{align}W_{Eq} &=G\frac{m\,M_E}{R_E^2}-m\left(\frac{2\pi}{T}\right)^{2}R_E=\\ &=\left\{6.67{\cdot}10^{-11}\cdot\frac{1{\cdot}5.98{\cdot}10^{24}}{(6.378{\cdot}10^6)^2}-1\cdot\left(\frac{2\pi}{86400}\right)^2\cdot{6.378{\cdot}10^6}\right\}\,\mathrm{N}\,\dot{=}\\\\&\,\dot{=}\,\left(9.8052-0.0337\right)\,\mathrm{N} \,\dot{=}\, 9.772\,\mathrm{N}\end{align}\]
Answer
The spring scale indicates a smaller weight on the Equator than on the Pole when weighing the same object.
The actual reading on the Equator
A spring scale that was calibrated on the Pole indicates a mass of 1 kg when its spring is elongated by a force of 9.805 N - the weight of a 1–kg–object on the Pole.

The same object elongates the spring of the scale by a force of 9.771 N on the Equator and the Pole–calibrated scale thus indicates a mass of 9.772/9.805 = 0.997 kg here.
Hyperlink to a similar task
Centrifugal Force on the Equator