A Pendulum on a Merry-go-round
Task number: 1753
There is a weight of mass of 0.5 kg hung on a merry-go-round via a 1 m long string at distance 2 m from the axis of rotation. The weight is deviated from its resting position by 10°. What is the rotation period of the merry-go-round?
Solve this problem with respect to both an inertial frame of reference and a non-inertial frame of reference.
Notation
r = 2 m distance from the axis of rotation to where the string is attached to the merry-go-round l = 1 m length of the string α = 10° angle between the pendulum and its resting position m = 0,5 kg mass of the weight T = ? (s) rotation period of the merry-go-round From the Physics Reference Tables: g = 9.81 m·s−2 gravitational acceleration Hint 1: Drawing a Picture with Respect to an Inertial and a Non-Inertial Frame of Reference
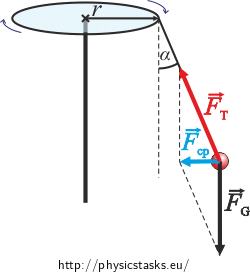
Draw two pictures. In one picture, include all the forces that act upon the weight as seen by an inertial observer standing next to the merry-go-round.
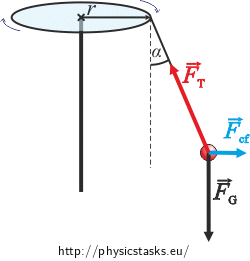
In the second picture, include all the forces that act upon the weight as seen by a non-inertial observer riding the merry-go-round.
Are there any differences between how the two observers see the situation? What motion does the weight perform relative the each of the observers? Are the forces acting upon the weight the same in the two situations? Is there the same amount of forces in the two situations?
Hint 2: Equation of Motion with Respect to an Inertial Observer
Summarize in a vector equation what holds for the forces acting upon the body with respect to an inertial observer.
Choose a coordinate system and write the equation in scalar form. Evaluate the desired rotation period.
Hint 3: Equation of Motion with Respect to a Non-Inertial Observer
Summarize in a vector equation what holds for the forces acting upon the body with respect to a non-inertial observer..
What does the net force equal to if the weight is at rest relative to the observer?
Choose a coordinate system and write the equation in scalar form. Evaluate the desired rotation period.
Answer
For both the inertial and the non-inertial system we get:
\[ T = 2\pi \sqrt{\frac{r + l\sin\alpha}{g \tan{\alpha}}}.\]The rotation period of the pendulum is 7 s.
Complete Solution
a) Solution with respect to an inertial frame
The weight performs a uniform circular motion relative to the observer standing next to the merry-go-round.
What forces are acting upon the weight?
- The weight is being held by the string that acts upon the weight with a tension force \(\vec{F}_T\)
- There is also the force of gravity \(\vec{F}_G\)
Combining the two forces we get the centripetal force \(\vec{F}_{cp}\), which points toward the axis of rotation and causes the curvature of the motion.
For the net force it holds:
\[\vec{F}_{T} + \vec{F}_{G} = \vec{F}_{cp}= m\vec{a}_{n},\]where \(\vec{F}_T\) is the tension force of the string, \(\vec{F}_G\) is the gravitational force, \(\vec{F}_cp\) is their net force and \(\vec{a}_n\) is the centripetal acceleration.
We will write the vector equation in scalar form in the direction of the x and y axes (see the picture for orientation).
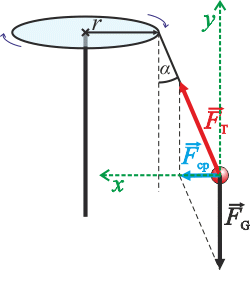
Horizontal direction (x axis):
\[{F}_{T} sin\alpha= m{a}_{n}.\]Vertical direction (y axis):
\[{F}_{T} cos\alpha = mg.\]If we evaluate FT rom the second equation and substitute it into the first we get:
\[mg \mathrm{tg}\alpha = m{a}_{n},\] \[g \mathrm{tg}\alpha = {a}_{n}.\]For a circular motion of radius ρ and using the conversion formulas for tangential and angular speed we get:
\[{a}_{n} = \frac{v^2}{\rho} = \omega^2\rho.\]We substitute:
\[g \mathrm{tg}\alpha = \omega^2\rho.\]Let us remember the relation between the angular speed ω and the rotation period T of a circular motion:
\[\omega = \frac{2\pi}{T}.\]Therefore:
\[g \mathrm{tg}\alpha = \frac{4\pi^2}{T^2} \rho.\]And so:
\[ T^2 = 4\pi^2\frac{\rho}{g \mathrm{tg}{\alpha}},\] \[ T = 2\pi \sqrt{\frac{\rho}{g \mathrm{tg}\alpha}}.\]The radius ρ, of the circular motion is given by the sum of the distance between the axis of rotation and the fixture of the string r and the distance rα caused by the deviation of the string of length l from its resting position by angle α.
It holds that:
\[\rho = r+r_\alpha = r + l\sin\alpha.\]Which gives us the final formula:
\[ T = 2\pi \sqrt{\frac{r + l\sin\alpha}{g \mathrm{tg}\alpha}}.\]Numerically:
\[ T = 2\pi \sqrt{\frac{2 + 1 sin10^{\circ}}{9.81 \mathrm{tg}10^{\circ}}}\,\mathrm{s} = 7\,\mathrm{s}.\]b) Solution with respect to a non-inertial frame
The weight is at rest relative to the observer riding the merry-go-round.
What forces are acting upon the weight?
Tension force of the string \(\vec{F}_T\)
Force of gravity \(\vec{F}_G\)
These two are real forces, we can find two partners that act upon each other (the rope – the weight; the Earth – the weight). If the net force is to be zero, we have to add a force that compensates the effects of the tension and the gravitational force: a centrifugal force \(\vec{F}_{cf}\) (we know what the force does but not who the other partner is).
As stated above, the weight is at rest relative to the observer riding the merry-go-round. The net force acting upon the body is equal to zero:
\[\sum{\vec{F}} = 0.\]We substitute the forces from the picture, i.e. the tensile force \(\vec{F}_T\), the force of gravity \(\vec{F}_G\) and the inertial centrifugal force \(\vec{F}_{cf}\). We get an equation in vector formi:
\[\vec{F}_T + \vec{F}_G + \vec{F}_{cf} = 0.\]We will write the vector equation in scalar form. We choose the coordinate system as shown in the picture.
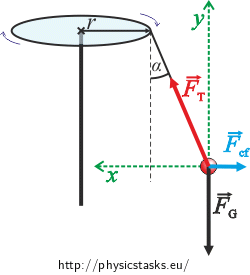
Horizontal direction (x axis):
\[{F}_T\sin\alpha = {F}_{od}.\]Vertical direction (y axis):
\[{F}_T\cos\alpha = mg,\]If we evaluate FT from the second equation and substitute it into the first we get:
\[mg \mathrm{tg}\alpha = {F}_{cf}.\]Let us remember the formula for an inertial centrifugal force acting during a circular motion of radius ρ depending on the angular speed ω and the relation between an angular speed and a rotation period T.
\[{F}_{cf} = m\omega^2\rho\] \[\omega = \frac{2\pi}{T}\]We substitute into the previous equation:
\[mg \mathrm{tg}\alpha = m\omega^2\rho,\] \[g \mathrm{tg}\alpha = \omega^2\rho,\] \[g \mathrm{tg}\alpha = \frac{4\pi^2}{T^2} \rho.\]We get:
\[ T^2 = 4\pi^2\frac{\rho}{g \mathrm{tg}{\alpha}},\] \[ T = 2\pi \sqrt{\frac{\rho}{g \mathrm{tg}{\alpha}}}.\]The radius ρ of the circular motion is given by the sum of the distance between the axis of rotation and the fixture of the string and the distance rα caused by the deviation of the string of length l from its resting position by angle α.
It holds that:
\[\rho = r+r_\alpha = r + l\sin\alpha.\]Which gives us the final formula:
\[ T = 2\pi \sqrt{\frac{r + l\sin\alpha}{g \mathrm{tg}{\alpha}}}.\]Numerically:
\[ T = 2\pi \sqrt{\frac{2 + 1 sin10^{\circ}}{9.81 \mathrm{tg}10^{\circ}}}\,\mathrm{s} = 7\,\mathrm{s}.\]