Pucks collision on the ice
Task number: 1517
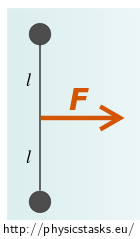
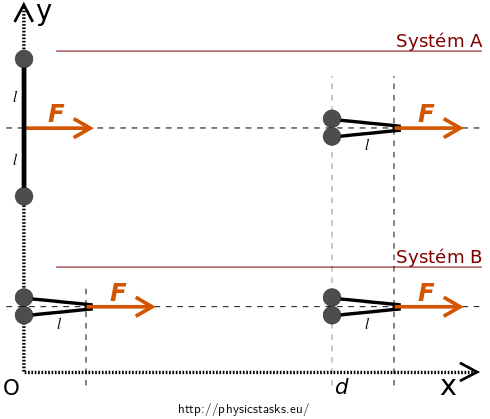
There are two pucks on the ice connected by fiber with insignificant mass and length \(2l\).
Constant force \(\vec{F}\) starts affecting the system and it is orthogonal to connecting line of pucks with point in the center of the connecting line.
Which part of mechanical energy transforms into internal energy during collision of the pucks?
Suppose that pucks move on ice without friction. Consider collision perfectly inelastic.
Analysis
Realize that puck are identical and their distances \(l\) from point of the force are the same. So system is symmetrical to vector line of the force \(\vec F\). So we can solve motion of only one puck and result extend on both of them in the end.
Tensile force \(\vec F\) affects both pucks trough the fiber, which we understand as mediator of the force (it doesn´t deform). When force starts acting, pucks move with acceleration in direction of vector of the force \(\vec{F}\) and direction of the connecting line as well. After some time pucks collide, considering symmetry of the task – on the vector line of the force \(\vec F\).
Kinetic energy from velocity in the direction of the collision right before it transforms into internal energy because of inelasticity of the collision. Pucks remain stuck together after the collision and their motion will continue in direction of the force \(\vec F\) only.
Kinetic energy of the pucks from velocity in direction of the force \(\vec{F}\) doesn´t change through the collision and keep rising because of permanent accelerating from the tensile force.
Pucks were still at the start. So some force has to accelerate them. Offenders are forces, which the pucks are drawn through fiber with. Constituent part of the force in direction of the connecting line belong to motion in this direction and its magnitude depends on angle between fibers in the moment. If we know the progress of this force, we can calculate gained and then lost kinetic energy as the work of this variable force when moving pucks from distance \(l\) to center of their connecting line.
Hint 1 – seeking of tensile forces
Draw a picture of situation few moments after force \(\vec F\) starts acting. Using parallelogram rule decompose force \(\vec F\) into directions of fibers.
Do you manage to find dependence magnitude of tensile forces on size of angle \(\vartheta\) between fiber and line of symmetry?
Hint 2 – establishment Oxy, tensile force decomposition
Establish coordinate system suitably and determine components of tensile force vector (e.g. \(\vec{T}_2\)).
Which component of force \(\vec{T}_2\) is responsible for accelerating of the system in the direction of \(\vec F\)? Which component of force \(\vec{T}_2\) is causing acceleration in the connecting line of the pucks?
Express component of the vector \(\vec{T}_2\) in the direction of \(y\) axis.
Hint 3 – “lost” energy calculation
Momentum of the system is preserved during perfectly inelastic collision. Examine momentum of the system before collision and after it.
Calculate kinetic energy of the motion of the puck in the direction of the \(y\) axis in the moment right before the collision.
How much energy transforms into internal energy during collision?
COMPLETE SOLUTION
There is situation of the system in some time between start of the motion and the collision in the right picture.
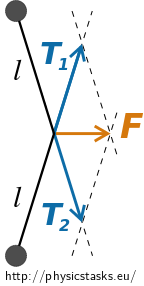
We decompose force \(\vec{F}\) into directions of the fibers using parallelogram rule on forces \(\vec{T}_1\) and \(\vec{T}_2\), i.e.
\[\vec{F} = \vec{T}_1 + \vec{T}_2.\]Examine following geometrical characteristic before we start finding dependence magnitude of tensile forces on size of angle between fibers and line of symmetry.
From symmetry given by fact that the force \(\vec F\) acts on fiber centrally perpendicular to the connecting line of the pucks follows that parallelogram of vectors is rhomboid and for magnitude of tensile forces stands
\[ |\vec{T}_1|=|\vec{T}_2| = T,\]It´s obvious that is enough solve problem for one puck and factor both pucks into result.
We turn to finding dependence magnitude of tensile force \(T\) on size of angle, which we denote \(\vartheta\) and is marked in the following picture.
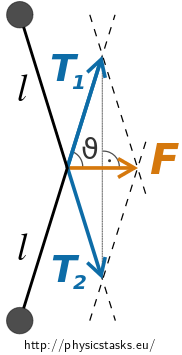
Because parallelogram of vectors is rhomboid (its diagonals halve each other) is valid
\[\cos \vartheta = \frac{|\vec{F}|/2}{T} = \frac{F}{2T}.\]We express dependence magnitude of tensile forces \(T\) on angle \(\vartheta\) from previous equation
\[ T = \frac{F}{2\cos\vartheta}. \tag{1}\]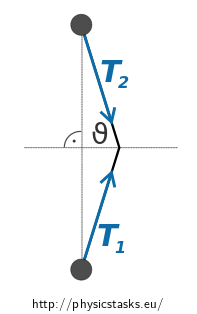
Tensile forces \(\vec{T}_1\) and \(\vec{T}_2\) acting on fibers, which fulfil function of rigid bond. Forces, which the pucks are pulled with, are represented equal vectors \(\vec{T}_1\) and \(\vec{T}_2\). We parallel move these vectors, with maintenance of orientation, so they’ve point in the center of the pucks for facilitation next considerations (see right fig.).
Magnitude of angle marked in the picture is equal to \(\vartheta\) from equation (1) based on geometrical characteristic. We’re using this during decomposition forces into marked direction.
Establish coordinate system \(\mathrm{Oxy}\) so \(x\) axis lies in the axis of the symmetry and is oriented in the direction of the vector \(\vec F\) and \(y\) axis is heading vertically. We identify origin with intersection of the connecting line of the pucks and symmetry axis.
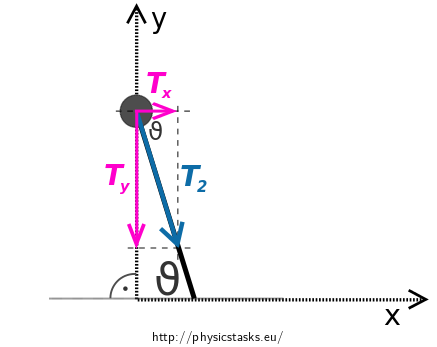
We decomposed force \(\vec{T}_2\) into components in the direction of the \(x\) axis (vector \(\vec{T}_x\)) and the \(y\) axis (vector \(\vec{T}_y\)).
- Force \(\vec{T}_x\) accelerates the puck in the direction of the \(x\) axis.
- Force \(\vec{T}_y\) accelerates the puck in the direction of the \(y\) axis.
Magnitude of both components of the force \(\vec{T}_2\) and instantaneous acceleration in both directions as well depends on the magnitude of angle \(\vartheta\).
For magnitudes of \(T_2\) and \(T_y\) stands
\[\sin \vartheta = \frac{T_y}{T_2} = \frac{T_y}{T}.\]For the component of the vector \(\vec{T}_2\) in the direction of the \(y\) axis using previous equation can be written
\[T_y = -T\sin\vartheta.\]Substituting expression (1) as T we gain
\[T_y = -\frac{F}{2\cos\vartheta}\sin\vartheta = -\frac{1}{2}F\,\mathrm{tg}\, \vartheta.\tag{2}\]Both pucks have the same mass and y-coordinates of their velocities are the same except for sign thanks to symmetry. Momentum and so velocity of the pair of the pucks in the direction of the \(y\) axis is null according to law of conservation of momentum.
Collision does not affect velocity of the pucks in the direction of the \(x\) axis, because impact takes place in the direction perpendicular to this axis. Velocity in this direction will grow still (with acceleration \(a = \frac{F}{2m}\)).
Kinetic energy of the motion of the puck in the direction of the \(y\) axis in the moment right before the collision is equal to work done by y-component of tensile force during moving the puck from point \([0;l]\) to the origin \([0;0]\). We’ll use integral calculus to calculate energy, because magnitude of \(T_y\) isn’t constant, it depends on angle \(\vartheta\) by equation (2).
\[E_{k(y)} = W_{\mathrm{l\to 0}} = \int_l^0 T_y(\vartheta)\,dy = \int_l^0 -\frac12 F \,\mathrm{tg}\, \vartheta \,dy.\]Because stands \(y = l\sin \vartheta\), (and differential \(\mathrm{d}y = l\cos\vartheta \,\mathrm{d}\vartheta\)) it’s possible to substitute and calculate integral (don’t forget recalculate limits).
\[ \int_l^0 -\frac12 F \,\mathrm{tg}\, \vartheta \,dy = -\frac12 Fl \int_{\frac{\pi}{2}}^0 \sin \vartheta \,d\vartheta = -\frac12 Fl\, \left[-\cos\vartheta\right]_{\pi/2}^0 = \frac12 Fl. \]Mechanical energy transformed into internal energy during collision of both pucks is twice as much as energy \(E_{k(y)}\), i.e.
\[E' = 2E_{k(y)} = Fl.\]Notation: Taks could be also solved without integral calculus
Except for arrangement we’re solving until now (system A) we consider arrangement B (system B), in which force \(\vec F\) starts acting on already “collided” pucks.
We let both systems A and B move in the direction of the \(x\) axis so all the pucks are on the \(y\) axis in the time of applying force \(\vec F\) in the mental experiment.
Answer
Into internal energy transforms kinetic energy of the pucks belongs to components of the velocities in the direction of the impact magnitude of \(E' = Fl\) during perfectly inelastic collision.