Elevator
Task number: 1982
The cabin of a fully loaded elevator has a mass of 1 200 kg. The cabin must be lifted to a height of 54 m in 3.0 min. The counterbalance has mass of only 950 kg, so the engine of the elevator must help in balancing the cabin. What is the average power of the tractive force of the motor acting upon the cabin through a tow rope?
Given values
M = 1 200 kg mass of the cabin m = 950 kg mass of the counterweight s = 54 m height to which the cabin must be lifted t = 3 min duration of lifting the cabin P = ? average power of the towing force of the engine Analysis
We will assume that the motion of the cabin of the elevator is uniform. First we will find out how big the towing force of the engine needs to be. Then we will calculate what work the towing force will do by lifting the cabin to the given height. Lastly we will determine the unknown power of the towing force.
Hint 1 – Acting forces
Draw a picture and mark the forces acting upon the cabin.
Assume the cabin of the elevator moves upwards uniformly. What holds for the total force acting upon it? With what force must the engine tow?
Hint 2 – Work and power
The tractive force of the engine is constant. What work will the engine do while lifting the cabin to a given height? What is the power of the engine?
Numerical solution
It is given:
\[M\,=\,1\,200\, \mathrm{kg}\] \[m\,=\,950\, \mathrm{kg}\] \[s\,=\,54\, \mathrm{m}\] \[t\,=\,3\, \mathrm{min}\,=\,180\, \mathrm{s}\] \[P\,=\,?\]From the tables:
\[g\,=\,9.81\, \mathrm{m \cdot s^{-2}}\]
\[P\,=\,\frac {\left(M-m\right)gs}{t}\] \[P\,=\,\frac{\left(1\,200\,-\,950\right)\cdot 9.81{\cdot}54}{180}\,\mathrm{W}\] \[P\,=\,735.75\, \mathrm{W}\,\dot=\,736\ \mathrm{W}\]Answer
The average power of the towing force of the engine is \[P\,=\,\frac {\left(M-m\right)gs}{t}\,\dot=\,736\ \mathrm{W}.\]
Celkové řešení
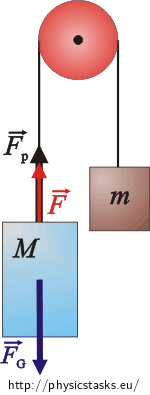
\(M\) … mass of the cabin
\(m\) … mass of the counterbalance
\(\vec F_{\mathrm{G}}\) … gravitational force acting upon the cabin \((F_\mathrm{G}\,=\,Mg)\)
\(\vec F_\mathrm{p}\) … towing force of the counterbalance \((F_\mathrm{p}\,=\,mg)\)
\(\vec F\) … towing force of the engine
In a uniform linear motion the acceleration and the total force acting upon the cabin is zero. It therefore holds that:
\[F_\mathrm{p}+F-F_{\mathrm{G}}\,=\,0\,.\]The towing force of the engine will be equal to
\[F\,=\,Mg-mg\,.\]Work performed by the towing force:
Work done by a constant force acting in the direction of the displacement s can be expressed with the relation:
\[W\,=\,Fs\,.\]We substitute for force F from relation (1):
\[W\,=\,\left(Mg-mg\right)s\,=\,\left(M-m\right)gs\,.\tag{2}\]Power of the towing force:
Power expresses how fast work is done:
\[P\,=\, \frac {W}{t}\,.\]We substitute for work from relation (2):
\[P\,=\,\frac {\left(M-m\right)gs}{t}\,.\] \[P\,=\,\frac{\left(1\,200\,-\,950\right)\cdot 9.81{\cdot}54}{180}\,\mathrm{W},\] \[P\,=\,735.75\, \mathrm{W}.\]Answer: The average power of the towing force is \(P\,=\,735.75\, \mathrm{W}.\)




