Ballistic pendulum 2
Task number: 279
A rifle bullet with a mass m = 4 g is horizontally fired with a speed v0 = 600 m s-1 into a ballistic pendulum with a mass M = 1 kg and a thickness d = 25 cm.
The bullet goes through the pendulum and leaves it with a speed of v1 = 100 m s-1. Find the magnitude of the constant force that slows down the bullet inside the pendulum and the vertical height through which the pendulum rises.
Note: The ballistic pendulum was used for measuring the speed of a bullet. It consists of a wooden block suspended from two long cords so that it can swing only in the vertical direction.
Analysis
Let us suppose that the bullet penetrates the block of the pendulum very fast and we do not consider any deviation from its original direction. We use the conservation laws of momentum (CLM) and energy (CLE).
Hint 1 – CLM
Draw a figure and write down the CLM for the system composed of the bullet and the pendulum.
Hint 2 – CLE
Write down the CLE for the system composed of the bullet and the pendulum. Compare the energies of the system immediately before the bullet embedded into the pendulum and immediately after the bullet left it.
Hint 3 – CLE for the pendulum
Write down the CLE for the pendulum at the moment the bullet left it and at the moment the pendulum reached the highest point through which it rises.
Solution of Hint 3 – CLE for the pendulum
The kinetic energy of the pendulum at the moment the bullet left it is changed into the potential energy:
\[E_k=E_p\]where \(E_k\) is the kinetic energy of the pendulum at the moment the bullet left it
and \(E_p\) is the potential energy of the pendulum at the highest point. Hence:
\[\frac{1}{2}Mv^2=Mgh\tag{5}\]where \(g\) denotes the acceleration of gravity.
Hint 4 - the force that slows down the bullet inside the pendulum and the vertical height through wh
Use the equations (1), (4) and (5) to express the force that slows down the bullet (the kinetic friction force) and the height through which the pendulum rises.
Numerical values
It is given:
\[m=4\,\mathrm{g}=0.004\, \mathrm{kg}\] \[v_0=600\,\mathrm{m s^{-1}}\] \[v_1=100\,\mathrm{m s^{-1}}\] \[g=9.81\,\mathrm{m s^{-2}}\] \[d=25\,\mathrm{cm}=0.25\,\mathrm{m}\] \[M=1\,\mathrm{kg}\]We are looking for:
\[h=?\] \[F=?\] \[h=\frac {m^2(v_0-v_1)^2}{2gM^2}\] \[h=\frac {0.004^2\cdot(600-100)^2}{2{\cdot}9.81{\cdot}1^2}\,\mathrm{m}\] \[h=0.2\, \mathrm{m}\] \[F=\frac {m}{2d}[v_0^2-v_1^2-\frac {m}{M}(v_0-v_1)^2]\] \[F=\frac {0.004}{2{\cdot}0.25}[600^2-100^2-\frac {0.004}{1}(600-100)^2]\, \mathrm{N}\] \[F=2792\,\mathrm{N}\,\dot=2.8\ \mathrm{kN}\]Answer
The pendulum rises into the vertical height \[h=\frac {m^2(v_0-v_1)^2}{2gM^2}=0.2\,\mathrm{m}\] .
The force that slows down the bullet inside the pendulum is \[F=\frac {m}{2d}[v_0^2-v_1^2-\frac {m}{M}(v_0-v_1)^2]=2792\,\mathrm{N}\,\dot=2.8\ \mathrm{kN}\] .
Complete solution
Let us suppose that the bullet penetrates the block of the pendulum very fast and we do not consider any deviation from its original direction. We use the conservation laws of momentum (CLM) and energy (CLE).
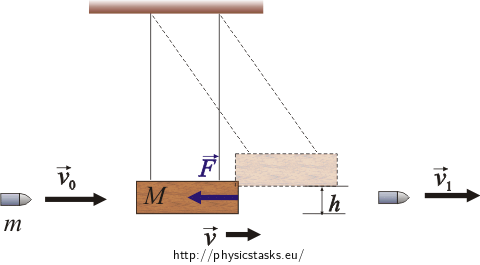
\(\vec{F}\)....... the constant force that slows down the bullet inside the pendulum
\(h\)....... the vertical height through which the pendulum rises
\(m\)....... the mass of the bullet
\(M\)...... the mass of the pendulum
\(\vec{v_0}\)..... the initial velocity of the bullet
\(\vec{v_1}\)..... the velocity of the bullet after leaving the pendulum
\(\vec{v}\)..... the velocity of the pendulum after the bullet left it
\[CLM :\qquad \vec{p_s}+\vec{p_k}=\vec{p_s^{'}}+\vec{p_k^{'}}\]\(\vec{p_s}\)..... the momentum of the bullet before embedding into the pendulum
\(\vec{p_k}\)..... the momentum of the pendulum before the bullet embedded into it
\(\vec{p_s^{'}}\)..... the momentum of the bullet immediately after leaving the pendulum
\(\vec{p_k^{'}}\)..... the momentum of the pendulum immediately after the bullet left it
\[m\vec{v_0}+0=m\vec{v_1}+M\vec{v}\]The velocities are parallel thus we can write the equation as for scalar quantities:
\[mv_0=mv_1+Mv\tag{1}\]At the moment the bullet embedded into the pendulum a part of the kinetic energy is transformed into the internal energy of the pendulum and the bullet, a part into the kinetic energy of the bullet after the penetration and a part into the kinetic energy of the pendulum:
\[CLE:\qquad\frac{1}{2}mv_0^2=\frac{1}{2}mv_1^2+\frac{1}{2}Mv^2+\Delta U\tag{2}\]where \(\Delta U\) is the change of the internal energy.
The change of the internal energy equals to the work done by the force that slows down the bullet F along the path d:
\[\Delta U=Fd\tag{3}\]where \(d\) is the thickness of the pendulum
We insert the expression (3) into the equation (2):
\[\frac{1}{2}mv_0^2=\frac{1}{2}mv_1^2+\frac{1}{2}Mv^2+Fd\tag{4}\]The kinetic energy of the pendulum at the moment the bullet left it is changed into the potential energy:
\[E_k=E_p\]where \(E_k\) is the kinetic energy of the pendulum at the moment the bullet left it
and \(E_p\) is the potential energy of the pendulum at the highest point. Hence:
\[\frac{1}{2}Mv^2=Mgh\tag{5}\]where \(g\) denotes the acceleration of gravity.
Let us express the speed of the pendulum from the equation (1):
\[mv_0=mv_1+Mv\tag{1}\] \[v=\frac{m(v_0-v_1)}{M}\tag{6}\]We insert it into (5):
\[\frac{1}{2}Mv^2=Mgh\] \[\frac{1}{2}M\frac{m^2(v_0-v_1)^2}{M^2}=Mgh\]and express the vertical height h through which the pendulum rises as:
\[h=\frac{m^2(v_0-v_1)^2}{2M^2g}\] \[h=\frac {0.004^2\cdot(600-100)^2}{2{\cdot}9.81{\cdot}1^2}\,\mathrm{m}\] \[h=0.2\, \mathrm{m}\]We derive the force that slows down the bullet from (4):
\[\frac{1}{2}mv_0^2=\frac{1}{2}mv_1^2+\frac{1}{2}Mv^2+Fd\tag{4}\] \[F=\frac{1}{2d}mv_0^2-\frac{1}{2d}mv_1^2-\frac{1}{2d}Mv^2\tag{4}\]Finally, we insert the speed v from (6) into the last equation:
\[F=\frac{1}{2d}mv_0^2-\frac{1}{2d}mv_1^2-\frac{1}{2d}M\frac{m^2(v_0-v_1)^2}{M^2}\tag{4}\] \[F=\frac {m}{2d}[v_0^2-v_1^2-\frac {m}{M}(v_0-v_1)^2]\] \[F=\frac {0.004}{2{\cdot}0.25}[600^2-100^2-\frac {0.004}{1}(600-100)^2]\, \mathrm{N}\] \[F=2792\,\mathrm{N}\,\dot=2.8\ \mathrm{kN}\]Answer:
The pendulum rises into the vertical height h = 0.2 m.
The force that slows down the bullet inside the pendulum is \[F=2792\,\mathrm{N}\,\dot=2.8\ \mathrm{kN}\] .




