Rocket
Task number: 4318
A rocket of a mass \(M_r=2\,\mathrm{t}\) loaded with a propellant of a mass \(M_p=12\,\mathrm{t}\) is powered by a rocket engine whose exhaust velocity is \(v_e=5000\,\mathrm{km\cdot h^{-1}}\). What is the maximal fuel consumption per second possible, how long can the rocket engine under such a consumption operate and what is the final speed of the rocket?
The maximal acceleration of the crew allowed is \(7 \, g\), where \(g\) stands for the gravitational acceleration.
Notation
\(M_r=2\,\mathrm{t}\) … mass of the rocket without the propellant
\(M_p=12\,\mathrm{t}\) … mass of the propellant
\(v_e = 5000\,\mathrm{km\cdot h^{-1}}\) … exhaust velocity of the rocket
\(a_{max}=7g\) … maximal acceleration
\(\left|\frac{dm}{dt}\right|_{max} =? \mathrm{kg\cdot s^{-1}}\) … maximal fuel consumption per second
\(\tau= ? \mathrm{s}\) … time of operation of the rocket engine
\(v_f= ? \mathrm{km\cdot h^{-1}}\) … final speed of the rocket
Theory
We will derive the movement of the rocket in a few steps.
We first consider the rocket to be in an isolated system, i.e., we consider only the rocket to be located in our system with no external forces acting on it and not being in any force field. The rocket is moving with velocity \(\vec v\) with respect to an inertial frame of reference. It must expel propellant (exhaust gases) to accelerate. Let’s assume that it expels a mass \(\mathrm{d}m\) of the exhaust gases during the time interval \(\mathrm{d}t\) and that the velocity of those gases with respect to the inertial frame of reference is \(\vec {v_p}\). The velocity of the rocket is thus increased by \(\mathrm{d}\vec v\).
We can obtain the velocity of the expelled exhaust gases with respect to the inertial frame of reference as a superposition of the velocity of the rocket \(\vec v\) and the velocity \(\vec {v_e}\) of the exhaust gases with respect to the rocket. We write \(\vec {v_p}=\vec v + \vec{v_e}\). The velocity \(\vec {v_e}\) is called the exhaust velocity.
The law of conservation of momentum holds in our isolated system. We can denote it as follows:
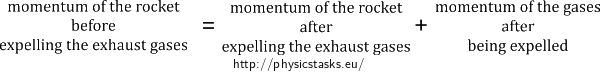
The motion of the rocket is depicted in the following figure; we can see the situation in the initial time \(t\) and then after passing the time interval \(\mathrm{d}t\) when the exhaust gases of the mass \(\mathrm{d}m\) are expelled.

We write the law of conservation of momentum for the rocket in an isolated system as follows:
\[m\vec v = \left(m-|\mathrm{d}m|\right)\left(\vec v + \mathrm{d}\vec v\right) + |\mathrm{d}m|\vec{v_p}.\]
Let us now consider the motion of the rocket in a gravitational field so that the gravitational force acts against the direction in which the rocket was launched. We will use Meshchersky’s equation in this case.
To derive the equation, we begin with change in momentum of a body being equal to the impulse of the force acting on it:
\[\vec p (t+\mathrm{d}t) - \vec p (t) = \vec F \mathrm{d}t,\] \[\left(m-|\mathrm{d}m|\right)\left(\vec v + \mathrm{d}\vec v\right) + |\mathrm{d}m|\vec{v_p} - m\vec v = \vec F \mathrm{d}t.\]Simplifying the equation and neglecting the term \(\mathrm{d}m \mathrm{d}\vec v\) we get:
\[m\mathrm{d}\vec v + |\mathrm{d}m|(\vec{v_p} - \vec v) = \vec F \mathrm{d}t.\]We divide the equation by \(\mathrm{d}t\), remove the absolute value of \(\mathrm{d}m\) and substitute the exhaust velocity \(\vec {v_e}\) for the difference of velocities \(\vec{v_p} - \vec v\). We obtain the Meshchersky’s equation:
\[m\frac{\mathrm{d}\vec v}{\mathrm{d}t}=\vec F + \vec {v_e}\frac{\mathrm{d}m}{\mathrm{d}t},\]
where \(\vec F\) is the force acting on the body in the given field. In our case, it is the gravitational force acting on the rocket. We can thus substitute the expression \(m\vec g\) for the gravitational force into the Meshchersky’s equation:
\[m\frac{\mathrm{d}\vec v}{\mathrm{d}t}=m\vec g + \vec {v_e}\frac{\mathrm{d}m}{\mathrm{d}t}.\]
We know that the gravitational force is acting in a direction opposite to the direction of the motion of the rocket. The direction of the velocity of the exhaust gases is also opposite to the direction of the motion of the rocket. Choosing the direction of the motion of the rocket to have the positive sign, we write:
\[m\frac{\mathrm{d}v}{\mathrm{d}t}=-mg - {v_e}\frac{\mathrm{d}m}{\mathrm{d}t}.\tag{1}\]
We now aim to determine the final speed of the rocket \(v_{f}\).
Multiplying the equation (1) by \(\mathrm{d}t\) we get:
\[m\mathrm{d}v = -mg\mathrm{d}t - v_e\mathrm{d}m.\]Dividing the equation by \(m\) gives us:
\[\mathrm{d}v= -v_e\frac{\mathrm{d}m}{m} - g\mathrm{d}t,\tag{2}\]
where \(\mathrm{d}v\) is a very small change in the rocket’s speed.
To determine the final speed of the rocket \(v_{f}\) we must integrate the equation over the whole time of operation of the rocket engine. The engine starts operating at time 0 and stops its activity at the time we denote as \(\tau\). The speed of the rocket changes during that time interval from the initial speed \(v_0\) to the rocket’s final and maximal speed \(v_{f}\). The mass changes during that time interval from the initial value \(m_0\) (which is the mass of the rocket and the propellant together) to the final value \(m_f\) (which is the mass of the rocket alone).
From the equation (2) we thus get:
\[\int_{v_0}^{v_{f}}1\,\mathrm{d}v=-v_e\,\int_{m_0}^{m_f}{\frac{1}{m}}\,\mathrm{d}m -g\int_0^{\tau}1\,\mathrm{d}t,\]
\[[v]_{v_0}^{v_{f}}=-v_e [\ln m]_{m_0}^{m_f}-g[t]_0^{\tau},\]
\[v_{f}-v_0=v_e\ln{\frac{m_0}{m_f}}-g\tau.\tag{3}\]
The equation we have just obtained is termed the Tsiolkovsky rocket equation and it gives the relationship for the maximal speed of the rocket which can be obtained after a given time of the operation of the rocket engine. The maximal speed is a function of the mass of the propellant and the mass of the rocket alone.
Hint I
Start with Meshchersky’s equation and express the acceleration of the rocket from it. For which mass of the rocket will the acceleration be maximal?
Hint II
We are able to express the maximal fuel consumption and we know the mass of the propellant. Use it to express the time of operation of the rocket engine.
Hint III
Use the Tsiolkovsky rocket equation derived in the theory part (see theory) to find the final speed of the rocket.
Complete solution
We start with equation (2) for a very small change in the rocket’s speed which we derived from Meshchersky’s equation in the theory (see theory) section.
\[dv=-v_e\frac{\mathrm{d}m}{m}-g\mathrm{d}t.\]
The task assignment gives us a condition for maximal acceleration. Acceleration is the change in speed with respect to a change in time and thus adjusting the above equation we get:
\[a=\frac{\mathrm{d}v}{\mathrm{d}t}=-\frac{v_e}{m}\frac{\mathrm{d}m}{\mathrm{d}t}-g.\tag{4}\]
The term \(\frac{\mathrm{d}m}{\mathrm{d}t}\) stands for fuel consumption per second which can be considered constant. Following steps lead us to determine the maximal fuel consumption per second possible:
The acceleration \(a\) is maximal when the mass of the rocket as a whole (i.e. with the propellant) is minimal. The rocket is lightest just before the end of operation of the rocket engine when it burns all the propellant and carries only its own mass, i.e. when \(m=M_r\).
We know that the maximal acceleration allowed is a multiple of the gravitational acceleration \(g\):
\[a_{max}=7g.\]
Let’s denote the acceleration generally as an n-multiple of the gravitational acceleration (n stands for a natural number). Substituting this and the minimal mass (which leads to the maximal acceleration of the rocket) to the equation (4), we get:
\[a=ng=-\frac{v_e}{M_r}\frac{\mathrm{d}m}{\mathrm{d}t}-g.\tag{5}\]
We want to determine the maximal fuel consumption per second, i.e. the value of \(\left(\frac{\mathrm{d}m}{\mathrm{d}t}\right)_{max}\). From the equation (5), we have:
\[\left(\frac{\mathrm{d}m}{\mathrm{d}t}\right)_{max}= -\left(n+1\right)g\frac{M_r}{v_e}.\]
The mass of the fuel decreases, i.e. \(\left(\frac{\mathrm{d}m}{\mathrm{d}t}\right)_{max}\) is negative. When substituting numbers, we take the absolute value:
\[\left|\left(\frac{\mathrm{d}m}{\mathrm{d}t}\right)_{max}\right|=\left(7+1\right)\cdot9.81\cdot\frac{2000}{1388.89}\,\mathrm{kg\cdot s^{-1}}=113.0\,\mathrm{kg\cdot s^{-1}}.\]
Knowing the mass of the fuel consumed per \(1\,\mathrm{s}\) of the rocket engine operation, we want to determine the total time of operation of the engine. To do so, we divide the total mass of the propellant by its consumption per second. Thus:
\[\tau = \frac{M_p}{\left|\left(\frac{\mathrm{d}m}{\mathrm{d}t}\right)_{max}\right|}=\frac{M_pv_e}{(n+1)gM_r}.\]
After substitution, we have:
\[\tau =\frac{12000{\cdot} 1388.89}{(7+1)\cdot 9.81{\cdot} 2000}\,\mathrm {s}=106.2\,\mathrm{s}.\]
It remains to determine the final speed of the rocket \(v_f\). We use the Tsiolkovsky rocket equation (3), whose derivation is described in detail in the section theory. Substituting the mass from the task assignment and the expression of the total time of operation \(\tau\), we get:
\[v_f=v_e\ln{\frac{M_r +M_p}{M_r}}-g\frac{M_pv_e}{(n+1)gM_r}=v_e\ln{\frac{M_r +M_p}{M_r}}-\frac{M_pv_e}{(n+1)M_r}.\]
We substitute all the values:
\[v_f= (5000\cdot\ln{\frac{2000 +12000}{2000}}-\frac{12000{\cdot}5000}{(7+1)\cdot 2000})\,\mathrm{km\cdot h^{-1}}\doteq 6000\,\mathrm{km\cdot h^{-1}},\]
which gave us the answer to the last question from the task assignment.
Answer
The maximal fuel consumption per second is generally given by the following equation:
\[\left|\left(\frac{\mathrm{d}m}{\mathrm{d}t}\right)_{max}\right|=\left(n+1\right)g\frac{M_r}{v_e}\]
and for our rocket, it equals \(113\,\mathrm{kg\cdot s^{-1}}\).
The time of operation of the rocket engine with such power is:
\[\tau=\frac{M_pv_e}{(n+1)gM_r}=106\,\mathrm{s}.\]
The final speed of the rocket is \(6000\,\mathrm{km\cdot h^{-1}}\) and generally, it is described as follows:
\[v_f=v_e\ln{\frac{M_r +M_p}{M_r}}-\frac{M_pv_e}{(n+1)M_r}.\]




