Collection of Solved Problems in Physics

Angle grinder disc

Task number: 1997

• Hint 1 for a): A picture of the situation

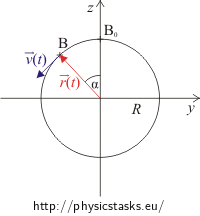
  Draw a picture, mark the initial position of point B - the position B₀ - and its position at time t. Mark the angle α, by which the point has rotated over time t, as well. Write down the coordinates of point B in time t using disk’s radius and the angle α.

• Solution of Hint 1:

  Picture 1:

  

  Coordinates of point B :

  \[y\,=\,-R\,\sin\alpha,\] \[z\,=\,R\,\cos\alpha.\]

• Hint 2 for a): Angular velocity of the disc

  The disk is rotating with constant acceleration ε. How does angular velocity ω change with time, how does angle α?

• Solution of Hint 2:

  Calculation of magnitude of angular velocity ω and of angle α

  \[\varepsilon\,=\,\mathrm{const.},\] \[\omega\,=\,\int{\varepsilon}\,\mathrm{d}t\,=\,\varepsilon{t}+C.\]

  We determine the constant C from initial conditions.

  For t = 0 is \(\omega = 0\), so:

  \[0\,=\,0+C\,.\]

  Therefore C = 0.

  \[\omega\,=\,\varepsilon t\,.\]

  For angle α, the following applies:

  \[\alpha\,=\,\int{\omega}\,\mathrm{d}t\,=\, \int{\varepsilon t}\,\mathrm{d}t\,=\, \frac{1}{2}\varepsilon{t^{2}}+K\,.\]

  We determine the constant K from initial conditions.

  For t = 0 is \(\alpha\,=\,0\), so:

  \[0\,=\,0+K\,.\]

  Therefore K = 0.

  \[\alpha\,=\,\frac{1}{2}\varepsilon{t^{2}}\,.\tag{1}\]

• Hint 3 for a): position vector of point B

  You know how the coordinates of point B change. Use them to write the position vector.

• Solution of Hint 3:

  Position vector of B:

  \[\vec{r}\left(t\right)\,=\, y\vec{j}+ z\vec{k}\,, \]

  where \(\vec{j}\), \(\vec{k}\) are unit vectors in the directions of axes y and z.

  \[\vec{r}\left(t\right)\,=\,-R\,\sin\alpha\vec{j}+ R\,\cos\alpha\vec{k}.\]

  We substitute for α from equation (1):

  \[\vec{r}(t)\,=\,-R\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}+R\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,. \tag{2}\]

• Hint 4 for a): Velocity of point B

  How do you get from x(t) and y(t) to components of velocity v_x(t) and v_y(t)? Use them to write down the velocity vector \(\vec{v}\left(t\right)\).

• Solution of Hint 4:

  For the velocity of point B on the circumference of the disc, the following applies:

  \[\vec{v}\left(t\right)\,=\,\frac{\mathrm{d}\vec{r}\left(t\right)}{\mathrm{d}t}\,=\,\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}\vec{j}+\frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}\vec{k}\,,\] \[v_y\,=\,\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(-R\,\sin\frac{\varepsilon t^2}{2}\right)\,=\, -R\varepsilon t\,\cos\frac{\varepsilon{t^{2}}}{2}\,,\] \[v_z\,=\,\frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(R\,\cos\frac{\varepsilon{t^{2}}}{2}\right)\,=\, -R\varepsilon t\,\sin\frac{\varepsilon{t^{2}}}{2}\,,\] \[\vec{v}\left(t\right)\,=\, v_y\left(t\right)\vec{j}+ v_z\left(t\right)\vec{k}\,,\] \[\vec{v}\left(t\right)\,=\,-R\varepsilon t\,\cos\frac{\varepsilon t^2}{2}\vec{j}-R\varepsilon t\,\sin\frac{\varepsilon t^2}{2}\vec{k}\,,\tag{3}\]

  where \(\vec{j}\), \(\vec{k}\) are unit vectors in the directions of axes y and z

   

  For speed it holds:

  \[v\left(t\right)\,=\,\sqrt{v_y^2+v_z^2}\,=\,R\varepsilon t\sqrt{\cos^{2}{\frac{\varepsilon{t^{2}}}{2}} + \sin^{2}\frac{\varepsilon t^2}{2}} \,=\, R\varepsilon t\,.\tag{4}\]

• Hint 5 for a): Total acceleration of point B

  Use the technique that you already used for getting velocity from coordinates – get components of the total acceleration from the components of velocity. Then use these components to write down the acceleration vector.

• Solution of Hint 5:

  Acceleration:

  \[\vec{a}\left(t\right)\,=\,\frac{\mathrm{d}\vec{v}\left(t\right)}{\mathrm{d}t} \,=\,\frac{\mathrm{d}v_y\left(t\right)}{\mathrm{d}t}\vec{j}+\frac{\mathrm{d}v_z\left(t\right)}{\mathrm{d}t}\vec{k}\,,\]

  \[a_y\,=\,\frac{\mathrm{d}v_y\left(t\right)}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(-R\varepsilon t\,\cos\frac{\varepsilon t^2}{2}\right)\,,\]

  \[a_y\, =\, -R\varepsilon\,\cos\frac{\varepsilon t^2}{2}+R\varepsilon^2t^2\,\sin\frac{\varepsilon t^2}{2}\,,\]

  \[a_z\,=\,\frac{\mathrm{d}v_z\left(t\right)}{\mathrm{d}t} \,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(-R\varepsilon t\,\sin\frac{\varepsilon t^2}{2}\right)\,,\]

  \[a_z\,=\, -R\varepsilon\,\sin\frac{\varepsilon t^2}{2}-R\varepsilon^2t^2\,\cos\frac{\varepsilon t^2}{2}\,,\]

  \[\vec{a}\left(t\right)\,=\, a_y\left(t\right)\vec{j}+ a_z\left(t\right)\vec{k}\,,\]

  \[\vec{a}\left(t\right)\,=\,\left(R\varepsilon^2t^2\,\sin\frac{\varepsilon t^2}{2}-R\varepsilon\,\cos\frac{\varepsilon t^2}{2}\right)\vec{j}-\left(R\varepsilon\,\sin\frac{\varepsilon t^2}{2}+R\varepsilon^2t^2\,\cos\frac{\varepsilon t^2}{2}\right)\vec{k}\,,\]

  where \(\vec{j}\), \(\vec{k}\) are unit vectors in the directions of axes y and z.

• Hint 6 for b): Tangential acceleration

  First calculate the magnitude of tangential acceleration.

  In what direction does it point?

  How do you write a unit vector in the direction of velocity?

• Solution of Hint 6:

  Magnitude of tangential acceleration:

  \[a_t\left(t\right)\,=\,\frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}\,=\,\frac{\mathrm{d}}{\mathrm{d}t}\left(R\varepsilon t\right)\,=\,R\varepsilon\,.\]

  Tangential acceleration has the same direction as velocity:

  \[\vec{a}_t\,=\,a_t\vec{v}_{ok}\,,\]

  where \(\vec{v}_{ok} \)  is a unit vector in the direction of velocity.

  We get a unit vector when we divide a vector by its magnitude, so:

  \[\vec{v}_{ok}\,=\,\frac{\vec{v}}{v}\,.\]

  Dividing (3) by (4) we get:

  \[\vec{v}_{ok} \,=\,\frac{\vec{v}}{v} \,=\, -\cos\frac{\varepsilon t^2}{2}\vec{j}-\sin\frac{\varepsilon t^2}{2}\vec{k}\,,\]

  where \(\vec{j}\), \(\vec{k}\) jsoare unit vectors in the direction of axes y and z.

  So, the tangential acceleration equals:

  \[\vec{a}_t\left(t\right)\,=\, a_t\vec{v}_{ok} \,=\, -R\varepsilon\,\cos\frac{\varepsilon t^2}{2}\vec{j}-R\varepsilon\,\sin\frac{\varepsilon t^2}{2}\vec{k}\,.\]

• Hint 7 for c): Normal acceleration

  First count calculate the magnitude of normal acceleration.

  In what direction does it point?

  How do you write a unit vector in the direction of the position vector?

  Knowing the magnitude of tangential acceleration and the unit vector in its direction, you can easily write the vector of tangential acceleration.

• Solution for Hint 7:

  Magnitude of normal acceleration:

  \[a_n\,=\,\frac{v^{2}}{R}\,=\,\frac{R^{2}\varepsilon^{2}t^{2}}{R}\,=\,R\varepsilon^{2}t^{2}\,.\]

  Normal acceleration has the same direction, yet opposite orientation as position vector.

  \[\vec{a}_n\left(t\right)\,=\, a_n \left(- \vec{r}_o\right)\,,\]

  where \(\vec{r}_o\) is a unit vector in the direction of the position vector.

  We get a unit vector if we divide a vector by its magnitude, so:

  \[\vec{r}_o\,=\,\frac{\vec{r}}{R}\,.\]

  Dividing (2) by radius R we get:

  \[\vec{r}_o \,=\,\frac{\vec{r}}{R} \,=\, -\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}+\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,,\]

  where \(\vec{j}\), \(\vec{k}\) are unit vectors in the directions of axes y and z.

  Normal acceleration then equals:

  \[\vec{a}_n\left(t\right)\,=\, a_n \left(- \vec{r}_o\right) \,=\, R\varepsilon^{2}t^{2}\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}- R\varepsilon^{2}t^{2}\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,.\]

  Note: Tangential and normal acceleration are perpendicular. Another way to get the unit vector in the direction of normal acceleration is to take a vector perpendicular to the unit vector in the direction of tangential acceleration.

• Solution 8 for d): Angle between total and normal acceleration

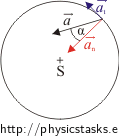
  Draw a picture where you mark normal, total and tangential acceleration and the angle you want to find. What trigonometric function binds these together?

  You will also need the magnitude of total acceleration. Use your knowledge of a_t and a_n or a_y and a_z.

• Solution for Hint 8:

  Picture 2:

  

   

  For angle α, the following applies:

  \[\cos\alpha\,=\,\frac{a_n}{a}\,.\tag{5}\]

  Calculation of magnitude of total acceleration a:

  \[a\,=\,\sqrt{a_t^{2}+a_n^{2}} \,=\,\sqrt{(R\varepsilon)^{2}+ (R\varepsilon^{2}t^{2})^{2}}\,=\, R\varepsilon\sqrt{1+\varepsilon^{2}t^{4}}\,.\]

  Plot in (5):

  \[\cos\alpha\,=\,\frac{a_n}{a}\,=\,\frac{R\varepsilon^{2}t^{2}}{R\varepsilon\sqrt{1+\varepsilon^{2}t^{4}}}\,=\,\left(1+\frac{1}{\varepsilon^{2}t^{4}}\right)^{-\frac{1}{2}}\,.\]

• CELKOVÉ ŘEŠENÍ

  a) Position vector of point B

  We draw a picture of the situation.

  Picture 1:

  

  Coordinates of point B :

  \[y\,=\,-R\,\sin\alpha,\] \[z\,=\,R\,\cos\alpha.\]

   

  Calculation of magnitude of angular velocity ω and of angle α:

  \[\varepsilon\,=\,\mathrm{const.}\,,\] \[\omega\,=\,\int{\varepsilon}\,\mathrm{d}t\,=\,\varepsilon{t}+C\,.\]

  We determine the constant C from initial conditions.

  For t = 0 is \(\omega \,=\,0\), so:

  \[0\,=\,0+C\,.\]

  Therefore C = 0.

  \[\omega \,=\, \varepsilon t\,.\]

   

  For angle α, following applies:

  \[\alpha\,=\,\int{\omega}\,\mathrm{d}t\,=\, \int{\left(\varepsilon t\right)\mathrm{d}t} \,=\, \frac{1}{2}\varepsilon{t^{2}}+K\,.\]

  We determine the constant K from initial conditions.

  For t = 0 is α = 0, so:

  \[0\,=\,0+K\,.\]

  Therefore K = 0.

  \[ \alpha\,=\,\frac{1}{2}\varepsilon{t^{2}}\,.\tag{1}\]

   

  Position vector of point B:

  \[\vec{r}\left(t\right)\,=\, y\vec{j}+ z\vec{k}\,,\]

  where \(\vec{j}\), \(\vec{k}\) are unit vectors in the directions of axes y and z.

  \[\vec{r}\left(t\right)\,=\,-R\,\sin\alpha\vec{j}+ R\,\cos\alpha\vec{k}\,.\]

  We substitute for α from equation (1):

  \[\vec{r}\left(t\right)\,=\,-R\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}+R\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,.\tag{2}\]

   

  a) Velocity of point B

  For the velocity of point B on the circumference of the disc, the following applies:

  \[\vec{v}\left(t\right)\,=\,\frac{\mathrm{d}\vec{r}\left(t\right)}{\mathrm{d}t}\,=\,\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}\vec{j}+\frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}\vec{k}\,,\] \[v_y\,=\,\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(-R\,\sin\frac{\varepsilon{t^{2}}}{2}\right)\,=\, -R\varepsilon{t}\,\cos\frac{\varepsilon{t^{2}}}{2}\,,\] \[v_z\,=\,\frac{\mathrm{d}z\left(t\right)}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}(R\,\cos\frac{\varepsilon{t^{2}}}{2})\,=\, -R\varepsilon{t}\,\sin\frac{\varepsilon{t^{2}}}{2}\,,\] \[\vec{v}\left(t\right)\,=\, v_y\left(t\right)\vec{j}+ v_z\left(t\right)\vec{k}\,,\] \[\vec{v}\left(t\right)\,=\,-R\varepsilon{t}\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{j}-R\varepsilon{t}\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{k}\,,\tag{3}\]

  where \(\vec{j}\), \(\vec{k}\) are unit vectors in the directions of awes y and z.

   

  For speed it holds:

  \[ v\left(t\right)\,=\,\sqrt{v_y^{2}+v_z^{2}}\,=\,R\varepsilon t\sqrt{\cos^{2}{\frac{\varepsilon t^2}{2}} + \sin^{2}{\frac{\varepsilon t^2}{2}}}\,=\, R\varepsilon t\,.\tag{4}\]

   

  a) Total acceleration of point B

  Acceleration:

  \[\vec{a}\left(t\right)\,=\,\frac{\mathrm{d}\vec{v}\left(t\right)}{\mathrm{d}t} \,=\,\frac{\mathrm{d}v_y\left(t\right)}{\mathrm{d}t}\vec{j}+\frac{\mathrm{d}v_z\left(t\right)}{\mathrm{d}t}\vec{k}\,,\] \[a_y\,=\,\frac{\mathrm{d}v_y\left(t\right)}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(-R\varepsilon t\,\cos\frac{\varepsilon{t^{2}}}{2}\right)\,,\] \[a_y\,=\, -R\varepsilon\,\cos\frac{\varepsilon{t^{2}}}{2}+R\varepsilon^{2}t^{2}\,\sin\frac{\varepsilon{t^{2}}}{2}\,,\] \[a_z\,=\,\frac{\mathrm{d}v_z\left(t\right)}{\mathrm{d}t} \,=\, \frac{\mathrm{d}}{\mathrm{d}t}(-R\varepsilon{t}\,\sin\frac{\varepsilon{t^{2}}}{2})\,,\] \[a_z\,=\, -R\varepsilon\,\sin\frac{\varepsilon{t^{2}}}{2}-R\varepsilon^{2}t^{2}\,\cos\frac{\varepsilon{t^{2}}}{2}\,,\] \[\vec{a}\left(t\right)\,=\, a_y\left(t\right)\vec{\,j\,}+ a_z\left(t\right)\vec{\,k\,}\,,\]

  \[\vec{a}\left(t\right)=\left(R\varepsilon^{2}t^{2}\,\sin\frac{\varepsilon{t^{2}}}{2}-R\varepsilon\cos\frac{\varepsilon{t^{2}}}{2}\right)\vec{j}-\left(R\varepsilon\sin\frac{\varepsilon{t^{2}}}{2}+R\varepsilon^{2}t^{2}\,\cos\frac{\varepsilon{t^{2}}}{2}\right)\vec{k}\,,\]

  where \(\vec{j}\), \(\vec{k}\) are unit vectors in the directions of axes y and z.

   

  b) Tangential acceleration of point B

  Magnitude of tangential acceleration:

  \[a_t\left(t\right)\,=\,\frac{\mathrm{d}v\left(t\right)}{\mathrm{d}t}\,=\,\frac{\mathrm{d}}{\mathrm{d}t}\left(R\varepsilon{t}\right)\,=\,R\varepsilon\,.\]

  Tangential acceleration has the same direction as velocity:

  \[\vec{a}_t\,=\,a_t\vec{v}_{ok}\,. \]

  where \(\vec{v}_{ok} \)  is a unit vector in the direction of velocity.

  We get a unit vector when we divide a vector by its magnitude, so:

  \[\vec{v}_{ok}\,=\,\frac{\vec{v}}{v}\,.\]

  Dividing (3) by (4) we get:

  \[\vec{v}_{ok} \,=\,\frac{\vec{v}}{v} \,=\, -\cos\frac{\varepsilon{t^{2}}}{2}\vec{j}-\sin\frac{\varepsilon{t^{2}}}{2}\vec{k}\,,\]

  where \(\vec{j}\), \(\vec{k}\) are unit vectors in the directions of axes y and z.

  So, the tangential acceleration equals:

  \[\vec{a}_t\left(t\right)\,=\, a_t\vec{v}_{ok} \,=\, -R\varepsilon\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{\,j\,}-R\varepsilon\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{\,k\,}\,.\]

   

  c) Normal acceleration of point B

  Magnitude of normal acceleration:

  \[a_n\,=\,\frac{v^{2}}{R}\,=\,\frac{R^{2}\varepsilon^{2}t^{2}}{R}\,=\,R\varepsilon^{2}t^{2}\,.\]

  Normal acceleration has the same direction, yet opposite orientation as position vector.

  \[\vec{a}_n\left(t\right)\,=\, a_n \left(- \vec{r}_o\right)\,,\]

  where \(\vec{r}_o\)  is a unit vector in the direction of the position vector.

  We get a unit vector if we divide a vector by its magnitude, so:

  \[\vec{r}_o\,=\,\frac{\vec{r}}{r}\,.\]

  Dividing (2) by radius R we get:

  \[\vec{r}_o \,=\,\frac{\vec{r}}{r} \,=\, -\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}+\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,,\]

  where \(\vec{j}\), \(\vec{k}\) are unit vectors in the directions of axes y and z..

  Normal acceleration then equals:

  \[\vec{a}_n\left(t\right)\,=\, a_n \left(- \vec{r}_o\right)\,=\, R\varepsilon^{2}t^{2}\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}- R\varepsilon^{2}t^{2}\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,.\]

   

  Note: Tangential and normal acceleration are perpendicular. Another way to get the unit vector in the direction of normal acceleration is to take a vector perpendicular to the unit vector in the direction of tangential acceleration.

   

  d) Angle α between total and normal acceleration

  Picture 2:

   

  

   

  For angle α, the applies:

  \[\cos\alpha\,=\,\frac{a_n}{a}\,.\tag{5}\]

  Calculation of magnitude of total acceleration a:

   

  \[a\,=\,\sqrt{a_t^{2}+a_n^{2}} \,=\,\sqrt{\left(R\varepsilon\right)^{2}+ \left(R\varepsilon^{2}t^{2}\right)^{2}}\,=\, R\varepsilon\sqrt{1+\varepsilon^{2}t^{4}}\,.\]

  Plot in (5):

  \[\cos\alpha\,=\,\frac{a_n}{a}\,=\,\frac{R\varepsilon^{2}t^{2}}{R\varepsilon\sqrt{1+\varepsilon^{2}t^{4}}}\,=\,\left(1+\frac{1}{\varepsilon^{2}t^{4}}\right)^{-\frac{1}{2}}\,.\]

• Odpověď

  a) Position vector of point B:

  \[\vec{r}(t)\,=\,-R\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}+R\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,. \]

  Velocity of point B:

  \[\vec{v}\left(t\right)\,=\,-R\varepsilon{t}\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{j}-R\varepsilon{t}\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{k}\,.\]

  Total acceleration of point B:

  \[\vec{a}\left(t\right)=\left(R\varepsilon^{2}t^{2}\sin\frac{\varepsilon{t^{2}}}{2}-R\varepsilon\cos\frac{\varepsilon{t^{2}}}{2}\right)\vec{j}-\left(R\varepsilon\,\sin\frac{\varepsilon{t^{2}}}{2}+R\varepsilon^{2}t^{2}\,\cos\frac{\varepsilon{t^{2}}}{2}\right)\vec{k}\,,\]

  where \(\vec{j}\), \(\vec{k}\) are unit vectors in the directions of axes y and z.

  b) Tangential acceleration:

  \[\vec{a}_t\left(t\right)\,=\,-R\varepsilon\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{j}-R\varepsilon\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{\,k\,}\,,\]

  where \(\vec{j}\), \(\vec{k}\) are unit vectors in the directions of axes y and z.

   

  c) Normal acceleration:

  \[\vec{a}_n\left(t\right)\,=\,\varepsilon^{2}Rt^{2}\,\sin\frac{\varepsilon{t^{2}}}{2}\vec{j}- \varepsilon^{2}Rt^{2}\,\cos\frac{\varepsilon{t^{2}}}{2}\vec{k}\,,\]

  where \(\vec{j}\), \(\vec{k}\) are unit vectors in the directions of axes y and z.

   

  d) Angle α between total and normal acceleration:

  \[\cos\alpha\,=\,\frac{a_n}{a}\,=\,\frac{R\varepsilon^{2}t^{2}}{R\varepsilon\sqrt{1+\varepsilon^{2}t^{4}}}\,=\,\left(1+\frac{1}{\varepsilon^{2}t^{4}}\right)^{-\frac{1}{2}}\,.\]