Thread on a pulley
Task number: 931
We have a thread wound four times around pulley wheel with a diameter of 30 cm and mass of 5 kg. We want to unwind the thread by pulling it in 1 second. What minimal constant force do we need to pull the thread?
Notation:
m = 5 kg mass of the pulley r = 15 cm diameter of the pulley’s wheel n = 4 number of windings around the wheel t = 1 s time to unwind F = ? (N) minimal constant force needed for pulling the thread Moment of inertia:
We consider the pulley to be a cylinder with mass m and diameter r. We can find a formula for moment of inertia for cylinder regarding the geometric axis:
\[J=\frac{1}{2} mr^2 \,.\tag{0}\](Finding the form of this formula will be a part of another task.)
Analysis
The task can be solved either by the usage of the second impulse theorem \(\vec{M}=\frac{\mathrm{d}\vec{L}}{\mathrm{d}t}\).
Otherwise, we can use the law of conservation of energy. The work, we perform by pulling the thread, transforms into the kinetic energy of the pulley.
Hint A1 – Second impulse theorem
Draw a picture of the situation, mark the forces affecting the pulley. Write down the second impulse theorem for the pulley.
Hint A2 – Second impulse theorem
What can we say about the angular acceleration of the pulley? Figure out how the angle of the pulley wheel rotation changes in relation to time. Be aware of the fact that you know this angle, as the number of windings around the wheel is given.
Hint B1 – Law of energy conservation
Figure out, what the work, which we perform by pulling the thread, equals to. Realize what the work is used for.
Hint B2 – Law of energy conservation
What type of movement does the tip of the thread perform? Express its velocity in the moment of unwinding of all threads.
Complete solution – Second impulse theorem
We draw a picture of the situation, mark the forces affecting the pulley. We write down the second impulse theorem for the pulley.
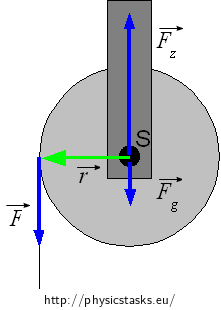
The pulley is affected by the weight force Fg, hanging by the Fz and by the force we pull the thread F with.
Second impulse theorem says:
\[\vec{M}=\frac{\mathrm{d}\vec{L}}{\mathrm{d}t}\,.\]In case of rotating of the rigid body around fixed axis:
\[L = J \omega\,,\] \[\vec{M}=\frac{\mathrm{d}\vec{L}}{\mathrm{d}t} = J\vec{\epsilon}\,,\]where \(\vec{M}\) is a resultant moment of the forces affecting the thread regarding a chosen point and \(\vec{L}\) is a resultant angular momentum regarding the point. \(J\) means moment of inertia regarding the fixed axis going through the chosen point and \(\vec{\epsilon}\) means angular acceleration of the pulley.
For the resultant moment of the force system regarding the centre of the pulley hold true the following:
\[ \vec{M}=\vec{r}\times\vec{F} = J\vec{\epsilon}\,.\]We rewrite this formula into scalar form and substitute for the moment of inertia:
\[M = rF = \frac{1}{2} mr^2\epsilon\,.\]We express the angular acceleration of the pulley:
\[\epsilon =\frac{F}{\frac{1}{2} mr}\,.\tag{1}\]Angular acceleration of the pulley is constant. The angle, by which a point on the edge of pulley wheel rotates in time t, can be expressed as follows:
\[\alpha = \frac{1}{2}\epsilon\, t^2\tag{2}\]We know that we have to unwind n threads, so the pulley wheel shall be rotated by an angle:
\[\alpha = n 2\pi\]Using the form (2) we can say:
\[\alpha = n 2\pi = \frac{1}{2}\epsilon t^2\]After the substitution of the angular acceleration from form (1), we get:
\[n 2\pi = \frac{1}{2}(\frac{F}{\frac{1}{2} mr})t^2 \]And rewrite into:
\[n 2\pi mr = Ft^2\]From this form we get:
\[F = \frac{2n\pi rm}{t^2}\]With numbers:
\[F = \frac{2{\cdot}4\cdot\pi\cdot 0.15{\cdot} 5}{1^2}\,\mathrm{N} \dot{=}18.9\,\mathrm{N}\,.\]Complete solution – Low of energy conservation
Work of the constant force affecting in the direction of movement is equal to:
\[W=Fs,\]where s is the distance which the tip of the thread covered during unwinding.
The work in this case is used for rotating the pulley wheel, in other words for changing the kinetic energy of the wheel.
\[ E=\frac{1}{2}J\omega^2=\frac{1}{2}(\frac{1}{2}mr^2)\omega^2= \frac{1}{4}mr^2(\frac{v}{r})^2=\frac{1}{4}mv^2.\]Where v is peripheral velocity in the moment, when unwinding is finished, that means the velocity, which we pull the thread with at the moment when all threads are unwound.
Hence:
\[Fs = \frac{1}{4}mv^2\,.\tag{3}\]Work of the constant force affecting in the direction of movement is equal to:
\[W=Fs,\]where s is the distance which the tip of the thread covered during unwinding.
The work in this case is used for rotating the pulley wheel, in other words for changing the kinetic energy of the wheel.
\[ E=\frac{1}{2}J\omega^2=\frac{1}{2}(\frac{1}{2}mr^2)\omega^2= \frac{1}{4}mr^2(\frac{v}{r})^2=\frac{1}{4}mv^2.\]Where v is peripheral velocity in the moment, when unwinding is finished, that means the velocity, which we pull the thread with at the moment when all threads are unwound.
Hence:
\[Fs = \frac{1}{4}mv^2\,.\tag{3}\]The tip of the thread performs a constant accelerated linear motion. The distance s, which it covers, can be expressed from the length of the thread wound around the pulley wheel: it is n times perimeter of the wheel, where n is the amount of windings:
\[ s=2n\pi r\,.\]To express the velocity we use following formulas:
\[ v=at\]and
\[ s=\frac{1}{2}at^2\,.\]This can be rewritten into:
\[ a=\frac{2s}{t^2}.\]For expressing the velocity we get:
\[v=at=\frac{2s}{t^2}t=\frac{2s}{t}\,.\]We substitute into the form (3):
\[Fs=\frac{1}{4}m(\frac{2s}{t})^2\,,\] \[F=m\frac{s}{t^2}\,,\] \[F=\frac{2n\pi rm}{t^2}\,.\]After inserting numbers:
\[F = \frac{2{\cdot}4\cdot\pi\cdot 0.15{\cdot} 5}{1^2}\,\mathrm{N} \dot{=}18.9\,\mathrm{N}.\]Answer
We have to pull the thread with force F:
\[ F=\frac{2nm\pi r}{t^2}\,,\] \[ F\dot{=}18.85\,\mathrm{N}.\]


