Center of gravity of unusual circle
Task number: 1519
Determine position of the center of gravity of the planar object on the picture below.
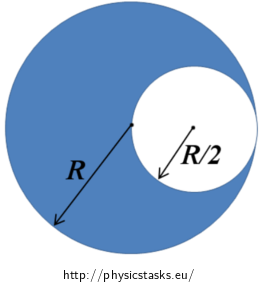
Hint 1
Think about what does mean task “determine position of the center of gravity”. What should be outcome of the task, what exactly determine?
Hint 2
Suitably place object in coordinate system. Is possible choose its position so next calculations are simpler, or some isn’t need at all?
Description of method
Position vector rT describing position of the center of gravity we usually calculate using integral:
\[\vec{r}_T\,=\,\frac{\int{\vec{r}}dm}{{\int}dm}\]Shape of examined object is atypical so gain x-coordinate of the center of gravity using integration is – gently said – enormously difficult. Therefor we try to solve this problem other way below (we restrict to planar problem). Two different perspectives on the same complex are going to help us.
Situation 1: Imagine for a while that we fill back in small cut circle. Center of gravity T1 of completed large circle with mass m is in its center, so its coordinate is xT1 = R.
Situation 2: Now completed circle divide again on:
- “bitten” object with mass m1 of which center of gravity has unknown coordinate xT
- small circle with mass m2 of which center of gravity T2 has coordinate xT2 = 3R/2
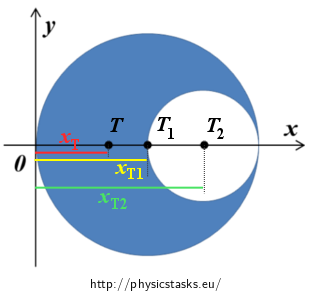
Because we describe the same examined object once as a unit and once as system of two parts, it’s obvious that center of gravity of the system “bitten” object + small circle has to be in the center of gravity of the completed circle. This idea will be starting point during next calculations.
Hint 3
Transform idea written bold in previous section “Description of method” into mathematical form. Substitute known coordinates xT1 and xT2 and express unknown xT.
Hint 4
Using areal density we calculate masses m1 and m2. Expect object is homogenous so its areal density ρ is the same everywhere.
Hint 5
Substitute masses from equations (5) and (6) into equation (4) and express unknown coordinate xT.
COMPLETE SOLUTION
Determine position of the center of gravity means determine coordinates of the center of gravity in some suitably chosen coordinate system. Because assigned object is planar (the third dimension, “height”, we omit), two coordinates of the center of gravity T [xT, yT] are outcome of the task. Picture below shows advantageous position of the object in coordinate system – left edge of the object goes through the origin of coordinates.
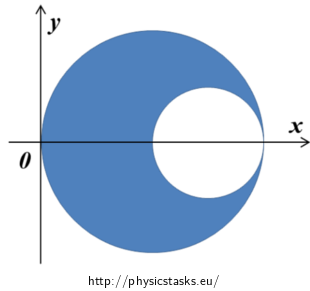
Because object placed like this is axial symmetric by xaxis its center of gravity has to lie on this axis – any point on x axis has y-coordinate zero so we can immediately write:
\[y_T\,=\,0\]It’s enough calculate only x-coordinate of the center of gravity xT onward. We usually calculate this using integral:
\[\vec{r}_T\,=\,\frac{\int{\vec{r}}dm}{{\int}dm}\]where rT is position vector describing position of the center of gravity. Shape of examined object is atypical so gain x-coordinate of the center of gravity using integration is – gently said – enormously difficult. Therefor we try to solve this problem other way below (we restrict to planar problem). Two different perspectives on the same complex are going to help us:
Situation 1: Imagine for a while that we fill back in small cut circle. Center of gravity T1 of completed large circle with mass m is in its center, so its coordinate is xT1 = R.
Situation 2: Now completed circle divide again on:
- “bitten” object with mass m1 of which center of gravity has unknown coordinate xT
- small circle with mass m2 of which center of gravity T2 has coordinate xT2 = 3R/2

Because we describe the same examined object once as a unit and once as system of two parts, it’s obvious that center of gravity of the system “bitten” object + small circle has to be in the center of gravity of the completed circle. This idea could be expressed in this mathematical form:
\[x_{T1}\,=\,\frac{m_1x_T\,+\,m_2x_{T2}}{m_1\,+\,m_2}\tag{1}\]where right side of equation is based on formula for calculation position center of gravity of the system mass points or bodies – in detail in task Těžiště různě uspořádaných soustav koulí.
Because we know coordinates xT1 and xT2 (see “Description of method”), we can substitute them into expression (1) and express xT:
\[R\,=\,\frac{m_1x_T\,+\,m_2{\cdot}\frac{3R}{2}}{m_1\,+\,m_2}\tag{2}\] \[R(m_1\,+\,m_2)\,-\,m_2\frac{3R}{2}\,=\,m_1x_T\tag{3}\] \[x_T\,=\,R(1\,-\,\frac{m_2}{2m_1})\tag{4}\]We determine mass of the small circle m2 as product of small circle’s area and areal density:
\[m_2\,=\,{\pi}\frac{R^2}{4}\varrho\tag{5}\]We can determine mass of “bitten” object m1 as difference between mass of completed circle m and mass of the small circle m2:
\[m_1\,=\,m\,-\,m_2\,=\,{\pi}R^2\varrho\,-\,{\pi}\frac{R^2}{4}\varrho\,=\,\frac{3}{4}{\pi}R^2\varrho\tag{6}\]In the end substitute from equations (5) and (6) into equation (4):
\[x_T\,=\,R(1\,-\,\frac{m_2}{2m_1})\,=\,R(1\,-\,\frac{{\pi}\frac{R^2}{4}\varrho}{2{\cdot}\frac{3}{4}{\pi}R^2\varrho})\,=\,\frac{5}{6}R\tag{7}\]Coordinate of the center of gravity “bitten” object xT is equal 5R/6.
ALTERNATIVE SOLUTION
Another method of solving is based on knowledge of work with moments. Using fact that if have (in the plain) forces acting on system of mass points or planar objects, we can determine moments to any point of plain. These forces have the same tendency to rotate the system as their resultant force acting in the center of gravity of the system. Determine individual moments at the start:
Determination of moment of gravity force – consider object as unit:
Origin of gravity force FG is in the center of gravity T examined object – lever-arm of gravity force is equal to unknown quantity xT (see picture):
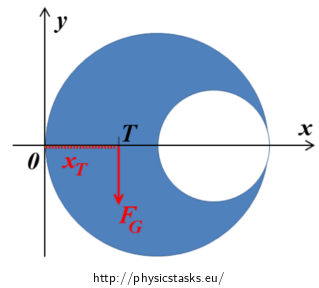
For moment of gravity force’s magnitude FG to origin of coordinates stand:
\[M_1\,=\,F_Gx_T\,=\,mgx_T\,=\,{\varrho}Sgx_T\tag{8}\]where ρ is areal density of object, S is its area and g is gravity acceleration.
We can determine area of the object according to its geometrical quality as:
\[S\,=\,{\pi}R^2\,-\,{\pi}(\frac{R}{2})^2\,=\,\frac{3}{4}{\pi}R^2\tag{9}\]By substitute from equation (9) into (8) we gain:
\[M_1\,=\,\frac{3}{4}{\pi}R^2{\varrho}g{\cdot}x_T\tag{10}\]Determine moments – object divide in two parts:
Now we consider large circle without any cuts. Gravity force FG1 acting this circle and its origin is in the center of circle and for moment of gravity force FG1 to origin of coordinates stand:
\[M_2\,=\,F_{G1}R\] Because by completion large circle with cut part we increase its mass, we’re considering effective mass of small circle negative – so we gain final mass of the object. (As if small circle lightens large completed circle.) Effective gravity force on small circle FG2 is heading upright and its origin is in the center of small circle. For moment of gravity force FG2 to origin of coordinates stand: \[M_3\,=\,F_{G2}{\cdot}\frac{3R}{2}\]Lever-arms are easy to see in the picture:
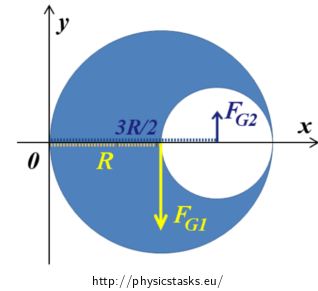
We gain resultant moment of forces FG1 and FG2 as difference partial moments (difference because forces have opposite tendency to rotate the system). For resultant moment’s magnitude M stand:
\[M\,=\,M_2\,-\,M_3\,=\,R(F_{G1}\,-\,\frac{3}{2}F_{G2})\tag{11}\]Now adjust equation (11) using areal density ρ similarly as equation (1):
\[M\,=\,Rg(m_1\,-\,\frac{3}{2}m_2)\,=\,Rg{\varrho}(S_1\,-\,\frac{3}{2}S_2)\tag{12}\]where S1 is area of large circle and S2 area of small circle. Considering geometry of the object we can write:
\[M\,=\,Rg{\varrho}({\pi}R^2\,-\,\frac{3}{2}{\pi}({\frac{R}{2}})^2)\,=\,\frac{5}{8}R^3g{\varrho}{\pi}\tag{13}\]Comparison above calculate moments:
According to base idea of our method stand:
\[M_1\,=\,M\tag{14}\]Substitute into equation (14) from equations (10) and (13) and express xT:
\[\frac{3}{4}{\pi}R^2{\varrho}g{\cdot}x_T\,=\,\frac{5}{8}R^3g{\varrho}{\pi}\] \[\frac{3}{4}x_T\,=\,\frac{5}{8}R\] \[x_T\,=\,\frac{20}{24}R\,=\,\frac{5}{6}R\]Coordinate of the center of gravity xT is equal 5R/6.
Answer
Coordinates of the center of gravity of assigned object in by us chosen coordinate system are:
\[x_T\,=\,\frac{5}{6}R\] \[y_T\,=\,0\]



