Motion on two inclined planes
Task number: 1149
In a uniform gravitational field there are two inclined planes placed back to back, perpendicular to each other. One of the planes is inclined at an angle α to the horizontal plane. At the same moment two balls of masses m1, m2 and radius R are released from joint edge down to different sides. Determine the motion of the centre of mass of system of the balls. Solve
Hint 1 - to the part A
In the first part of the task we neglect the moment of inertia of balls – in such a case, is it possible to replace the balls with simpler physical concept?
Hint 2 – to the part A
Draw a free body diagram and choose an appropriate reference frame. What does it mean „determine the motion of the centre of mass“? What should be the output of the task?
Hint 3 – to the part A
Assume that the balls roll down without friction. What accelerations do the balls experience? Draw a picture and mark all forces that affect the balls and find the accelerations, using the Newton’s second law. What type of motion is exhibited by single balls (in term of trajectory and velocity)?
Hint 4 – to the part A
Write down expressions for x and y coordinates of the ball of mass m1 as a function of time. Proceed the same way for the ball of mass m2.
Hint 5 – to the part A
At this point, we already know the way of changing the coordinates of our two balls (point masses) with time. Use then the formula that determines the coordinates of the centre of mass and solve the first part of the task.
Hint 6 – to the part B
In the second part of the task we include the moment of inertia of balls. Firstly, go through the solution of the part A and decide how far it is replicable – where the non-zero moment of inertia is relevant for the first time?
Hint 7 – to the part B
Use the law of conservation of energy to determine an acceleration of the centre of mass of balls in each coordinate direction. (Attention, it is quite long computation, integrating pieces of knowledge from different parts of mechanics!)
Commentary 1
A magnitude of acceleration of the centre of mass of both balls can be determined also with different technique, and it is with the help of the laws of conservation of momentum and angular momentum.
Hint 8 – to the part B
In previous step we obtained the magnitude of acceleration of the centre of the first ball ax and the second ball ay. Use them as components a1 and a2 in the part A and determine the change of coordinates xT´(t), yT´(t) of the centre of mass of the system with time using the same computation method.
Solution - the part A
If we neglect the moment of inertia of balls, it is possible to replace balls with point masses. The figure bellow shows the appropriate reference frame used in this problem.
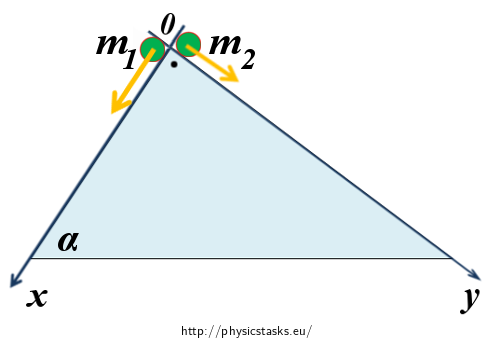
We consider that the motion is situated in the plane xy, thus we can omit the change of z-coordinate. The output of the task should be a formula which describes the change in coordinates of the centre of mass xT a yT, with time, xT(t) = ?, yT(t) = ? respectively.
The force of gravity and the normal force of the surface act on both balls. Their resultant causes the ball of mass m1 to accelerate in xdirection and the ball of mass m2 to accelerate in y direction. The figure bellow shows not only the acting force of gravity FG and normal force FN but also the components of the force of gravity aligned with the coordinate axes (in black).
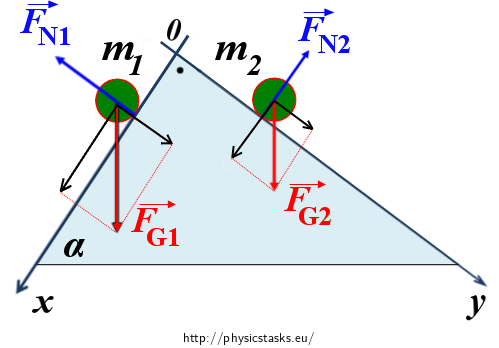
According to the Newton’s second law, for the ball of mass m1: we can derive the following equation:
\[ \vec{F}_{G1}\,+\,\vec{F}_{N1}\,=\,m_1\vec{a}_1\tag{1}\]Following the picture, we rewrite the equation (1) into scalar form:
The direction of x-axis:
\[F_{G1}\sin{\alpha}\,=\,m_1a_1\tag{2}\]The direction of y-axis:
\[F_{G1}\cos{\alpha}\,-\,F_{N1}\,=\,0\tag{3}\]By substitution of the force of gravity into equation (2), we obtain:
\[m_1g\sin{\alpha}\,=\,m_1a_1\,\Rightarrow\,a_1\,=\,g\sin{\alpha}\tag{4}\]The ball of mass m1 undergoes uniformly accelerated motion in the direction of the x axis and with the acceleration a1. In the case of the second ball we proceed analogically.
According to the Newton’s second law, for the ball of mass m2: we can derive the following equation:
\[ \vec{F}_{G2}\,+\,\vec{F}_{N2}\,=\,m_2\vec{a}_2\tag{5}\]Following the picture, we rewrite the equation (5) into scalar form:
The direction of x-axis:
\[F_{G2}\sin{\alpha}\,-\,F_{N2}\,=\,0\tag{6}\]The direction of y-axis:
\[F_{G2}\cos{\alpha}\,=\,m_2a_2\tag{7}\]After substitution of the force of gravity into equation (7), we obtain:
\[m_2g\cos{\alpha}\,=\,m_2a_2\,\Rightarrow\,a_2\,=\,g\cos{\alpha}\tag{8}\]The ball of mass m2 also undergoes uniformly accelerated motion this time in the direction of the y axis and with the acceleration a2
The ball of mass m1 undergoes uniformly accelerated motion in the direction of the x axis and with the acceleration a1:
\[x_1(t)\,=\,\frac{1}{2}a_1t^2\,=\,\frac{1}{2}g(\sin{\alpha})t^2\tag{9}\]The coordinate of the ball in the direction of y axis is identically equal to zero:
\[y_1(t)\,=\,0\tag{10}\]The ball of mass m2 undergoes uniformly accelerated motion in the direction of the y axis and with the acceleration a2:
\[y_2(t)\,=\,\frac{1}{2}a_2t^2\,=\,\frac{1}{2}g(\cos{\alpha})t^2\tag{11}\]The coordinate of the ball in the direction of x axis is identically equal to zero:
\[x_2(t)\,=\,0\tag{12}\]The centre of mass of npoint masses are given by:
\[\vec{r}_T\,=\,\frac{\sum_{i=1}^n{m_i\vec{r}_i}}{\sum_{i=1}^n{m_i}}\]where mi are masses of individual point masses and ri are their respective position vectors.
Because the coordinates of the centre of mass can be calculated for each coordinate separately, after substitution from equations (9) and (10) we obtain for x-coordinate of the centre of mass of our system:
\[x_T(t)\,=\,\frac{\sum_{i=1}^2{m_ix_i(t)}}{\sum_{i=1}^2{m_i}}\,=\,\frac{m_1x_1(t)\,+\,m_2x_2(t)} {m_1\,+\,m_2}\,=\,\frac{m_1g(\sin{\alpha})t^2}{2(m_1\,+\,m_2)}\]Analogous equation for y-of the centre of mass can be obtained from equations (10) and (11):
\[y_T(t)\,=\,\frac{\sum_{i=1}^2{m_iy_i(t)}}{\sum_{i=1}^2{m_i}}\,=\,\frac{m_1y_1(t)\,+\,m_2y_2(t)} {m_1\,+\,m_2}\,=\,\frac{m_2g(\cos{\alpha})t^2}{2(m_1\,+\,m_2)}\]The coordinates of the centre of mass are changing with time in the chosen frame of reference as follow:
\[x_T(t)\,=\,\frac{m_1g(\sin{\alpha})t^2}{2(m_1\,+\,m_2)}\] \[y_T(t)\,=\,\frac{m_2g(\cos{\alpha})t^2}{2(m_1\,+\,m_2)}\] \[z_T(t)\,=\,0\]Solution - the part B
We choose a frame of reference analogously, there is only difference that the both axes are parallel with the surface of the inclined planes in distance R from it - that way we can accomplish that y-coordinate of the first ball and x-coordinate of the second ball are zero during the motion (see the figure).
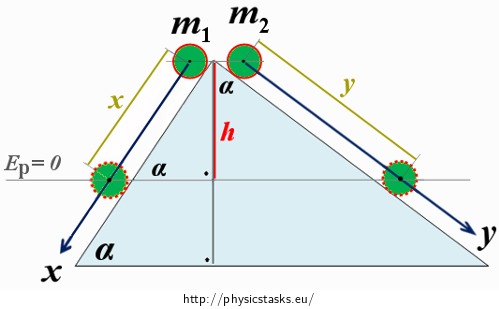
The non-zero moment of inertia J of balls will play its role, when we calculate an acceleration in each coordinate direction. Part of potential energy of ball Ep is converted into rotational kinetic energy Er during the motion on inclined plane, thus less energy can be converted into translational kinetic energy of ball Ek.The ball is moving then with smaller acceleration than in the case of neglecting the moment of inertia.
Use the law of conservation of energy to determine an acceleration of the centre of mass of balls in each coordinate direction.
We choose two situations and describe whole mechanic energy the balls have. The reference point of zero potential energy is set in depthhbelow the point of the release (see the figure above).
For the ball of mass m1:
Situation 1 – moment of release:
\[E_1\,=\,E_{p1}\tag{13}\]where Ep1 is potential energy of the ball of mass m1.
Situation 2 – the centre of mass of the ball covered a distance x:
\[E_2\,=\,E_{r1}\,+\,E_{k1}\tag{14}\]where Er1is rotational kinetic energy of the ball of mass m1 respect to axis passing through its centre and Ek1 is translational kinetic energy.
According the law of conservation of mechanical energy there holds:
\[E_1\,=\,E_2\tag{15}\]Thus, after substitution from terms (13) and (14):
\[E_{p1}\,=\,E_{r1}\,+\,E_{k1}\tag{16}\]From well-known equations for calculating the each energy we substitute in term (16):
\[m_1gh\,=\,\frac{1}{2}m_1v^2_x\,+\,\frac{1}{2}J{\omega_1}^2\tag{17}\]where vx is velocity of the centre of mass of ball, J is the moment of inertia about an axis through ball’s centre and ω1 is its angular velocity.
For the moment of inertia of the homogeneous ball of mass m1 and radius R about an axis through its centre:
\[J\,=\,\frac{2}{5}m_1R^2\tag{18}\]The figure shows that:
\[\sin{\alpha}\,=\,\frac{h}{x}\,\Rightarrow\,h\,=\,x\sin{\alpha}\tag{19}\]The magnitude of the acceleration of the centre of mass of the first ball is denoted by ax. By equations of uniformly accelerated linear motion we obtain:
\[x\,=\,\frac{1}{2}a_xt^2\tag{20}\] \[v_x\,=\,a_xt\tag{21}\]And due to property of rotational motion with angular velocity ω1:
\[\omega_1\,=\,\frac{v_x}{R}\tag{22}\]The formulae (18) to (22) substituting into equation (17) give:
\[m_1g{\cdot}\frac{1}{2}a_xt^2\sin{\alpha}\,=\,\frac{1}{2}m_1(a_xt)^2\,+\,\frac{1}{2}{\cdot}\frac{2}{5}m_1R^2{(\frac{a_xt}{R})^2}\tag{23}\]By rearranging equation (23) we obtain:
\[a_x\,=\,\frac{5}{7}g\sin{\alpha}\tag{24}\]
Analogously we can proceed also in the case of the second ball of mass m2, only the function sine is replaced by function cosine in the calculation of the hight h.
For the ball of mass m2:
The law of conservation of mechanic energy have this form:
\[E_{p2}\,=\,E_{r2}\,+\,E_{k2}\tag{25}\]where Ep2 is potential energy of the ball of mass m2, Er2 is kinetic energy of rotational motion of the ball about an axis passing though its centre and Ek2 kinetic energy of its rectilinear motion. The potential energy is calculated in the moment of release, both kinetic energies after covering the length y(analogously as in the case of the first ball).From well-known equations for calculating the each energy we substitute in term (25):
\[m_2gh\,=\,\frac{1}{2}m_2v^2_y\,+\,\frac{1}{2}J{\omega_2}^2\tag{26}\]where vy is the velocity of the centre of mass of the ball, J is the moment of inertia about an axis through ball’s centre and a ω2 is its angular velocity.
The moment of inertia of the second ball we determine the same way as we did in the case of the first ball with help of formula (18) (with mass m2), of course), the geometry of the task changes to:
\[\cos{\alpha}\,=\,\frac{h}{y}\,\Rightarrow\,h\,=\,y\cos{\alpha}\tag{27}\]A magnitude of acceleration of the centre of mass of the second ball is denotes by ay. By equations of uniformly accelerated linear motion we obtain:
\[y\,=\,\frac{1}{2}a_yt^2\tag{28}\] \[v_y\,=\,a_yt\tag{29}\]And due to property of rotational motion with angular velocity ω2:
\[\omega_2\,=\,\frac{v_y}{R}\tag{30}\]formulae (27) to (30) substituting into equation (26) give:
\[m_2g{\cdot}\frac{1}{2}a_yt^2\cos{\alpha}\,=\,\frac{1}{2}m_2(a_yt)^2\,+\,\frac{1}{2}{\cdot}\frac{2}{5}m_2R^2{(\frac{a_yt}{R})^2}\tag{31}\]By rearranging equation (31) we obtain:
\[a_y\,=\,\frac{5}{7}g\cos{\alpha}\tag{32}\]
In the next section we repeat the same technique as described in hints (5) and (6), only with different magnitudes of accelerations:
The centre of mass of the ball of mass m1 undergoes uniformly accelerated motion in the direction of the x axis and with the acceleration ax:
\[x_1´(t)\,=\,\frac{1}{2}a_xt^2\,=\,\frac{5}{14}g(\sin{\alpha})t^2\]The coordinate of the ball in the direction of y axis is identically equal to zero:
\[y_1´(t)\,=\,0\]The centre of mass of the ball of mass m2 uniformly accelerated motion in the direction of the y axis and with the acceleration ay:
\[y_2´(t)\,=\,\frac{1}{2}a_yt^2\,=\,\frac{5}{14}g(\cos{\alpha})t^2\]The coordinate of the ball in the direction of x axis is identically equal to zero:
\[x_2´(t)\,=\,0\]The coordinates of the centre of mass of the system can be calculated for each coordinate separately:
\[x_T´(t)\,=\,\frac{\sum_{i=1}^2{m_ix_i´(t)}}{\sum_{i=1}^2{m_i}}\,=\,\frac{m_1x_1´(t)\,+\,m_2x_2´(t)} {m_1\,+\,m_2}\,=\,\frac{5m_1g(\sin{\alpha})t^2}{14(m_1\,+\,m_2)}\] \[y_T´(t)\,=\,\frac{\sum_{i=1}^2{m_iy_i´(t)}}{\sum_{i=1}^2{m_i}}\,=\,\frac{m_1y_1´(t)\,+\,m_2y_2´(t)} {m_1\,+\,m_2}\,=\,\frac{5m_2g(\cos{\alpha})t^2}{14(m_1\,+\,m_2)}\]The coordinates of the centre of mass are changing with time in the chosen frame of reference as follow:
\[x_T´(t)\,=\,\frac{5m_1g(\sin{\alpha})t^2}{14(m_1\,+\,m_2)}\] \[y_T´(t)\,=\,\frac{5m_2g(\cos{\alpha})t^2}{14(m_1\,+\,m_2)}\] \[z_T´(t)\,=\,0\]Answer
Part A: (We neglect the moment of inertia of balls.)
The coordinates of the centre of mass are changing with time in the chosen frame of reference as follow:
\[x_T(t)\,=\,\frac{m_1g(\sin{\alpha})t^2}{2(m_1\,+\,m_2)}\] \[y_T(t)\,=\,\frac{m_2g(\cos{\alpha})t^2}{2(m_1\,+\,m_2)}\] \[z_T(t)\,=\,konst.\]
Part B: (We include the moment of inertia of balls.)
The coordinates of the centre of mass are changing with time in the chosen frame of reference as follow:
\[x_T´(t)\,=\,\frac{5m_1g(\sin{\alpha})t^2}{14(m_1\,+\,m_2)}\] \[y_T´(t)\,=\,\frac{5m_2g(\cos{\alpha})t^2}{14(m_1\,+\,m_2)}\] \[z_T´(t)\,=\,konst.\]Commentary 2
The solution makes sense only for such t until the one of the balls touches the horizontal surface.


