A sledge on a snow-covered hillside
Task number: 381
A boy drags a sledge along a snow-covered hillside with gradient β. The string with which he pulls his sledge makes an angle α with the plane of the hillside. Find the value of the angle α for which the force expended pulling the sledge will be minimal. The coefficient of friction between the snow and the sledge is f = 0.1. Assume constant velocity.
Analysis
We would like to determine the angle α between the string and the hillside when the force expended dragging the sledge will be minimal.
First we should find out the dependence of the tension force on the angle α (T = T(α)).
We know the sledge moves with constant speed. What is the acceleration of this sledge?
While expressing the friction force, be aware that the string is not perpendicular to the hillside. There is an angle α between them and this fact will influence the magnitude of the normal force pushing the sledge perpendicular on the hillside.
Hint 1 – Forces acting on the sledge, a force equation, the sledge’s acceleration
Draw a free body diagram of the sledge. Write a force equation for the sledge. Be aware of the acceleration of a constant velocity.
Hint 2 – Breaking the force equation into perpendicular components
We need to find out a scalar version of the force equation. Let’s establish a suitable system of coordinates. Determine force projections to the established directions and rewrite the force equations in these new directions.
Hint 3 - friction
Consider what the magnitude of the friction is depending on and formulate the equation for the friction.
Hint 4 – tension force
Insert the friction from equation (4) into equation (2) and express from it the tension force T.
Hint 5 – the angle alpha
We are looking for the angle α where the tension force is minimal. So we have to find a minimum of the function \(T(\alpha)=\frac{W(\sin\beta+f\cos\beta)}{f\sin\alpha+\cos\alpha}\), where \(T(\alpha)\) is the function T with α as a variable. We equate the derivative to zero. To be sure that we find a minimum we have to find out if the second derivative at a given angle is larger than zero.
Complete solution
Let’s draw a free body diagram of the sledge and write a force equation for it.
Forces acting on the sledge
\(\vec{W}\)… the weight
\(\vec{N}\)… the normal force of the hillside acting on the sledge
\(\vec{T}\)… the tension force by which the boy drags the sledge uphill
\(\vec{F}_{f}\)… the friction force (determines the braking of the sledge)
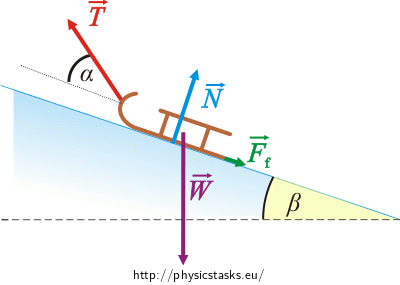
A force equation for the sledge:
\[ \vec{W}+ \vec{N} + \vec{T} + \vec{F}_{f} = m\vec{a} = 0 \tag{1}\]m… the mass of the sledge
\(\vec{a}\)… the acceleration of the sledge
The acceleration of the sledge
Because the velocity \(\vec{v}\) is constant, the acceleration \(\vec{a}\) is zero and so the net force acting on the sledge is zero, too.
To rewrite the force equation in coordinates we establish an x, y system of coordinates as follows: an axis x is identical with the direction of the sledge’s motion and an axis y is perpendicular to x.
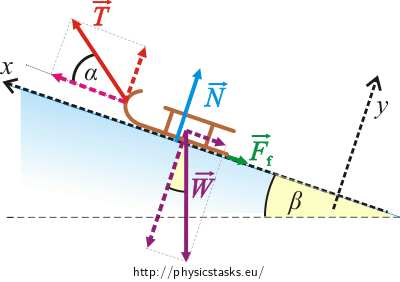
The weight \(\vec{W}\) and the tension force \(\vec{T}\) should be resolved into x, y components:
\[W_x=W\sin\beta\] \[W_y=W\cos\beta\] \[T_x=T\cos\alpha\] \[T_y=T\sin\alpha\]The force equation in the x direction:
\[ T\cos\alpha - W\sin\beta -F_{f} = 0 \tag{2}\]The force equation in the y direction:
\[ T\sin\alpha + N - W\cos\beta = 0 \tag{3}\]Friction:
Friction acting on the sledge is proportional to the normal force by with the sledge acts on the hillside. This force is, according to Newton’s third law (the law of reciprocal actions) the same magnitude as the force by which the hillside acts on the sledge. Let’s formulate the equation:
\[F_f=fN\]The force N could be expressed from equation (3) as
\[N=W\cos\beta-T\sin\alpha\]For the friction we get an equation:
\[F_f=f(W\cos\beta-T\sin\alpha)\tag{4}\]Tension force:
Let’s insert the friction from (4) into equation (2) and express the tension force T.
\[T\cos\alpha - W\sin\beta - f(W\cos\beta-T\sin\alpha)= 0 \] \[T\cos\alpha - W\sin\beta +f T\sin\alpha - fW\cos\beta= 0\] \[T\cos\alpha+f T\sin\alpha=W\sin\beta+fW\cos\beta\] \[T(f\sin\alpha+\cos\alpha)=W(\sin\beta+f\cos\beta)\] \[T=\frac{W(\sin\beta+f\cos\beta)}{f\sin\alpha+\cos\alpha}\tag{5}\]The function T(α) shows how the force T changes with as the angle α changes. We find the minimum of the function T(α) from the derivative of it with respect to a variable α. We equate the derivative to zero. To be sure that we find a minimum we have to find out if the second derivative at a given angle is larger than zero.
\[\frac{dT}{d\alpha}= \frac{d}{d\alpha}\left[\frac{W(\sin\beta+f\cos\beta)}{f\sin\alpha+\cos\alpha}\right]\] \[\frac{dT}{d\alpha}= W(\sin\beta+f\cos\beta)\frac{d}{d\alpha}\left(\frac{1}{f\sin\alpha+\cos\alpha}\right)\] \[\frac{dT}{d\alpha}= W(\sin\beta+f\cos\beta)\frac{-(f\cos\alpha-\sin\alpha)} {(f\sin\alpha+\cos\alpha)^2}\]For this equation to equal zero, the numerator on right side has to equal zero. And because the multiplicand W(sinβ+fcosβ)≠ 0, so the term (fcosα-sinα) must equal zero.
\[-f\cos\alpha+\sin\alpha=0\] \[\sin\alpha=f\cos\alpha\] \[\tan\alpha=f\] \[\alpha=\arctan f\tag{6}\]Let’s substitute the numerical value for α from equation (6).
\[\alpha=\arctan\,0.1=5^{\circ}43'\]Verify that it is the minimum of the given function.
\[\frac{d^2T}{d\alpha^2}= -W(\sin\beta+f\cos\beta)\frac{d}{d\alpha}[\frac{f\cos\alpha-\sin\alpha} {(f\sin\alpha+\cos\alpha)^2}]\] \[\frac{d^2T}{d\alpha^2}=-W(\sin\beta+f\cos\beta)\] \[\frac{(-f\sin\alpha-\cos\alpha)(f\sin\alpha+\cos\alpha)^2- 2(f\sin\alpha+\cos\alpha)(f\cos\alpha-\sin\alpha)^2} {(f\sin\alpha+\cos\alpha)^4}\] \[\frac{d^2T}{d\alpha^2}=-W(\sin\beta+f\cos\beta)\] \[\frac{-(f\sin\alpha+\cos\alpha)^3-2(f\sin\alpha+\cos\alpha)(f\cos\alpha-\sin\alpha)^2} {(f\sin\alpha+\cos\alpha)^4}\] \[\frac{d^2T}{d\alpha^2}=W(\sin\beta+f\cos\beta) \frac{(f\sin\alpha+\cos\alpha)^2+2(f\cos\alpha-\sin\alpha)^2} {(f\sin\alpha+\cos\alpha)^3}\gt 0\]The angles α and β are less than 90°, so all sines and cosines and also the entire term must be bigger than zero. Thus it is proved that we have really found the right angle, so T(α = 5°43′) is really minimal.
Complete answer
The value of angle α for which the force expended pulling the sledge will be minimal equals
\[\alpha=\arctan f=5^{\circ}43'\] .




