The Venturi Tube
Task number: 1162
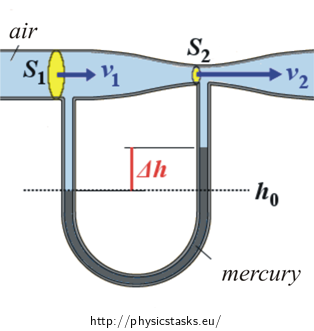
The air of velocity 15 m/s and of density 1.3 kg/m3 is entering the Venturi tube (placed in the horizontal position) from the left. The radius of the wide part of the tube is 1.0 cm; the radius of the thin part of the tube is 0.5 cm. The tube of shape U connecting wide and thin part of the main tube (see the picture) is filled with the mercury of the density 13 600 kg/m3. Determine the height difference that stabilizes between the surfaces of the mercury in U-tube.
Notation
v1 = 15 m/s Velocity of the entering air r1 = 1.0 cm Radius of the wide part of the tube r2 = 0.5 cm Radius of the thin part of the tube ρ1 = 1.3 kg/m3 Density of air ρ2 = 13 600 kg/m3 Density of the mercury Δh = ? Height difference of the surfaces in U-tube Hint 1
What causes different heights of mercury in the arms of the U-tube?
Hint 2
Can you interconnect mathematically the separate air pressure in the arms of the U-tube with the found difference Δh? Examine the size of the pressure in the lower level of the surface h0.
Hint 3
Now we will determine the pressure differences in the numerator of expression (2). Express it from Bernoulli’s principle which describes the steady flow in the main tube, and substitute it into relation for Δh.
Hint 4
What quantity from relation (5) do we have to find out yet? Use the equation which describes steady flow fluid and the quantity which we are looking for will be found in the equation. Express this quantity and substitute it into relation (5).
Complete solution
The cause of height differences is the separate air pressure above its surface. In the left arm the pressure air p1 is higher and is pushing the mercury lower into the tube. On to the contrary the pressure air p2 is lower in the right arm and the mercury can rise higher. Because the arms of the U-tube represent communicating vessels, sum the hydrostatic pressure and the pressure of air in both arms must be equal in low level of surface h0. Thus:
\[p_1\,=\,p_2\,+\,p_h\tag{1}\]where p1, p2 are air pressures in the arms of the U-tube and ph ph the hydrostatic pressure of the mercury column of height Δh. We substitute the known formula for the magnitude of the hydrostatic pressure into the equation (1) express found difference Δh:
\[p_1\,=\,p_2\,+\,{\Delta}h\varrho_2g\,\Rightarrow\,{\Delta}h\,=\,\frac{p_1\,-\,p_2}{\varrho_2g}\tag{2}\]where ρ2 is the density of the mercury and g is the gravitational acceleration.
Now your task is to express the difference of the pressure in the numerator in relation (2). Use Bernoulli’s principle which for steady flow in the Venturi tube has this form:
\[p_1\,+\,\frac{1}{2}{\varrho}_1v_1^2\,=\,p_2\,+\,\frac{1}{2}{\varrho}_1v_2^2\tag{3}\]Where the left size of the equation describes the place of the radius of tube S1 and the right size of the radius of tube S2. At the same time v1, v2 are the velocities of the air flowing in these places, and ρ1 is the density of the air. (Because the tubes are in the horizontal position, we don’t have to take in consideration the changes of the potential energy of the flowing air in Bernoulli’s principle.) It is given for the found difference of the pressure:
\[p_1\,-\,p_2\,=\,\frac{1}{2}{\varrho}_1(v_2^2\,-\,v_1^2)\tag{4}\]Substituting this relation into equation (2) we get:
\[{\Delta}h\,=\,\frac{{\varrho}_1(v_2^2\,-\,v_1^2)}{2{\varrho}_2g}\tag{5}\]The last unknown quantity in relation (5) is the velocity of air v2 at the point of radius S2. We use the continuity equation for steady flow to determine this velocity:
\[S_1v_1\,=\,S_2v_2\tag{6}\]Assume the circular radius of the tube, so you can substitute for the surfaces S1, S2 and express the velocity v2:
\[{\pi}r_1^2v_1\,=\,{\pi}r_2^2v_2\,\Rightarrow\,v_2\,=\,v_1\frac{r_1^2}{r_2^2}\tag{7}\]where r1, r2 are assigned radiuses of corresponding parts of the tube. Now substitute the calculated velocity into relation (5) and we get:
\[{\Delta}h\,=\,\frac{{\varrho}_1}{2{\varrho}_2g}((v_1\frac{r_1^2}{r_2^2})^2\,-\,v_1^2)\,=\,\frac{{\varrho}_1v_1^2}{2{\varrho}_2g}(\frac{r_1^4}{r_2^4}\,-\,1)\tag{8}\]Numerically:
\[{\Delta}h\,=\,\frac{1.3{\cdot}15^2}{2{\cdot}13\,600{\cdot}9.81}(\frac{0.010^4}{0.005^4}\,-\,1)\,\mathrm{m}\,=\,0.016\,\mathrm{m}\,=\,1.6\,\mathrm{cm}\]The difference between the levels of height of mercury in arms of U-tube is approximately 1.6 cm.
Answer
\[{\Delta}h\,=\,\frac{{\varrho}_1v_1^2}{2{\varrho}_2g}(\frac{r_1^4}{r_2^4}\,-\,1)\]Difference between the heights of the surfaces of mercury in the arms of U-tube is approximately 1.6 cm.
Using the Venturi tube
In practise the Venturi tube is used in planes to measure the flight velocity. It provides more exact measurement than for example the common Pitot tube but it is intended rather for smaller flight velocities – the speed of sound is reached in the thinner part at small velocities.


