Moving Boat
Task number: 1987
A boat sails on a river against its current from point A to point B and back to point A again. The velocity of the boat in relation to water is identical in both cases and is equal to 4 km·h−1. The velocity of the current is 1.6 km·h−1. Determine the ratio of the time the boat takes to sail from point A to point B and back and the time it would take the boat to cover the same distance on a still lake.
Given values
v = 4 km·h−1 velocity of the boat in relation to water r = 1.6 km·h−1 velocity of the current t time it takes the boat to sail from point A to point B and back t´ time it takes the boat to cover the same distance on a still lake \(\frac{t}{t^,}\,=\,\mathrm{?}\) Hint 1: Velocity of the boat sailing from A to B
Draw a free body diagram for sailing against the current and mark both velocities into it.
What is the velocity of the boat in relation to the shore when it sails against the current? Is it smaller or greater than when the boat sails on still water? How big is the difference? How long will it take the boat to cover the distance from A to B with this velocity?
Hint 2: Velocity of the boat sailing from B to A
Draw a free body diagram for sailing with the current and mark both velocities into it.
What is the velocity of the boat in relation to the shore when it sails with the current? How long will it take the boat to travel the distance from B to A with this velocity? What is the total duration of the journey?
Hint 3: Time ratio
The time the boat needs to cover the distance 2AB on still water with velocity v, as well as the ratio of both times, can be easily determined.
Overall solution
Let us assume the distance AB is equal to s km.
Fig.1 (against the current):
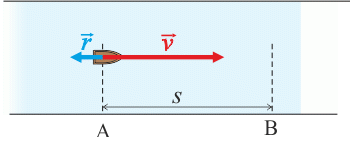
The velocity of the boat against the current in relation to the shore is equal to the difference of the boat velocity in relation to water and the velocity of the current, that is:
\[v_1\,=\,v-r\,.\]Fig. 2 (with the current):
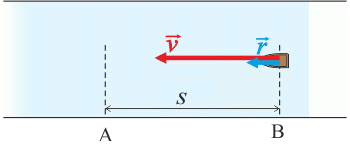
Velocity of the boat in relation to the shore is given by the sum of both velocities:
\[v_2\,=\,v+r\,.\]The boat will travel the distance s against the current in time:
\[t_1\,=\,\frac{s}{v_1}\,=\,\frac{s}{v-r}\,.\]and with the current in time:
\[t_2\,=\,\frac{s}{v_2}\,=\,\frac{s}{v+r}\,.\]The boat gets from point A to point B and back in time t:
\[t\,=\,t_1+t_2\,=\,\frac{s}{v-r}+\frac{s}{v+r}\,=\,s\,\left(\frac{1}{v-r}+\frac{1}{v+r}\right)\,=\,\frac{2v}{v^{2}-r^{2}}\,s\,.\]On a still lake, the boat sailing with velocity v would cover the distance 2AB in time t':
\[t^{,}\,=\,\frac{s}{v}+\frac{s}{v}\,=\,\frac{2}{v}\,s\,.\]We determine the ratio t/t':
\[\frac{t}{t^{,}}\,=\,\frac{\frac{2v}{v^{2}-r^{2}}\,s}{\frac{2}{v}\,s}\,=\,\frac{v^{2}}{v^{2}-r^{2}}\,=\,\frac{1}{1-\frac{r^{2}}{v^{2}}}\,.\]Numerically:
\[\frac{t}{t^{,}}\,=\,\frac{4^{2}}{4^{2}-1.6^{2}}\,=\,\frac{16}{13.44}\,\dot=\,1.19\,.\]Answer
The ratio of time t it takes the boat to sail from point A to point B and back on a river , and time t' the boat would need to sail the same distance on a still lake is:
\[\frac{t}{t^{,}}\,=\,\frac{\frac{2v}{v^{2}-r^{2}}\,s}{\frac{2}{v}\,s}\,=\,\frac{v^{2}}{v^{2}-r^{2}}\,=\,\frac{1}{1-\frac{r^{2}}{v^{2}}}\,.\]Numerically:
\[\frac{t}{t^{,}}\,=\,\frac{4^{2}}{4^{2}-1.6^{2}}\,=\,\frac{16}{13.44}\,\dot=\,1.19\,.\]



