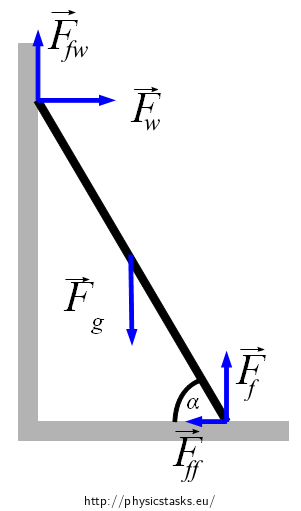
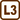A leaning ladder
Task number: 654
Hint 1
Which forces affect the ladder? Draw the forces into the picture.Hint 2
What does the fact that the ladder is at rest and does not slip down imply for the forces which affect the ladder?Hint 3
Write equations of equilibrium and rewrite them to scalar form.Hint 4
Realise what holds for the magnitude of the static friction Fff and Ffw if we are to determine the minimum angle when the ladder will have not slipped down yet.Hint 5
Substitute the equation for the friction force into (1), (2) and (3) and express from them the sought angle α.Answer
The following holds for the found angle:
\[\tan\alpha=\frac{1- \mu_{sw}\mu_{sf}}{2\mu_{sf}}\]Numerically:
\[\alpha\, \dot=\, 48^{\circ}\]Complete solution
We draw a picture, mark affecting forces and choose the coordinate system.
The affecting forces keep the ladder in balance. It means that the resultant force affecting the ladder has to equal zero as well as the resultant moment of the forces has to equal zero, too (due to a random point).
The resultant force equals zero: \(\vec{F}_g + \vec{F}_f + \vec{F}_w + \vec{F}_{ff}+ \vec{F}_{fw} = \vec{0}\)
We choose the appropriate coordinate system according to the picture and then rewrite to the scalar form:
\[x:\hspace{25px}F_w-F_{ff}=0\tag{1}\] \[y:\hspace{25px}F_f+ F_{fw} - F_g =0\tag{2}\]The resultant moment of the forces about the random point equals zero:
\[\vec{M}_g+\vec{M}_{f} +\vec{M}_w+\vec{M}_{ff} +\vec{M}_{fw}=\vec{0}\]We will determine the moment of force (Torque) for example about the centre of mass. It implies: \(\vec{M}_g=\vec{0}.\)
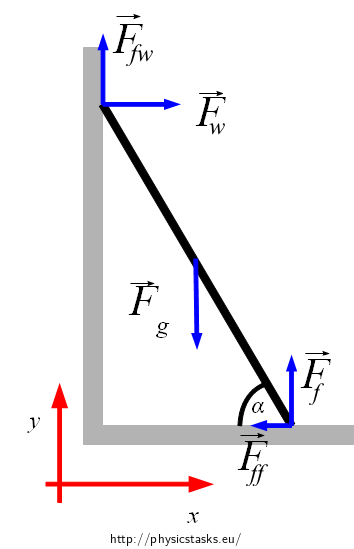
Let us remember the expression for the moment of force \(\vec{F}\) about the point O:
\[\vec{M} = \vec{r} \times \vec{F}\]The following holds for the magnitude of the moment: \(M = rF\sin \varphi\) where \(\varphi\) is the angle which is formed by vectors \(\vec{r}\) and \(\vec{F}\).
The direction of the moment of force is perpendicular to the flat surface where the vectors \(\vec{r}\) and \(\vec{F}\) lie. The orientation is determined by the Right Hand Rule: we place the fingers of the right hand to direct from \(\vec{r}\) to \(\vec{F}\) the tight thumb points to the vector \(\vec{M}\).
We choose a clockwise direction for the negative direction of the rotation, we will mark the moment of the force directing backwards from the picture with the negative sign. Then
\[M_f-M_w-M_{ff}-M_{fw}=0\]The following holds for the magnitude of the moment:
\[ \frac{L}{2}F_f\sin(90^{\circ}-\alpha)-\frac{L}{2}F_{ff}\sin\alpha - \frac{L}{2}F_w \sin \alpha- \frac{L}{2}F_{fw}\sin(90^{\circ}-\alpha)=0\]We divide L/2 and adjust:
\[ F_w \sin \alpha + F_{ff}\sin\alpha +F_{fw}\cos\alpha=F_f\cos\alpha\tag{(3)}\]For the limit angle α it holds that static friction force reaches the maximum value.
\[F_{ff}=F_f \mu_{sf}\tag{(4)}\] \[F_{fw}=F_w \mu_{sw}\tag{(5)}\] We substitute and express.From (1):
\[F_{ff}=F_w\]Substitute into equation (3):
\[F_w \sin \alpha + F_{fw} \cos \alpha + F_w \sin \alpha = F_f \cos \alpha\tag{(6)}\]According to (4) and (5):
\[F_w=F_f \mu_{sf}\] \[F_{fw}=F_w \mu_{sw} = F_f \mu_{sw} \mu_{sf}\]Substitute into equation (6):
\[F_f \mu_{sf}\sin\alpha+F_f \mu_{sw} \mu_{sf} \cos\alpha+F_f \mu_{sf}\sin\alpha=F_f\cos\alpha \]The magnitude Ff does not equal zero and therefore we can divide:
\[\mu_{sf}\sin\alpha+\mu_{sw} \mu_{sf}\cos\alpha+\mu_{sf}\sin\alpha=\cos\alpha\]We add the members of functions sine and cosine:
\[2\mu_{sf}\sin\alpha=(1-\mu_{sw} \mu_{sf})\cos\alpha\]We adjust the equation so that on one side there is an article with α and on the other side there is the rest. We divide both sides by the expression 2μsf cosα.
\[\frac{\sin\alpha}{\cos\alpha}=\frac{1-\mu_{sw} \mu_{sf}}{2\mu_{sf}}\]We get the resultant:
\[\tan\alpha=\frac{1-\mu_{sw} \mu_{sf}}{2\mu_{sf}}.\]For the given numerical values we get:
\[\tan\alpha=\frac{1- 0.3{\cdot}0.4}{2{\cdot}0.4} = 1.1\] \[\alpha\, \dot{=}\, 48^{\circ}\]