Rod on a Semi-Cylinder

Task number: 2230

A homogeneous rod of length \(2a\) is leaning on a smooth floor at point \(\mathrm{A}\) and on the surface of a semi-cylinder with a semi-circular cross-section of radius \(a\) (see figure). Friction force \(F_{fr}\) is also acting on the rod at point \(\mathrm{B}\) which prevents it from slipping.

What is its magnitude if angle between the rod and the floor is \(\alpha\)?
What is the critical angle between the rod and the floor at which the rod does not slip yet if the coefficient of friction between the rod and the cylindrical surface is \(f\)?

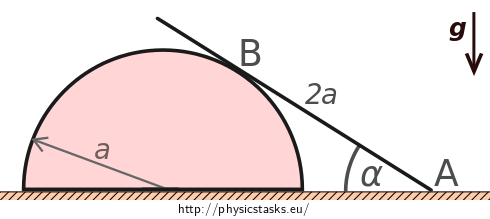
Analysis
The rod is leaning on a cylindrical surface and remains at rest. It means that the sum of forces acting on the rod, as well as their moments, must be equal to zero. Conditions of the static equilibrium of a body can be expressed by vector equations
\[\sum_{i=1}^n \vec{F_i} = \vec{0} \quad \wedge \quad \sum_{i=1}^n \vec{M_i} = \vec{0}. \tag{i}\] Moment \(\vec{M_i}\) of force \(\vec{F_i}\) is determined by the vector product \[\vec{M_i} = \vec{r_i}\times \vec{F_i},\] where \(\vec{r_i}\) is a vector, whose initial point can be chosen arbitrarily, whereas the end point corresponds with the point of application of force \(\vec{F_i}\).
Since all forces lie in one plane, the resultant vector products representing moments of these forces will lie in one straight line.

The floor is said to be smooth, which means that friction at point \(\mathrm{A}\) can be neglected.

Friction force between the rod and the cylindrical surface counterbalances the force that is trying to slip the rod off. If this force increases, the friction force will increase as well until it reaches the maximum value of static friction which is determined by the coefficient of static friction \(f\) and normal force \(N\) in the following relation
\[F{_{fr}}_\mathrm{max} = f N,\] \[ \mathrm{i.e.}\quad F_{fr} \le f N.\tag{ii}\]
In this task we want to determine the critical angle at which the rod does not yet fall, i.e. we need to find the angle at which the corresponding friction force necessary to maintain equilibrium satisfies equation (ii).

Notation

\(a\)	radius of the semi-cylindrical surface
\(2a\)	length of the homogeneous rod
\(\alpha\)	angle between the rod and the floor
\(f\)	coefficient of static friction at point \(\mathrm{B}\)

\(F_{fr} = \mathrm{?}\)	magnitude of the friction force at point \(\mathrm{B}\)
\(\alpha^\prime = \mathrm{?}\)	critical angle for the given coefficient of friction \(f\)

Hint 1: Forces Acting on the Rod
Draw all the forces acting on the rod.

Be sure to correctly determine the points of application. When considering weight, keep in mind that the rod is homogeneous. Aside from friction and weight, do not forget that both the floor and the cylinder are acting on the rod as well.
Solution of Hint 1
Forces acting on the rod
- Since the rod is homogeneous, origin of weight \(\vec{F_G}\) lies in its centre of gravity, which also corresponds to the geometric centre of the rod. Weight is directed vertically downwards. Weight is directed vertically downwards.
- Friction force \(\vec{F_{fr}}\) is originated at the point of contact of the rod and cylindrical surface and acts in tangential direction, opposite to the direction of intended motion of the rod.
- At the points of contact of the rod with the floor and cylindrical surface, reaction forces \(\vec{R_1}\) and \(\vec{R_2}\) act on the rod in the direction normal to the respective surfaces.
Hint 2: Introducing a Coordinate System
Try to introduce a suitable Cartesian coordinate system \({Oxy}\).
Solution of Hint 2
Introducing a Cartesian coordinate system \(Oxy\)
Coordinate system can be implemented in accordance with the following figure.
Hint 3: Equilibrium Conditions
Knowing that the rod is at rest, i.e. it does not move or rotate, what is the resultant force and the resultant moment of forces acting on the rod equal to?

Write down the vector equations describing conditions of static equilibrium.
Solution of Hint 3
The rod is not accelerated in any direction; therefore, the resultant force acting on the rod must be equal zero. Then
\[\vec{F_{fr}\,}+\vec{F_G} + \vec{R_1} + \vec{R_2} = \vec{0}.\tag{1}\]
The rod does not rotate, therefore the resultant moment of forces acting on the rod must equal zero. Equation of moments with respect to point \(\mathrm{A}\) is as follows:
\[\overset{\longrightarrow}{\mathrm{AB}}\times\vec{F_{fr}\,} + \overset{\longrightarrow}{\mathrm{AS}}\times\vec{F_G} + \vec{0}\times\vec{R_1} + \overset{\longrightarrow}{\mathrm{AB}}\times\vec{R_2} = \vec{0}.\tag{2}\]
Hint 4: Scalar Equations, Friction Force
Rewrite the vector equations into the scalar form. From the resulting system of three scalar equations of three unknowns, express the unknown frictional force \(F_{fr}\).
Solution of Hint 4
Decomposition of forces into x and y components

Coordinates of the components of forces in the coordinate system \(Oxy\) are shown in the figure: \[\vec{F_{fr}\,} = \left(-F_{fr}\cos{\alpha}\,,\,F_{fr}\sin{\alpha} \right),\qquad \vec{F_G} = \left(0\,,\,-F_G\right),\] \[\vec{R_1} = \left(0\,,\,R_1\right), \qquad \vec{R_2} = \left(R_2\sin{\alpha}\,,\,R_2\cos{\alpha}\right).\] If we substitute vectors in equation (1), we get a vector equation \[ \left(-F_{fr}\cos{\alpha}\,,\,F_{fr}\sin{\alpha} \right) + \left(0\,,\,-F_G\right) + \left(0\,,\,R_1\right)+ \left(R_2\sin{\alpha}\,,\,R_2\cos{\alpha}\right) = (0\,,\,0), \] which contains two scalar equations for x and y components \[ \begin{eqnarray} R_2\sin\alpha - F_{fr}\cos \alpha & = & 0~, \tag{3} \\ R_1 - F_G + R_2\cos\alpha + F_{fr}\sin\alpha & = & 0~.\tag{4} \end{eqnarray} \]
The resulting vectors of all vector products in equation (2) lie in a straight line, so we could just add or subtract their magnitudes depending on their direction. Before we write a scalar equation for moments of forces, we express the magnitudes of individual vector products.
\[ \begin{eqnarray} |\overset{\longrightarrow}{AB}\times \overset{\rightarrow}{F_{fr}}| & = & |\overset{\longrightarrow}{AB}| |\overset{\rightarrow}{F_{fr}\,}|\,\sin{0}=0~,\\ |\overset{\longrightarrow}{AS}\times \overset{\rightarrow}{F_G}| & = & |\overset{\longrightarrow}{AS}| |\overset{\rightarrow}{F_G}|\,\sin{\left(90^\mathrm{\circ} - \alpha \right)}=a\,F_G\cos\alpha \quad~\odot~,\\ |\overset{\rightarrow}{\,0}\times \overset{\rightarrow}{R_1}| & =& 0~,\\ |\overset{\longrightarrow}{AB}\times \overset{\longrightarrow}{R_2}|&=& |\overset{\longrightarrow}{AB}| |\overset{\longrightarrow}{R_2}|\,\sin{90^\mathrm{\circ}}=a\,\cot{\alpha}\,R_2 {\cdot} 1 = a\, R_2\cot\alpha \quad~\otimes~. \end{eqnarray} \] The last equation has limited validity, see Note.
Magnitude of the vector product is marked by

\(\odot\) if the vector product is directed out of the picture plane,

\(\otimes\) if the vector product is directed behind the picture plane.

Depending on the orientation of the vector product, we put plus or minus in front of its magnitude. Thus, equation (2) can be transformed into the following scalar equation
\[ \begin{eqnarray} a F_G\cos\alpha - aR_2\cot\alpha & = & 0~ \qquad |\cdot {a}^{-1},\\ F_G\cos\alpha - R_2\cot\alpha & = & 0~. \tag{5} \end{eqnarray} \]
Equations (3), (4) and (5) make three equations of three unknowns \(R_1, R_2\) and \(F_{fr}\). Since we are looking only for the magnitude of the friction force, we just need to find one unknown \(F_{fr}\).

We express \(R_2\) from equation (3)
\[R_2 = F_{fr}\frac{\cos \alpha}{\sin\alpha} = F_{fr}\cot\alpha~.\tag{I}\]
and from equation (5)
\[R_2 = F_G\frac{\cos\alpha}{\cot \alpha} = F_G \sin\alpha~. \tag{II}\]
Equalizing the right side of equations (I) and (II), we obtain an equation from which we can easily express \(F_{fr}\)
\[ \begin{eqnarray} F_{fr}\cot \alpha &=& F_G \sin\alpha,\\ \quad & \Rightarrow & F_{fr} = F_G \frac{\sin\alpha}{\cot \alpha} = F_G \tan \alpha \sin\alpha. \tag{Fr} \end{eqnarray} \]
Hint 5: Critical Angle
Consider the initial situation when the rod is at rest.

Friction force at point \(\mathrm{B}\) prevents the rod from slipping. If we move the end of the rod at point \(\mathrm{A}\) to the left, angle \(\alpha\) and magnitude of the friction force at the point where the rod touches the cylindrical surface will increase. However, static friction between the rod and the surface is limited by a maximal value equal to the product of the coefficient of static friction and normal force (reaction) of the surface.

Try to determine the maximum angle \(\alpha\) at which the rod does not slip by using equation (Fr) for \(F_{fr}(\alpha)\) and equation (II) for \(R_2(\alpha)\).
Solution of Hint 5
In the solution, we assume that for the given coefficient of friction \(f\), there is a range of angles \(\alpha\) at which it is possible to lean the rod tangentially to the surface without slipping.
Magnitude of static friction is limited by its maximum value, which depends on the coefficient of static friction and normal force of the surface, i.e.
\[F_{fr} \le fR_2.\] Substituting the angle dependence of required magnitude of friction force (Fr) and the normal force (II), we obtain \[ \begin{eqnarray} F_G \tan \alpha \sin \alpha &\le& f F_G \sin \alpha\quad|\cdot {\left(F_G \sin \alpha\right)}^{-1}\\ \tan \alpha &\le& f\\ \\ & \Longrightarrow & \alpha \le \arctan f. \end{eqnarray} \] The critical angle at which the rod does not slip yet is \[\alpha' = \arctan f.\] In case of a greater angle the rod will slide off.
Note
In the Solution of Hint 3 we have determined the following condition for angle \(\alpha\).
\[ \alpha \le \arctan f. \]
That is, the rod will not slip if angle between the floor and the rod is less than \(\arctan f\).

We must not forget that this solution is based on the equations of motion for the case when there is a right angle at point \(\mathrm{B}\). And the angle at point \(\mathrm{B}\) is equal to 90° only if the rod is propped up tangentially. The smallest angle at which the rod is still tangent to the surface is shown in the following figure.

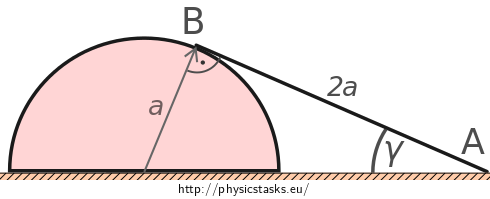
For the minimum angle \(\gamma\) at which the rod is tangent to the surface it holds true that
\[\tan \gamma = \frac{a}{2a} = \frac{1}{2} \quad \Longrightarrow \quad \gamma = \arctan\frac{1}{2} .\]
Let's clarify our conclusion. The rod will not slip if angle \(\alpha\) satisfies the following condition
\[\arctan \frac{1}{2} \le \alpha \le \arctan f.\]
It is clear from this condition that if coefficient \(f\) is not high enough, i.e.
\[\arctan f \lt \arctan \frac{1}{2},\]
there will be no tangent position of the rod at which it does not slip.

To determine what is going to happen for angle \(\alpha \lt \arctan\frac{1}{2}\), we would have to write new equations of static equilibrium.
However, it is said in the task assignment that the rod is leaning tangentially (and is not slipping). It means that there is at least one tangent position of the rod and, therefore, a critical angle at which the rod does not slip has to exist. It is given by the formula \[\alpha' = \arctan f.\] At greater angles the rod would slip.
Overall Solution
Draw all the forces acting on the rod.

Forces acting on the rod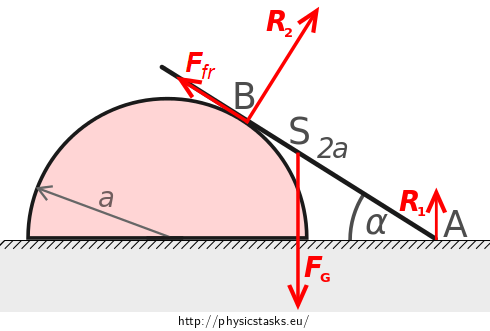
- Since the rod is homogeneous, origin of weight \(\vec{F_G}\) lies in its centre of gravity, which also corresponds to the geometric centre of the rod. Weight is directed vertically downwards. Weight is directed vertically downwards.
- Friction force \(\vec{F_{fr}}\) is originated at the point of contact of the rod and cylindrical surface and acts in tangential direction, opposite to the direction of intended motion of the rod.
- At the points of contact of the rod with the floor and cylindrical surface, reaction forces \(\vec{R_1}\) and \(\vec{R_2}\) act on the rod in the direction normal to the respective surfaces.
Introducing a Cartesian coordinate system \(Oxy\)
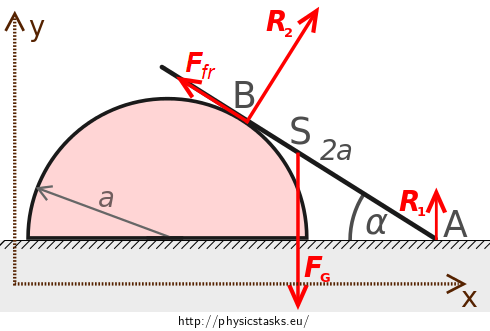
Coordinate system can be implemented in accordance with the following figure.

Equilibrium Conditions

The rod is not accelerated in any direction; therefore, the resultant force acting on the rod must be equal zero. Then
\[\vec{F_{fr}\,}+\vec{F_G} + \vec{R_1} + \vec{R_2} = \vec{0}.\tag{1}\]
The rod does not rotate, therefore the resultant moment of forces acting on the rod must equal zero. Equation of moments with respect to point \(\mathrm{A}\) is as follows:
\[\overset{\longrightarrow}{\mathrm{AB}}\times\vec{F_{fr}\,} + \overset{\longrightarrow}{\mathrm{AS}}\times\vec{F_G} + \vec{0}\times\vec{R_1} + \overset{\longrightarrow}{\mathrm{AB}}\times\vec{R_2} = \vec{0}.\tag{2}\]
Decomposition of forces into x and y components

Coordinates of the components of forces in the coordinate system \(Oxy\) are shown in the figure: \[\vec{F_{fr}\,} = \left(-F_{fr}\cos{\alpha}\,,\,F_{fr}\sin{\alpha} \right),\qquad \vec{F_G} = \left(0\,,\,-F_G\right),\] \[\vec{R_1} = \left(0\,,\,R_1\right), \qquad \vec{R_2} = \left(R_2\sin{\alpha}\,,\,R_2\cos{\alpha}\right).\] If we substitute vectors in equation (1), we get a vector equation \[ \left(-F_{fr}\cos{\alpha}\,,\,F_{fr}\sin{\alpha} \right) + \left(0\,,\,-F_G\right) + \left(0\,,\,R_1\right)+ \left(R_2\sin{\alpha}\,,\,R_2\cos{\alpha}\right) = (0\,,\,0), \] which contains two scalar equations for x and y components \[ \begin{eqnarray} R_2\sin\alpha - F_{fr}\cos \alpha & = & 0~, \tag{3} \\ R_1 - F_G + R_2\cos\alpha + F_{fr}\sin\alpha & = & 0~.\tag{4} \end{eqnarray} \]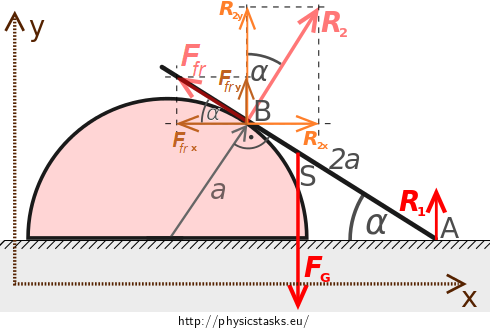
The resulting vectors of all vector products in equation (2) lie in a straight line, so we could just add or subtract their magnitudes depending on their direction. Before we write a scalar equation for moments of forces, we express the magnitudes of individual vector products.
\[ \begin{eqnarray} |\overset{\longrightarrow}{AB}\times \overset{\rightarrow}{F_{fr}}| & = & |\overset{\longrightarrow}{AB}| |\overset{\rightarrow}{F_{fr}\,}|\,\sin{0}=0~,\\ |\overset{\longrightarrow}{AS}\times \overset{\rightarrow}{F_G}| & = & |\overset{\longrightarrow}{AS}| |\overset{\rightarrow}{F_G}|\,\sin{\left(90^\mathrm{\circ} - \alpha \right)}=a\,F_G\cos\alpha \quad~\odot~,\\ |\overset{\rightarrow}{\,0}\times \overset{\rightarrow}{R_1}| & =& 0~,\\ |\overset{\longrightarrow}{AB}\times \overset{\longrightarrow}{R_2}|&=& |\overset{\longrightarrow}{AB}| |\overset{\longrightarrow}{R_2}|\,\sin{90^\mathrm{\circ}}=a\,\cot{\alpha}\,R_2 {\cdot} 1 = a\, R_2\cot\alpha \quad~\otimes~. \end{eqnarray} \] The last equation has limited validity, see Note.
Magnitude of the vector product is marked by

\(\odot\) if the vector product is directed out of the picture plane,

\(\otimes\) if the vector product is directed behind the picture plane.

Depending on the orientation of the vector product, we put plus or minus in front of its magnitude. Thus, equation (2) can be transformed into the following scalar equation
\[ \begin{eqnarray} a F_G\cos\alpha - aR_2\cot\alpha & = & 0~ \qquad |\cdot {a}^{-1},\\ F_G\cos\alpha - R_2\cot\alpha & = & 0~. \tag{5} \end{eqnarray} \]
Equations (3), (4) and (5) make three equations of three unknowns \(R_1, R_2\) and \(F_{fr}\). Since we are looking only for the magnitude of the friction force, we just need to find one unknown \(F_{fr}\).

We express \(R_2\) from equation (3)
\[R_2 = F_{fr}\frac{\cos \alpha}{\sin\alpha} = F_{fr}\cot\alpha~.\tag{I}\]
and from equation (5)
\[R_2 = F_G\frac{\cos\alpha}{\cot \alpha} = F_G \sin\alpha~. \tag{II}\]
Equalizing the right side of equations (I) and (II), we obtain an equation from which we can easily express \(F_{fr}\)
\[ \begin{eqnarray} F_{fr}\cot \alpha &=& F_G \sin\alpha,\\ \quad & \Rightarrow & F_{fr} = F_G \frac{\sin\alpha}{\cot \alpha} = F_G \tan \alpha \sin\alpha. \tag{Fr} \end{eqnarray} \]

Critical Angle
In the solution, we assume that for the given coefficient of friction \(f\), there is a range of angles \(\alpha\) at which it is possible to lean the rod tangentially to the surface without slipping.
Magnitude of static friction is limited by its maximum value, which depends on the coefficient of static friction and normal force of the surface, i.e.
\[F_{fr} \le fR_2.\] Substituting the angle dependence of required magnitude of friction force (Fr) and the normal force (II), we obtain \[ \begin{eqnarray} F_G \tan \alpha \sin \alpha &\le& f F_G \sin \alpha\quad|\cdot {\left(F_G \sin \alpha\right)}^{-1}\\ \tan \alpha &\le& f\\ \\ & \Longrightarrow & \alpha \le \arctan f. \end{eqnarray} \] The critical angle at which the rod does not slip yet is \[\alpha' = \arctan f.\] In case of a greater angle the rod will slide off.
Answer
1. Magnitude of the friction force between the rod of length \(2a\) and of the mass \(m\) which is leaning tangentially on the semi-cylindrical surface of radius \(a\) is determined by the relation \(F_{fr} = F_G \tan \alpha \sin \alpha,\)
  where \(\alpha\) is the angle that the rod makes with the horizontal plane.
2. Angle \(\alpha\) between the rod and the floor can be increased up to the critical value \(\alpha' = \arctan f\). At greater angles, the rod will slip.
Links to Similar Problems
If you have grown to like problems about a homogeneous rod leaning on various objects, or you would like to practice this type of problems, try solving one of the following equally interesting tasks:
- A Rod Leaning on a Step,
- Problém s trámem (will be translated soon).