A space probe
Task number: 512
A space probe which moves with a speed of v0 explodes during its flight and falls apart into three pieces of the same mass. One part continues flying in the original direction, while the two remaining parts fly in different directions which form an angle 60° to -60° with the original direction within the same plane. The energy released during the explosion is twice as large as the kinetic energy which the space probe had just before the explosion. Determine the magnitude of the speed and the kinetic energy of the individual pieces immediately after the explosion.
Analysis
The solution of the task uses the law of conservation of linear momentum and the law of conservation of energy.
Hint 1 - the law of conservation of linear momentum
Draw a picture and choose an appropriate coordinate system. Write the law of conservation of linear momentum for this situation.
Solution to Hint 1 - the law of conservation of energy
Write the law of conservation of energy for this particular situation. Figure out what the total energy of the space probe is before the explosion and immediately after its disintegration. Find formulas for the speeds of the individual parts.
Hint 3 – the kinetic energy of the parts of the space probe
Express the relations for the kinetic energy of the individual parts of the space probe and substitute for the corresponding speeds.
Answer
The magnitude of the speed of the first and the third part of the space probe immediately after the explosion is \(v_1=v_3=\frac{6v_0\cos\alpha}{1+2\cos^2\alpha}=2v_0\).
The magnitude of the speed of the second part of the space probe immediately after the explosion is \(v_2=\frac {3v_0(1-2\cos^2\alpha)}{1+2\cos^2\alpha}=v_0\).
The kinetic energy of the first and the third part of the space probe immediately after the explosion is \(E_{k1}=E_{k3}=6m\frac{v_0^2\cos^2\alpha}{(1+2\cos^2\alpha)^2}=\frac{2}{3}mv_0^2=\frac{4}{3}E_k.\)
The kinetic energy of the second part of the space probe immediately after the explosion is \(E_{k2}=\frac{3}{2}m\frac{v_0^2(1-\cos^2\alpha)^2}{(1+2\cos^2\alpha)^2}=\frac{mv_0^2}{6}=\frac{1}{3}E_k.\)
COMPLETE SOLUTION
The solution of the task uses the law of conservation of linear momentum and the law of conservation of energy.
Draw a picture this situation:
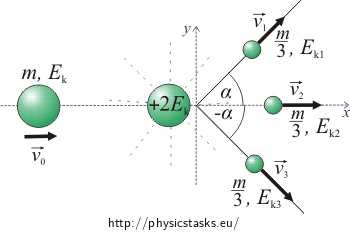
\(m\)...... the mass of the space probe
\(v_0\)...... the vector velocity of the space probe before the explosion
\(v_1\)...... the vector velocity of the first part of the space probe immediately after explosion
\(v_2\)...... the vector velocity of the second part of the space probe immediately after explosion
\(v_3\)......the vector velocity of the third part of the space probe immediately after explosion
\(\alpha\)...... the angular deviations of the first and the third part of the space probe
The coordinate system is chosen so that the x-axis has the direction in which the space probe moves before the explosion and the y-axis is perpendicular to it.
The law of conservation of linear momentum states that the total momentum of the system is preserved.
\[\vec{p}=\vec{p_1}+\vec{p_2}+\vec{p_3}\]\(\vec{p}\)...... the vector momentum of the space probe before the explosion
\(\vec{p_1}\)...... the vector momentum of the first part of the space probe immediately after the explosion
\(\vec{p_2}\)...... the vector momentum of the second part of the space probe immediately after the explosion
\(\vec{p_3}\)...... the vector momentum of the third part of the space probe immediately after the explosion
\[m\vec{v_0}=\frac{m}{3}\vec{v_1}+\frac{m}{3}\vec{v_2}+\frac{m}{3}\vec{v_3}\]Scalar form:
The projection to the x-axis:
\[mv_0=\frac{1}{3}mv_1\cos\alpha + \frac{1}{3}mv_2 + \frac{1}{3}mv_3\cos(-\alpha)\] \[cos(-\alpha)= cos\alpha\] \[mv_0=\frac{1}{3}mv_1\cos\alpha + \frac{1}{3}mv_2 + \frac{1}{3}mv_3\cos\alpha\tag{1}\]The projection to the y-axis:
\[0=\frac{1}{3}mv_1\sin\alpha + \frac{1}{3}mv_3\sin(-\alpha)\] \[sin(-\alpha)= - sin\alpha\] \[0=\frac{1}{3}mv_1\sin\alpha - \frac{1}{3}mv_3\sin\alpha\tag{2}\]From equation (2) we express the speed of the first part of the space probe \(v_1\):
\[v_1\sin\alpha=v_3\sin\alpha\] \[v_1=v_3\tag{3}\]We substitute equation (3) into equation (1):
\[mv_0=2\frac{1}{3}mv_1\cos\alpha + \frac{1}{3}mv_2\]From that we express the speed of the second part of the space probe immediately after the explosion:
\[v_2=3v_0-2v_1\cos\alpha\tag{4}\]The law of conservation of energy: the sum of the kinetic energy of the space probe before the explosion and the energy released during the explosion equals the sum of the kinetic energy of the individual parts of the space probe after the explosion.
The law of conservation of energy:\(\qquad E_k+ 2E_{k}=E_{k1}+E_{k2}+E_{k3}\)
\(E_k\)......... the starting kinetic energy of the space probe
\(2E_{k}\)...... the energy released during the explosions
\(E_{k1}\)...... the kinetic energy of the first part of the space probe immediately after the explosion
\(E_{k2}\)...... the kinetic energy of the second part of the space probe immediately after the explosion
\(E_{k3}\)...... the kinetic energy of the third part of the space probe immediately after the explosion
\[\frac{1}{2}mv_0^2+2\frac{1}{2}mv_0^2=\frac{1}{2}\frac{m}{3}v_1^2+\frac{1}{2}\frac{m}{3}v_2^2+\frac{1}{2}\frac{m}{3}v_3^2\] \[\frac{3}{2}mv_0^2=\frac{1}{6}mv_1^2+\frac{1}{6}mv_2^2+\frac{1}{6}mv_3^2\]We divide the equation by the mass m and multiply it by six:
\[9v_0^2=v_1^2+v_2^2+v_3^2\]We substitute for the speed v3 from equation (3):
\[9v_0^2=2v_1^2+v_2^2\]We substitute for the speed v2 from equation (4):
\[9v_0^2=2v_1^2+(3v_0-2v_1\cos\alpha)^2=2v_1^2+9v_0^2-12v_0v_1\cos \alpha +4v_1^2\cos ^2\alpha\]
We rearrange the equation and express the speed v1:
\[2v_1^2(1+2\cos^2 \alpha) = 12v_0v_1\cos \alpha\] \[v_1(1+2\cos^2 \alpha) = 6v_0\cos \alpha\] \[v_1=v_3=\frac{6v_0\cos \alpha}{1+2\cos^2 \alpha}\] \[\cos \alpha=\cos 60^{\circ}=\frac{1}{2}\] \[v_1=v_3=\frac{3v_0}{1+\frac{1}{2}}=2v_0\]By substitution into equation (4) we get the speed v2:
\[v_2=3v_0-\frac{12v_0\cos^2 \alpha}{1+2\cos^2 \alpha}=\frac{3v_0(1+2\cos^2 \alpha -4\cos^2 \alpha)}{1+2\cos^2 \alpha}=\frac{3v_0(1-2\cos^2 \alpha)}{1+2\cos^2 \alpha}\]
\[\cos \alpha=\cos 60^{\circ}=\frac{1}{2}\] \[v_2=\frac{3v_0(1-\frac{1}{2})}{1+\frac{1}{2}}=v_0\]Express the kinetic energy of the individual parts of the space probe and substitute for the corresponding speeds.
The kinetic energy of the first and the third part of the space probe:
\[E_{k1}=E_{k3}=\frac{1}{6}mv_1^2\] \[E_{k1}=\frac{1}{6}m\frac{36v_0^2\cos^2\alpha}{(1+2\cos^2\alpha)^2}=6mv_0^2\frac{\cos^2\alpha}{(1+2\cos^2\alpha)^2}\] \[\cos \alpha=\cos 60^{\circ}=\frac{1}{2}\] \[E_{k1}=6mv_0^2\frac{\frac{1}{4}}{(1+\frac{1}{2})^2}=\frac{6}{9}mv_0^2\] \[E_{k1}=E_{k3}=\frac{2}{3}mv_0^2=\frac{4}{3}E_k\]The kinetic energy of the second part of the space probe:
\[E_{k2}=\frac{1}{6}mv_2^2\] \[E_{k2}=\frac{1}{6}m\frac{9v_0^2(1-2\cos^2\alpha)^2}{(1+2\cos^2\alpha)^2}=3\frac{mv_0^2}{2}\frac{(1-2\cos^2\alpha)^2}{(1+2\cos^2\alpha)^2}\] \[\cos \alpha=\cos 60^{\circ}=\frac{1}{2}\] \[E_{k2}=3\frac{mv_0^2}{2}\frac{(1-\frac{1}{2})^2}{(1+\frac{1}{2})^2}=\frac{3}{2}mv_0^2\cdot\frac{4}{4{\cdot}9}\] \[E_{k2}=\frac{mv_0^2}{6}=\frac{1}{3}E_k\]Answer:
The magnitude of the speed of the first and the third part of the space probe immediately after the explosion is \(v_1=v_3=\frac{6v_0\cos\alpha}{1+2\cos^2\alpha}=2v_0\).
The magnitude of the speed of the second part of the space probe immediately after the explosion is \(v_2=\frac {3v_0(1-2\cos^2\alpha)}{1+2\cos^2\alpha}=v_0\).
The kinetic energy of the first and the third part of the space probe immediately after the explosion is \(E_{k1}=E_{k3}=6m\frac{v_0^2\cos^2\alpha}{(1+2\cos^2\alpha)^2}=\frac{2}{3}mv_0^2=\frac{4}{3}E_k.\)
The kinetic energy of the second part of the space probe immediately after the explosion is \(E_{k2}=\frac{3}{2}m\frac{v_0^2(1-\cos^2\alpha)^2}{(1+2\cos^2\alpha)^2}=\frac{mv_0^2}{6}=\frac{1}{3}E_k.\)



