Forces in a Rope
Task number: 1752
A body of mass of 20 kg is tied to a rope and rotates in a vertical plane. The radius of the rotation is 1 m.
What is the maximum and minimum force acting in the rope if the speed of the body is 10 m·s−1?
Solve this problem both with respect to an inertial frame of reference (the observer is standing on the ground) and with respect to a non-inertial frame of reference (the observer is rotating with the body).
Notation
m = 20 kg mass of the body v = 10 m·s−1 tangential speed of the body r = 1 m radius of the rotation of the body Fmax = ? magnitude of the maximum force acting in the rope Fmin = ? magnitude of the minimum force acting in the rope Hint 1 – Forces with Respect to an Inertial Frame of Reference
What forces are acting upon the body with respect to an inertial frame of reference?
What force is acting in the rope?
At what point on the trajectory of the body will the force acting in the rope be the least and at what point will it be the greatest?
Hint 2 – Forces with Respect to a Non-Inertial Frame of Reference
What forces are acting upon the body with respect to a non-inertial frame of reference centered on the body? What motion does the body perform with respect to this non-inertial frame? What holds for the net force acting upon the body?
At what point on the trajectory of the body will the force acting in the rope be the least and at what point will it be the greatest? Write the equation of motion at these points.
COMPLETE SOLUTION
This problem can be solved either with respect to an inertial frame of reference or with respect to a non-inertial frame of reference.
1. With respect to an inertial frame of reference centered on the ground
With respect to an inertial frame (centered on the ground) the body moves in a circle and is being acted upon by the gravitational force FG and the tensile force of the rope FR.
If the rope acts upon the body with the tensile force FR, then the body acts upon the rope with an equal and opposite force. The magnitude of this force is equal to the magnitude of the force FR.
Shown in the pictures are the forces at the lowest and at the highest point of the trajectory, when the forces lie on one line.
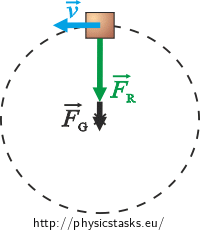
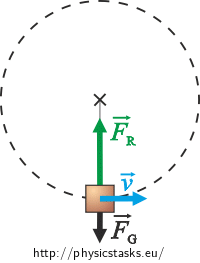
The net force Fcp of the forces at these points causes centripetal acceleration of the body.
For the magnitudes of the forces at the highest point it holds:
\[F_{cp}\,=\, F_{R} + F_{g},\] \[F_{R} \,=\, F_{cp} - F_{g} \,=\, m\frac{v^{2}}{r} - mg.\]For the magnitudes of the forces at the lowest point it holds:
\[F_{cp} \,=\, F_{R} - F_{g},\] \[F_{R} \,=\, F_{cp} + F_{g} \,=\, m\frac{v^{2}}{r} + mg.\]At the points that are on a horizontal line with the center of rotation the tension force of the rope is directly equal to the centripetal force and its magnitude is:
\[F_{R} \,=\, F_{cp} \,=\, m\frac{v^{2}}{r}.\]Therefore the rope has to pull the most at the lowest point, because the gravitational force acts against it. The rope has to pull the least at the highest point, because the gravitational force acts in the same direction.
Numerically:
Maximum tensile force – the lowest point:
\[F_{\mathrm{max}} \,=\,m\frac{v^{2}}{r}+mg\,=\,20\,\cdot\,\frac{10^{2}}{1}+20\,\cdot\,10\,\mathrm{N}\,= \, 2200\,\mathrm{N}.\]Minimum tensile force – the highest point:
\[F_{\mathrm{min}} \,=\, m\frac{v^{2}}{r}-mg\,=\,20\,\cdot\,\frac{10^{2}}{1}-20\,\cdot\,10\,\mathrm{N}\,= \,1800\,\mathrm{N}.\]We consider the gravitational acceleration to be 10 m·s−2.
2. With respect to a non-inertial frame of reference rotating with the body
If we’re watching the body with respect to a non-inertial frame, it is at rest relative to us. There are not only the gravitational force and the tensile force of the rope acting upon the body but also an inertial centrifugal force Fcf. The net force acting upon the body is zero.
If the rope acts upon the body with the tensile force FL, then the body acts upon the rope with an equal and opposite force. The magnitude of this force is equal to the magnitude of the force FL.
Shown in the pictures are the forces at the lowest and at the highest point of the trajectory, when the forces lie on one line.
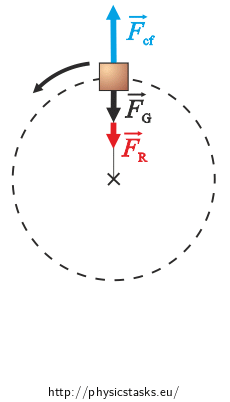
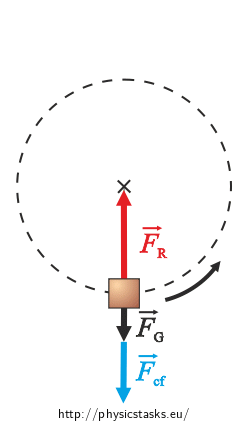
The net force at these points is zero.
For the magnitudes of the forces at the highest point it holds:
\[F_{cf} - F_{R} - F_{g}\,=\,0,\] \[F_{R} \,=\, F_{cf} - F_{g} \,=\, m\frac{v^{2}}{r} - mg.\]For the magnitudes of the forces at the lowest point it holds:
\[F_{R} - F_{cf} - F_{g} \,=\,0,\] \[F_{R} \,=\, F_{cf} + F_{g} \,=\, m\frac{v^{2}}{r} + mg.\]At the points that are on a horizontal line with the center of rotation the magnitude of the tensile force of the rope is equal to the magnitude of the inertial centrifugal force.
\[F_{R} = F_{cf} \,=\, m\frac{v^{2}}{r}.\]Therefore the rope has to pull the most at the lowest point and the least at the highest point.
Numerically:
Maximum tensile force – the lowest point:
\[F_{\mathrm{max}} \,=\,m\frac{v^{2}}{r}+mg\,=\,20\,\cdot\,\frac{10^{2}}{1}+20\,\cdot\,10\,\mathrm{N}\,= \, 2200\,\mathrm{N}.\]Minimum tensile force – the highest point:
\[F_{\mathrm{min}} \,=\, m\frac{v^{2}}{r}-mg\,=\,20\,\cdot\,\frac{10^{2}}{1}-20\,\cdot\,10\,\mathrm{N}\,= \,1800\,\mathrm{N}.\]We consider the gravitational acceleration to be 10 m·s−2.
Answer
\[F_{\mathrm{max}} \,=\,m\frac{v^{2}}{r}+mg\,=\, 2200\,\mathrm{N}\] \[F_{\mathrm{min}} \,=\,m\frac{v^{2}}{r}-mg\,=\,1800\,\mathrm{N}\]We consider the gravitational acceleration to be m·s−2.
The magnitude of the tensile force is not dependent on the frame of reference we use. The maximum tensile force is at the lowest point of the trajectory and its magnitude is 2200N. The minimum tensile force is at the highest point of the trajectory and its magnitude is 1800N.
Similar Task
The task Koule přivázaná na konci provazu (A Ball Attached to a Rope; Czech only) also shows how to calculate the tensile force acting upon a ball in a vertical plane with respect to an inertial frame of reference.


