A rolling hoop

Task number: 655

An object in a shape of a hoop with a mass 10 kg, a diameter 1 m and negligible thickness rolls without slipping on an inclined plane which forms the angle 30° with the horizontal plane. Find what speed has the centre of gravity of the hoop after covering the distance of 5 m if the initial speed of the hoop equals zero. Ignore the loss of the energy by friction.

Analysis
It is possible to solve this task in two ways: either by the law of conservation of mechanical energy (Hint marked as A) or the Impulse-momentum theorem (Hint marked as B).

In the first case it is necessary to choose two appropriate situations in which we will compare the mechanical energy of the hoop. Realise that the hoop rotates around its centre of mass and at the same time it does the translational motion.

When solving it by the impulse-momentum theorem it is necessary to consider which forces affect the hoop, what holds for their resultant of forces and for the resultant of the moment of these forces. It is also necessary to consider which point you will relate the moments of forces to and taking this into consideration write the right form for the moment of the inertia of the hoop about an axis passing through this point.
Impulse-momentum theorem and Angular momentum theorem (and something more)
Impulse-momentum theorem (as the theorem about the motion centre of mass) states that:

The centre of the mass moves like the mass point with total mass of the system which is affected by the resultant of external forces acting on the system.
\[\vec{F}_v = m_c \vec{a}\]
Angular momentum theorem:

The time change of the moment of inertia of the system equals the total moment of the external forces.
\[\vec{M}=\frac{d\vec{L}}{dt}\]
(\(\vec{M}\) and \(\vec{L}\) are related to the same point.)

In this case of the rotation of the rigid body about a fixed axis - it holds true:
\[L = I \omega\] \[\vec{M}=\frac{d\vec{L}}{dt} = I\vec{\epsilon}\]
Where:

I … moment of inertia of the object about a fixed axis

\(\vec{\epsilon}\)… angular acceleration (vectors \(\vec{\epsilon}\), \(\vec{M}\) aim in the direction the axis of rotation)

Parallel axis theorem or Huygens-Steiner theorem:
\[I = I_c + mr^2\]
Where:

I … moment of inertia of the object about the random axis o

I_c … moment of inertia of the object about the axis passing through its centre of mass (o is parallel to o_c)

m … the mass of the object

r … is the perpendicular distance between the two axes o and o_c

König’s theorem:

The total kinetic energy of a body which does the translational and rotary motion around the centre of mass
\[E_k = \frac{1}{2}mv_c^2 + \frac{1}{2}I_c\omega^2\]
Where:

v_c… speed of the centre of mass

I_c … moment of inertia of the object about an axis passing through its centre of mass
Centre of mass or centre of gravity
In the task we can read about the centre of mass (eventually the centre) and the centre of gravity. The author always has in mind the same point

In what ways are they different?

The centre of gravity is defined as a point where the location of the gravitational force acts on a body. There is no sense in mentioning it without this force.

On the contrary the centre of mass is defined mathematically. Plainly said the coordinate of the centre of mass is the average of the coordinates of all the points of a body.

Their position could be differentiated only by non-homogenous gravitational field for example if this task took place near a tiny black hole. We don’t encounter these problems in practice. (Let alone the fact that within the reach of black holes we usually have only one problem and that is how to get away as quickly as possible).
Hint 1A
Choose two situations in which you will compare the mechanical energy of the hoop. Don’t forget to choose the zero level of the potential energy.
Solution to Hint 1A

Take notice of kinetic energy E_k0 and potential E_p0 energy at the beginning of the motion and after covering the distance with E_k, E_p.

According to the law of conservation of mechanical energy it holds true that:
\[E_{k0}+E_{p0} = E_k+ E_p\]
Initial speed equals zero and therefore the kinetic energy is:
\[E_{k0}=0\]
We choose the zero level of the potential energy so that it will equal zero after covering the distance s:
\[E_p=0\]
And so:
\[E_{p0} = E_k\tag{1}\]
Hint 2A
Express the potential energy of the hoop in the situation (1) and the kinetic energy of the hoop in the situation (2). Substitute this expression into the equation (1) and express the sought speed.
Solution to Hint 2A
The following holds for the potential energy of the hoop in situation (1):
\[E_{p0}=mgh\]
Where h, difference of the height, is in this case:
\[h=s\sin\alpha\]
The kinetic energy of the hoop in situation (2) consists of two components, the energy of the rotation of the hoop abound the centre of mass and translational kinetic energy of the centre of gravity.
\[E_k=\frac{1}{2} I\omega^2+ \frac{1}{2} mv^2.\]
The moment of inertia of the hoop about an axis passing through its centre of mass is \(I=mr^2\).

The following holds for angular velocity of rotation of the hoop:
\[\omega=\frac{v}{r}.\]
We substitute them one by one into the equation (1):
\[E_{p0}=E_k\] \[mgh=\frac{1}{2} I\omega^2+ \frac{1}{2} mv^2\] \[mgs \sin\alpha= \frac{1}{2} mr^2(\frac{v}{r})^2+\frac{1}{2}mv^2\]
We divide by m and add the right hand:
\[gs \sin\alpha=v^2\] \[v=\sqrt{gs \sin\alpha}.\]
Hint 1B
Draw all forces which affect the hoop in the picture. Write what holds for their resultant.
Solution to Hint 1B
- \(\vec{F}_g\)...the weight
- \(\vec{F}_r\)...force by which the plane affects the hoop
- \(\vec{F}_f\)...friction force because the hoop doesn’t slip
The following hols for the resultant of forces:
\[\vec{F}_g + \vec{F}_f + \vec{F}_r = m\vec{a}\]
Where \(\vec{a}\) is the acceleration of the centre of gravity.

We rewrite to scalar form. We choose x-axis in the direction of the motion of the centre of the gravity and y-axis perpendicular to x-axis.
\[x: \hspace{20px} mgsin\alpha - F_f = ma\tag{2}\] \[y: \hspace{20px} F_r - mg cos\alpha = 0\]
Hint 2B
Choose a point which you’ll relate the moments of the acting forces to and write what holds for them.
Solution to Hint 2B
Due to centre of mass C:

Moments of these forces \(\vec{F}_g\) and \(\vec{F}_r\) equal zero, then:
\[\vec{M}=\vec{r}\times\vec{F}_f = I\vec{\epsilon}\]
We rewrite to scalar form:
\[F_{f}r = I\epsilon = I \frac{a}{r}\]
The following holds for moment of inertia: \(I = mr^2\), then:
\[F_fr = mr^2\frac{a}{r}\]
Where:
\[F_f = ma\tag{3}\]
Hint 3B
Express the acceleration of the hoop by equations (2) and (3) and then express the speed.
Solution to Hint 3B
We substitute from (3) for F_f into equation (2):
\[mg\sin\alpha = 2ma\]
We divide expression by m:
\[a = \frac{1}{2}g\sin\alpha\tag{4}\]
The following holds for the covered distance:
\[s=\frac{1}{2}at^2\]
Where:
\[v=at\]
Where:
\[s=\frac{1}{2}a\frac{v^2}{a^2}\] \[v^2 = 2sa\] \[v=\sqrt{2sa}\]
We substitute from (4):
\[v=\sqrt{2s\frac{1}{2}g\sin\alpha}\] \[v=\sqrt{gs\sin\alpha}\]
Note
The moment of the acting forces can be related even to a different point for example point Q where the hoop touches the plane. Therefore the moment of two forces, the friction force and the reaction of the plane (normal force) will equal zero.

The moment of gravitational force is given as
\[\vec{M}=\vec{r}\times\vec{F}_g = I_Q\vec{\epsilon}\]
We rewrite to scalar form:
\[M=F_{g}r\sin\alpha= I_Q\epsilon \] \[mgr\sin\alpha = I_Q \frac{a}{r}\]
The moment of inertia of the hoop with mass m due to the axis passing through the centre is \(I=mr^2\), obut the point of the contact is in the distance r from the axis passing through the centre, so according to Huygens-Steiner theorem:
\[I_Q=I+md^2=mr^2+mr^2=2mr^2\]
And so:
\[mgr\sin\alpha = 2mr^2\frac{a}{r}\]
Where:
\[a = \frac{1}{2}g\sin\alpha\]
The solution is onward the same as in Hint 3B.
For the given numerical values
\[\alpha=30^{\circ}\] \[sin\alpha=0.5\] \[s=5\,\mathrm{m}\] \[g=9.81\,\mathrm{ms^{-2}}\] \[v=\sqrt{gs \sin\alpha}=\sqrt{9.81{\cdot}5\cdot0.5} \,\mathrm{ms^{-1}}\dot{=}5 \,\mathrm{ms^{-1}}\]
Answer
The speed of the mass of the hoop is:
\[v=\sqrt{gs \sin\alpha}\]
Numerically:
\[v\, \dot{=}\,5 \,\mathrm{ms^{-1}} \]
Complete solution with help of the law of conservation of mechanical energy
Choose two situations in which you will compare the mechanical energy of the hoop.

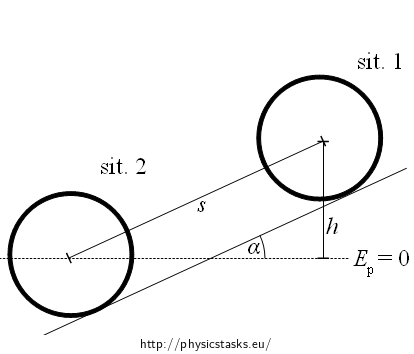
Take notice of kinetic energy E_k0 and potential E_p0 energy at the beginning of the motion and after covering the distance with E_k, E_p.

According to the law of conservation of mechanical energy it holds true that:
\[E_{k0}+E_{p0} = E_k+ E_p\]
Initial speed equals zero and therefore the kinetic energy is:
\[E_{k0}=0\]
We choose the zero level of the potential energy so that it will equal zero after covering the distance s:
\[E_p=0\]
And so:
\[E_{p0} = E_k\tag{1}\]
The following holds for the potential energy of the hoop in situation (1):
\[E_{p0}=mgh\]
Where h, difference of the height, is in this case:
\[h=s\sin\alpha\]
The kinetic energy of the hoop in situation (2) consists of two components, the energy of the rotation of the hoop abound the centre of mass and translational kinetic energy of the centre of gravity.
\[E_k=\frac{1}{2} I\omega^2+ \frac{1}{2} mv^2.\]
The moment of inertia of the hoop about an axis passing through its centre of mass is \(I=mr^2\).

The following holds for angular velocity of rotation of the hoop:
\[\omega=\frac{v}{r}.\]
We substitute them one by one into the equation (1):
\[E_{p0}=E_k\] \[mgh=\frac{1}{2} I\omega^2+ \frac{1}{2} mv^2\] \[mgs \sin\alpha= \frac{1}{2} mr^2(\frac{v}{r})^2+\frac{1}{2}mv^2\]
We divide by m and add the right hand:
\[gs \sin\alpha=v^2\] \[v=\sqrt{gs \sin\alpha}.\]
Complete solution with help of Impulse-momentum theorem
Draw all forces which affect the hoop in the picture. Write what holds for their resultant.
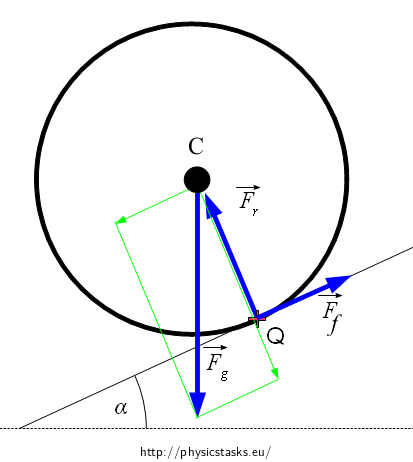
- \(\vec{F}_g\)...the weight
- \(\vec{F}_r\)...force by which the plane affects the hoop
- \(\vec{F}_f\)...friction force because the hoop doesn’t slip
The following hols for the resultant of forces:
\[\vec{F}_g + \vec{F}_f + \vec{F}_r = m\vec{a}\]
Where \(\vec{a}\) is the acceleration of the centre of gravity.

We rewrite to scalar form. We choose x-axis in the direction of the motion of the centre of the gravity and y-axis perpendicular to x-axis.
\[x: \hspace{20px} mgsin\alpha - F_f = ma\tag{1}\] \[y: \hspace{20px} F_r - mg cos\alpha = 0\]
Choose a point which you’ll relate the moments of the acting forces to and write what holds for them.

Due to centre of mass C:

Moments of these forces \(\vec{F}_g\) and \(\vec{F}_r\) equal zero, then:
\[\vec{M}=\vec{r}\times\vec{F}_f = I\vec{\epsilon}\]
We rewrite to scalar form:
\[F_{f}r = I\epsilon = I \frac{a}{r}\]
The following holds for moment of inertia: \(I = mr^2\), then:
\[F_fr = mr^2\frac{a}{r}\]
Where:
\[F_f = ma\tag{2}\]
Express the acceleration of the hoop by equations (1) and (2) and then express the speed.

We substitute from (2) for F_f into equation (1):
\[mg\sin\alpha = 2ma\]
We divide expression by m:
\[a = \frac{1}{2}g\sin\alpha\tag{3}\]
The following holds for the covered distance:
\[s=\frac{1}{2}at^2\]
Where:
\[v=at\]
Where:
\[s=\frac{1}{2}a\frac{v^2}{a^2}\] \[v^2 = 2sa\] \[v=\sqrt{2sa}\]
We substitute from (4):
\[v=\sqrt{2s\frac{1}{2}g\sin\alpha}\] \[v=\sqrt{gs\sin\alpha}\]